Самый большой круг внутри невыпуклого многоугольника

Question

Как я могу найти самый большой круг, который может поместиться внутри вогнутого многоугольника?

Алгоритм грубой силы в порядке, если он может обрабатывать полигоны с ~50 вершинами в режиме реального времени.

Answer 1

Ключом к решению этой проблемы является, прежде всего, наблюдение: центр наибольшего круга, который поместится внутри произвольного многоугольника, - это точка, которая:

1. Внутри многоугольника; а также
2. Самый дальний от любой точки по краям многоугольника.

Зачем? Потому что каждая точка на краю круга равноудалена от этого центра. По определению, самый большой круг будет иметь наибольший радиус и касаться многоугольника как минимум в двух точках, поэтому, если вы найдете точку внутри самого дальнего от многоугольника, вы нашли центр круга.

Эта проблема появляется в географии и решается итеративно с любой произвольной точностью. Это называется проблема поляков недоступности. См. Полюса недоступности: алгоритм расчета для самых отдаленных мест на Земле.

Основной алгоритм работает так:

1. Определить R как прямолинейную область от (x_min, y_min) до (x_max, y_max);
2. Разделите R на произвольное количество точек. В статье в качестве эвристики используется 21 (что означает деление высоты и ширины на 20);
3. Обрезать любые точки, которые находятся за пределами многоугольника;
4. В остальном найдите точку, наиболее удаленную от любой точки на краю;
5. С этого момента определите новый R с меньшими интервалами и границами и повторите процедуру, начиная с шага 2, чтобы получить любой ответ произвольной точности. Бумага уменьшает R с коэффициентом квадратного корня из 2.

Одно замечание: как проверить, находится ли точка внутри многоугольника или нет: простейшее решение этой части проблемы - направить луч вправо от точки. Если он пересекает нечетное количество ребер, он находится внутри многоугольника. Если это четное число, оно снаружи.

Кроме того, что касается тестирования расстояния до любого ребра, необходимо рассмотреть два случая:

1. Точка перпендикулярна точке на этом ребре (в пределах границ двух вершин); или же
2. Это не так.

(2) легко. Расстояние до края - это минимум расстояний до двух вершин. Для (1) ближайшей точкой на этом ребре будет точка, которая пересекает ребро под углом 90 градусов, начиная с точки, которую вы тестируете. См. Расстояние от точки до луча или сегмента.

Answer 2

Если кто-то ищет практическую реализацию, я разработал более быстрый алгоритм, который решает эту проблему с заданной точностью, и сделал его библиотекой JavaScript. Он похож на алгоритм итеративной сетки, описанный @cletus, но он гарантирует получение глобального оптимума, а также на практике в 20-40 раз быстрее.

Проверьте это: https://github.com/mapbox/polylabel

Answer 3

Резюме: теоретически это можно сделать за O(n) раз. На практике вы можете сделать это за O(n log n) времени.

Обобщенные диаграммы Вороного.

Если вы рассматриваете вершины и ребра многоугольника как набор узлов и тесселяции внутреннего пространства в "ячейки ближайших соседей", то вы получите так называемую (обобщенную) диаграмму Вороного. Диаграмма Вороного состоит из узлов и ребер, соединяющих их. Зазор узла - это расстояние до его определяющих граней многоугольника.

(Здесь у многоугольника даже есть отверстия; принцип все еще работает.)

Ключевое наблюдение сейчас состоит в том, что центр максимального вписанного круга касается трех граней (вершин или ребер) многоугольника, и никакая другая грань не может быть ближе. Таким образом, центр должен находиться на узле Вороного, то есть узле с наибольшим зазором.

В приведенном выше примере узел, отмечающий центр максимального вписанного круга, касается двух ребер и вершины многоугольника.

Между прочим, средняя ось - это диаграмма Вороного с удаленными ребрами Вороного, исходящими из рефлекторных вершин. Следовательно, центр максимальной вписанной окружности также лежит на медиальной оси.

Источник: моя статья в блоге, которая имеет дело с обобщениями максимума вписанных кругов в некоторый момент. Там вы можете найти больше на диаграммах Вороного и их связи с максимально вписанными кругами.

Алгоритмы и реализации.

Вы могли бы фактически вычислить диаграмму Вороного. Алгоритм O(n log n) для наихудшего случая для точек и отрезков представлен Fortune, Алгоритм развёртки для диаграмм Вороного, SoCG'86. Held опубликовал программный пакет Vroni с ожидаемой O(n log n) временной сложностью, который фактически вычисляет также максимальный вписанный круг. И, кажется, есть реализация в boost тоже.

Для простых многоугольников (т. Е. Без дырок) оптимальный по времени алгоритм, который выполняется за время O(n), принадлежит Чину и др., Нахождение средней оси простого многоугольника за линейное время, 1999.

Грубая сила.

Однако, как вы заявили, что у вас все в порядке с алгоритмом грубой силы: как насчет простой проверки всех триплетов сайтов (вершин и ребер). Для каждого триплета вы найдете подходящие узлы Вороного, т. Е. Равноотстоящие локусы к трем сайтам, и проверьте, не пересекает ли какой-либо другой сайт максимально допустимый вписанный круг. Если есть пересечение, вы увольняете кандидата. Возьмите самое лучшее, что вы можете найти во всех тройнях.

См. Главу 3 в моей магистерской диссертации о более подробной информации о вычислении эквидистантных локусов для трех сайтов.

Answer 4

Алгоритм O(n log(n)):

1. Построить диаграмму Вороного из ребер в P. Это можно сделать, например, с помощью алгоритма Fortunes.
2. Для узлов Вороного (точек, равноудаленных от трех или более ребер) внутри P;
3. Найдите узел с максимальным расстоянием до ребер в P. Этот узел является центром максимального вписанного круга.

Answer 5

Я реализовал кусок кода Python, основанный на cv2, чтобы получить максимальный / самый большой вписанный круг внутри маски / многоугольника / контуров. Поддерживает невыпуклую / полую форму.

       import cv2
import numpy as np
def get_test_mask():
    # Create an image
    r = 100
    mask = np.zeros((4 * r, 4 * r), dtype=np.uint8)

    # Create a sequence of points to make a contour
    vert = [None] * 6
    vert[0] = (3 * r // 2, int(1.34 * r))
    vert[1] = (1 * r, 2 * r)
    vert[2] = (3 * r // 2, int(2.866 * r))
    vert[3] = (5 * r // 2, int(2.866 * r))
    vert[4] = (3 * r, 2 * r)
    vert[5] = (5 * r // 2, int(1.34 * r))
    # Draw it in mask
    for i in range(6):
        cv2.line(mask, vert[i], vert[(i + 1) % 6], (255), 63)
    return mask


mask = get_test_mask()

"""
Get the maximum/largest inscribed circle inside mask/polygon/contours.
Support non-convex/hollow shape
"""
dist_map = cv2.distanceTransform(mask, cv2.DIST_L2, cv2.DIST_MASK_PRECISE)
_, radius, _, center = cv2.minMaxLoc(dist_map)

result = cv2.cvtColor(mask, cv2.COLOR_GRAY2BGR)
cv2.circle(result, tuple(center), int(radius), (0, 0, 255), 2, cv2.LINE_8, 0)

# minEnclosingCircle directly by cv2
contours, _ = cv2.findContours(mask, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)[-2:]
center2, radius2 = cv2.minEnclosingCircle(np.concatenate(contours, 0))
cv2.circle(result, (int(center2[0]), int(center2[1])), int(radius2), (0, 255, 0,), 2)

cv2.imshow("mask", mask)
cv2.imshow("result", result)
cv2.waitKey(0)

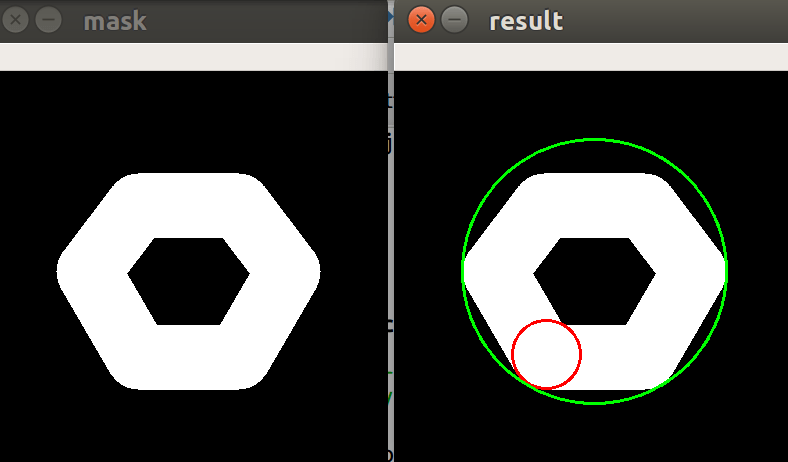
Красный круг - это максимальный вписанный круг

Источник: https://gist.github.com/DIYer22/f82dc329b27c2766b21bec4a563703cc

Answer 6

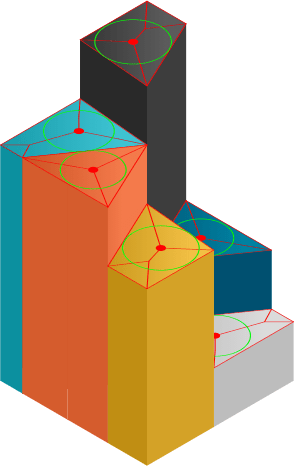
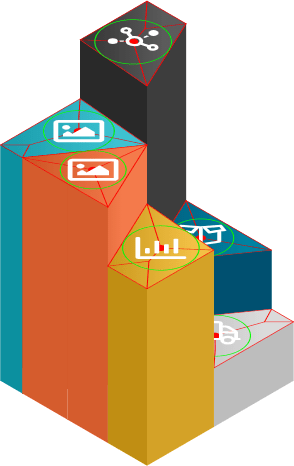
Я использовал прямые скелеты, чтобы разместить изображение внутри многоугольника в три этапа:

1. Найдите прямой скелет с помощью алгоритма прямого скелета (рис. 1).
2. На прямом каркасе найдите самый большой круг (фото 2).
3. Нарисуйте изображение внутри этого круга (фото 3).

Попробуйте: https://smart-diagram.com/diagram-designer/?template=365

Answer 7

Алгоритм O(n log X), где X зависит от требуемой точности.

Двоичный поиск наибольшего радиуса R для круга:

На каждой итерации для заданного радиуса r нажимайте каждое ребро E "внутрь" на R, чтобы получить E'. Для каждого ребра E 'определите полуплоскость H как множество всех точек "внутри" многоугольника (используя E' в качестве границы). Теперь вычислите пересечение всех этих полуплоскостей E', что можно сделать за O(n) времени. Если пересечение не пусто, то если вы нарисуете круг с радиусом r, используя любую точку на пересечении в качестве центра, он будет внутри данного многоугольника.