Повышение точности пересечения лучей и эллипсоидов
Мне нужно повысить точность работы в одном из моих шейдерных фрагментов GLSL с атмосферным рассеянием, который вычисляет пересечение между одиночным лучом и выровненным по оси эллипсоидом.
Это основная функция моего шейдера атмосферного рассеяния. Старый оригинальный шейдер был включен floats и для нормального рендеринга было хорошо, но после добавления зума я обнаружил, что при относительно небольших расстояниях точность теряется. На поплавках полезные расстояния для Земли составляли только до 0,005 а.е. (астрономическая единица). Поэтому я попытался перенести критическую функцию на double и это помогает, так что теперь полезное расстояние составляет около 1,0 а.е. (с небольшими артефактами)
Это double версия функции внутри Fragment Shader (в старом стиле используются устаревшие вещи!!!)
#extension GL_ARB_gpu_shader_fp64 : enable
double abs(double x) { if (x<0.0) x=-x; return x; }
// compute length of ray(p0,dp) to intersection with ellipsoid((0,0,0),r) -> view_depth_l0,1
// where r.x is elipsoid rx^-2, r.y = ry^-2 and r.z=rz^-2
float view_depth_l0=-1.0,view_depth_l1=-1.0;
bool _view_depth(vec3 _p0,vec3 _dp,vec3 _r)
{
double a,b,c,d,l0,l1;
dvec3 p0,dp,r;
p0=dvec3(_p0);
dp=dvec3(_dp);
r =dvec3(_r );
view_depth_l0=-1.0;
view_depth_l1=-1.0;
a=(dp.x*dp.x*r.x)
+(dp.y*dp.y*r.y)
+(dp.z*dp.z*r.z); a*=2.0;
b=(p0.x*dp.x*r.x)
+(p0.y*dp.y*r.y)
+(p0.z*dp.z*r.z); b*=2.0;
c=(p0.x*p0.x*r.x)
+(p0.y*p0.y*r.y)
+(p0.z*p0.z*r.z)-1.0;
d=((b*b)-(2.0*a*c));
if (d<0.0) return false;
d=sqrt(d);
l0=(-b+d)/a;
l1=(-b-d)/a;
if (abs(l0)>abs(l1)) { a=l0; l0=l1; l1=a; }
if (l0<0.0) { a=l0; l0=l1; l1=a; }
if (l0<0.0) return false;
view_depth_l0=float(l0);
view_depth_l1=float(l1);
return true;
}
- вход луча и радиусов ^-2 эллипсоида
выходное расстояние от р0 до пересечений
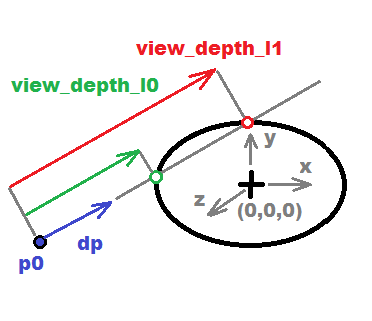
точность входных и выходных переменных float (достаточно)
Вот так это выглядит после портирования на Double

Итак, вопрос: Q1. Как повысить точность этой функции?
- целевая точность для
view_depth_l0,view_depth_l1является+/- 20 mдля расстояния|p0|=100 AU
Это было бы идеально, сейчас кажется, что +/- 5 км на расстоянии 10 AU, что плохо. Даже 10-кратное точное вычисление будет огромным шагом вперед, есть идеи?
[edit1] l0, l1 range
Я ошибся с плавающей точкой конвертации view_depth_l0,view_depth_l1 является причиной артефактов. После смещения на относительное расстояние точность значительно улучшилась. Я только добавил это:
// relative shift to preserve accuracy
const double m0=1000000000.0; // >= max view depth !!!
if (l0>m0){ a=floor(l0/m0)*m0; a-=m0; if (l1>l0) l1-=a; l0-=a; }
до этого:
view_depth_l0=float(l0);
view_depth_l1=float(l1);
return true;
}
Остальная часть шейдерной ручки l0,l1 В качестве относительных значений в любом случае получим следующее:

для расстояний до 10,0 а.е. это нормально (артефакты заметны только в очень больших масштабах), новые артефакты возникают скорее всего в других местах, поэтому мне придется продолжить исследования, когда у меня будет время и желание.
[edit2] смещение p0 вдоль dp ближе к (0,0,0)
Реализация требует относительно дорогих функций нормализации и длины, и результат без смещения диапазона (edit1) был немного лучше, чем необработанная функция, но улучшение не слишком большое. С изменением диапазона (edit1) результат тот же, что и раньше, поэтому это не так. Мой вывод заключается в том, что все оставшиеся артефакты не вызваны самой функцией просмотра.
Я попробую портировать шейдер на #version 400 + fp64 в целом, чтобы проверить, не слишком ли округлены входные данные с плавающей точкой
[edit3] фактический исходный код
#extension GL_ARB_gpu_shader_fp64 : enable
double abs(double x) { if (x<0.0) x=-x; return x; }
// compute length of ray(p0,dp) to intersection with ellipsoid((0,0,0),r) -> view_depth_l0,1
// where r.x is elipsoid rx^-2, r.y = ry^-2 and r.z=rz^-2
float view_depth_ll= 0.0, // shift to boost accuracy
view_depth_l0=-1.0, // view_depth_ll+view_depth_l0 first hit
view_depth_l1=-1.0; // view_depth_ll+view_depth_l1 second hit
const double view_depth_max=100000000.0; // > max view depth
bool _view_depth(vec3 _p0,vec3 _dp,vec3 _r)
{
dvec3 p0,dp,r;
double a,b,c,d,l0,l1;
view_depth_ll= 0.0;
view_depth_l0=-1.0;
view_depth_l1=-1.0;
// conversion to double
p0=dvec3(_p0);
dp=dvec3(_dp);
r =dvec3(_r );
// quadratic equation a.l.l+b.l+c=0; l0,l1=?;
a=(dp.x*dp.x*r.x)
+(dp.y*dp.y*r.y)
+(dp.z*dp.z*r.z);
b=(p0.x*dp.x*r.x)
+(p0.y*dp.y*r.y)
+(p0.z*dp.z*r.z); b*=2.0;
c=(p0.x*p0.x*r.x)
+(p0.y*p0.y*r.y)
+(p0.z*p0.z*r.z)-1.0;
// discriminant d=sqrt(b.b-4.a.c)
d=((b*b)-(4.0*a*c));
if (d<0.0) return false;
d=sqrt(d);
// standard solution l0,l1=(-b +/- d)/2.a
a*=2.0;
l0=(-b+d)/a;
l1=(-b-d)/a;
// alternative solution q=-0.5*(b+sign(b).d) l0=q/a; l1=c/q; (should be more accurate sometimes)
// if (b<0.0) d=-d; d=-0.5*(b+d);
// l0=d/a;
// l1=c/d;
// sort l0,l1 asc
if (abs(l0)>abs(l1)) { a=l0; l0=l1; l1=a; }
if (l0<0.0) { a=l0; l0=l1; l1=a; }
if (l0<0.0) return false;
// relative shift to preserve accuracy after conversion back float
if (l0>view_depth_max){ a=floor(l0/view_depth_max)*view_depth_max; a-=view_depth_max; view_depth_ll=float(a); if (l1>l0) l1-=a; l0-=a; }
// conversion back float
view_depth_l0=float(l0);
view_depth_l1=float(l1);
return true;
}
Портирование остальных шейдеров на удвоение не имеет никакого эффекта. Единственное, что могло бы улучшить это double входные данные (вход double но GL преобразовать его в float), но мой нынешний GLSL HW не позволяет 64 bit интерполяторы
Q2. Есть ли способ пройти double интерполяторы из вершины в фрагментный шейдер?
Что-то вроде varying dvec4 pixel_pos; в старом стиле GLSL или out smooth dvec4 pixel_pos; в профиле ядра