Вычисление позы камеры с матрицей гомографии на основе 4 копланарных точек
У меня есть 4 копланарных точки в видео (или изображении), представляющих квад (не обязательно квадрат или прямоугольник), и я хотел бы иметь возможность отображать виртуальный куб поверх них, где углы куба стоят точно по углам видео квадроцикл.
Поскольку точки копланарны, я могу вычислить гомографию между углами единичного квадрата (то есть [0,0] [0,1] [1,0] [1,1]) и видео координатами квадратора.
Из этой гомографии я должен быть в состоянии вычислить правильную позу камеры, то есть [R|t], где R - это матрица вращения 3x3, а t - вектор трансляции 3x1, так что виртуальный куб лежит на видеокадре.
Я прочитал много решений (некоторые из них на SO) и попытался реализовать их, но они, кажется, работают только в некоторых "простых" случаях (например, когда квадратик видео является квадратом), но не работают в большинстве случаев.
Вот методы, которые я попробовал (большинство из них основаны на одних и тех же принципах, только вычисления перевода немного отличаются). Пусть K - матрица внутренних характеристик камеры, а H - гомография. Мы вычисляем:
A = K-1 * H
Пусть a1,a2,a3 - векторы столбцов A, а r1,r2,r3 - векторы столбцов матрицы вращения R.
r1 = a1 / ||a1||
r2 = a2 / ||a2||
r3 = r1 x r2
t = a3 / sqrt(||a1||*||a2||)
Проблема в том, что это не работает в большинстве случаев. Чтобы проверить мои результаты, я сравнил R и t с результатами, полученными с помощью метода executePnP OpenCV (используя следующие трехмерные точки [0,0,0] [0,1,0] [1,0,0] [1,1,0]).
Так как я отображаю куб одинаково, я заметил, что в каждом случае solvePnP дает правильные результаты, в то время как поза, полученная из гомографии, в основном неверна.
Теоретически, поскольку мои точки копланарны, можно вычислить позу по омографии, но я не смог найти правильный способ вычисления позы из H.
Любое понимание того, что я делаю неправильно?
Редактировать после попытки метода @Jav_Rock
Привет, Jav_Rock, большое спасибо за твой ответ, я попробовал твой подход (и многие другие), который кажется более или менее нормальным. Тем не менее, у меня все еще есть некоторые проблемы при вычислении позы, основанной на 4 копланарной точке. Чтобы проверить результаты, я сравниваю их с результатами solvePnP (что будет намного лучше благодаря подходу минимизации ошибок повторного проецирования).
Вот пример:
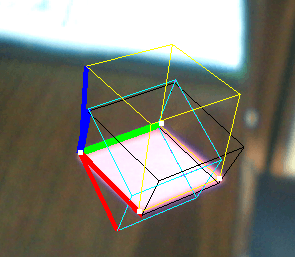
- Желтый куб: Решить ПНП
- Черный куб: техника Jav_Rock
- Голубой (и фиолетовый) куб (ы): некоторые другие методы дают те же результаты
Как вы можете видеть, черный куб более или менее в порядке, но не выглядит пропорционально, хотя векторы кажутся ортонормированными.
РЕДАКТИРОВАТЬ 2: Я нормализовал v3 после его вычисления (для обеспечения ортонормированности), и, похоже, это также решает некоторые проблемы.
7 ответов
Если у вас есть гомография, вы можете рассчитать позу камеры следующим образом:
void cameraPoseFromHomography(const Mat& H, Mat& pose)
{
pose = Mat::eye(3, 4, CV_32FC1); // 3x4 matrix, the camera pose
float norm1 = (float)norm(H.col(0));
float norm2 = (float)norm(H.col(1));
float tnorm = (norm1 + norm2) / 2.0f; // Normalization value
Mat p1 = H.col(0); // Pointer to first column of H
Mat p2 = pose.col(0); // Pointer to first column of pose (empty)
cv::normalize(p1, p2); // Normalize the rotation, and copies the column to pose
p1 = H.col(1); // Pointer to second column of H
p2 = pose.col(1); // Pointer to second column of pose (empty)
cv::normalize(p1, p2); // Normalize the rotation and copies the column to pose
p1 = pose.col(0);
p2 = pose.col(1);
Mat p3 = p1.cross(p2); // Computes the cross-product of p1 and p2
Mat c2 = pose.col(2); // Pointer to third column of pose
p3.copyTo(c2); // Third column is the crossproduct of columns one and two
pose.col(3) = H.col(2) / tnorm; //vector t [R|t] is the last column of pose
}
Этот метод работает от меня. Удачи.
Ответ, предложенный Jav_Rock, не обеспечивает правильное решение для позы камеры в трехмерном пространстве.
Для оценки трехмерного преобразования и поворота, вызванного гомографией, существует несколько подходов. Одна из них предоставляет закрытые формулы для разложения гомографии, но они очень сложны. Кроме того, решения никогда не бывают уникальными.
К счастью, OpenCV 3 уже реализует эту декомпозицию ( degposeHomographyMat). Учитывая гомографию и правильно масштабированную встроенную матрицу, функция обеспечивает набор из четырех возможных поворотов и переносов.
На всякий случай кому-нибудь понадобится портирование на python функции, написанной @Jav_Rock:
def cameraPoseFromHomography(H):
H1 = H[:, 0]
H2 = H[:, 1]
H3 = np.cross(H1, H2)
norm1 = np.linalg.norm(H1)
norm2 = np.linalg.norm(H2)
tnorm = (norm1 + norm2) / 2.0;
T = H[:, 2] / tnorm
return np.mat([H1, H2, H3, T])
Хорошо работает в моих задачах.
Вычисление [R|T] из матрицы гомографии немного сложнее, чем ответ Jav_Rock.
В OpenCV 3.0 есть метод cv::degposeHomographyMat, который возвращает четыре потенциальных решения, одно из которых правильное. Однако OpenCV не предоставил способ выбрать правильный.
Сейчас я работаю над этим и, возможно, опубликую свои коды здесь позже в этом месяце.
Самолет, на котором изображен ваш Квадрат на изображении, имеет в своем составе исчезающие дорожки. Уравнение этой линии: Ax + B y + C = 0.
Нормой вашего самолета является (A,B,C)!
Пусть p00, p01, p10, p11 - координаты точки после применения внутренних параметров камеры и в однородной форме, например, p00=(x00,y00,1)
Линия исчезновения может быть рассчитана как:
- вниз = p00 кросс p01;
- слева = р00 крест р10;
- справа = р01 крест р11;
- вверх = р10 крест р11;
- v1 = левый крест вправо;
- v2 = вверх крест вниз;
- vanish_line = v1 пересечь v2;
Где крестик в стандартном векторном перекрестном произведении
Вы можете использовать эту функцию. Работает на меня.
def find_pose_from_homography(H, K):
'''
function for pose prediction of the camera from the homography matrix, given the intrinsics
:param H(np.array): size(3x3) homography matrix
:param K(np.array): size(3x3) intrinsics of camera
:Return t: size (3 x 1) vector of the translation of the transformation
:Return R: size (3 x 3) matrix of the rotation of the transformation (orthogonal matrix)
'''
#to disambiguate two rotation marices corresponding to the translation matrices (t and -t),
#multiply H by the sign of the z-comp on the t-matrix to enforce the contraint that z-compoment of point
#in-front must be positive and thus obtain a unique rotational matrix
H=H*np.sign(H[2,2])
h1,h2,h3 = H[:,0].reshape(-1,1), H[:,1].reshape(-1,1) , H[:,2].reshape(-1,1)
R_ = np.hstack((h1,h2,np.cross(h1,h2,axis=0))).reshape(3,3)
U, S, V = np.linalg.svd(R_)
R = U@np.array([[1,0,0],
[0,1,0],
[0,0,np.linalg.det(U@V.T)]])@V.T
t = (h3/np.linalg.norm(h1)).reshape(-1,1)
return R,t
Вот версия Python, основанная на версии, предоставленной Дмитрием Волошиным, которая нормализует матрицу вращения и переносит результат в 3x4.
def cameraPoseFromHomography(H):
norm1 = np.linalg.norm(H[:, 0])
norm2 = np.linalg.norm(H[:, 1])
tnorm = (norm1 + norm2) / 2.0;
H1 = H[:, 0] / norm1
H2 = H[:, 1] / norm2
H3 = np.cross(H1, H2)
T = H[:, 2] / tnorm
return np.array([H1, H2, H3, T]).transpose()