Создать вектор полных чебышевских полиномов от Юлии (или MATLAB)?

Question

Предположим, что у нас есть двумерная функция f(x,y), которую мы хотим аппроксимировать множеством полиномов Чебышева до степени 2. Пусть полином Чебышева степени j равен T_j(x) или T_j(y). Обычно мы приближаем f(x,y), строя функцию g(x,y), которая является тензорным произведением одномерных полиномов,

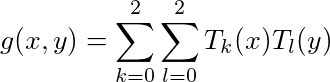
Я хочу создать полный многочлен Чебышева уровня N. Это как раз тензорное произведение, как и выше, но где сумма индексов k+l должна быть меньше или равна N. Так что, если N было 3, тогда у нас были бы все члены в вышеприведенной сумме, кроме T₂(x) * T₂(y), так как 2+2=4 > 3. По мере увеличения размерности функции теряется много других членов.

В конечном итоге я хотел бы сделать это с гибким выбором уровня и без необходимости выписывать кучу вложенных циклов, если я работаю с более чем 2 или 3 измерениями. Это похоже на @nloops был бы способ пойти, но я не могу понять это.

Например, предположим, что я хочу оценить 2-мерный полином Чебышева в точке (.5,.5). Я могу написать встроенную функцию, которая возвращает одномерный полином Чебышева уровня N в точке x.

cheb(d,x) = cos((d)*acos(x))
a = [.5, .5]
polys1d = [cheb(d,a[i]) for d = 0:2, i = 1:length(a)]

Создать полный многочлен тензорного произведения в двух измерениях (или даже больше) легко. Например:

polys2d = kron(polys1d[:,1],polys1d[:,2])

Но создание полного полинома в общем случае немного сложнее. Я хотел бы, чтобы это было сделано так, чтобы я не начинал с построения полного тензорного произведения, а затем удалял многочлены, в которых сумма степеней больше уровня. Это займет много памяти, если количество измерений и уровень будут большими.

Answer 1

Если мы определим следующую вспомогательную функцию:

using Iterators   # install with Pkg.add("Iterators")

nlimitedkparts(n,k) = (diff([0;v]).-1 for v in subsets(1:(n+k),k))

Мы можем сгенерировать следующее:

julia> ["T_$(r[1])(x)*T_$(r[2])(y)" for r in nlimitedkparts(3,2)]
10-element Array{String,1}:
 "T_0(x)*T_0(y)"
 "T_0(x)*T_1(y)"
 "T_0(x)*T_2(y)"
 "T_0(x)*T_3(y)"
 "T_1(x)*T_0(y)"
 "T_1(x)*T_1(y)"
 "T_1(x)*T_2(y)"
 "T_2(x)*T_0(y)"
 "T_2(x)*T_1(y)"
 "T_3(x)*T_0(y)"

Конечно, вы можете захотеть сделать что-то еще, кроме генерации этих строк, но с использованием того же nlimitedkparts функция.