Фитинг с Монте-Карло в питоне

Question

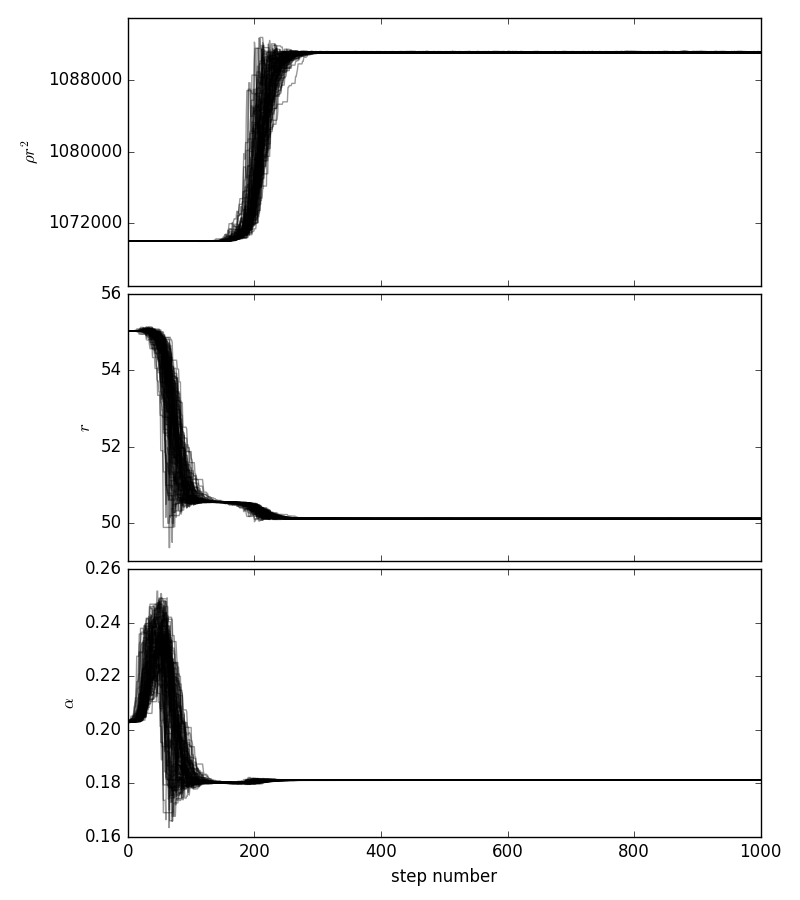
Я использую пакет Python под названием emcee чтобы приспособить функцию к некоторым точкам данных. Подгонка выглядит отлично, но когда я хочу построить значение каждого параметра на каждом шаге, я получаю это:

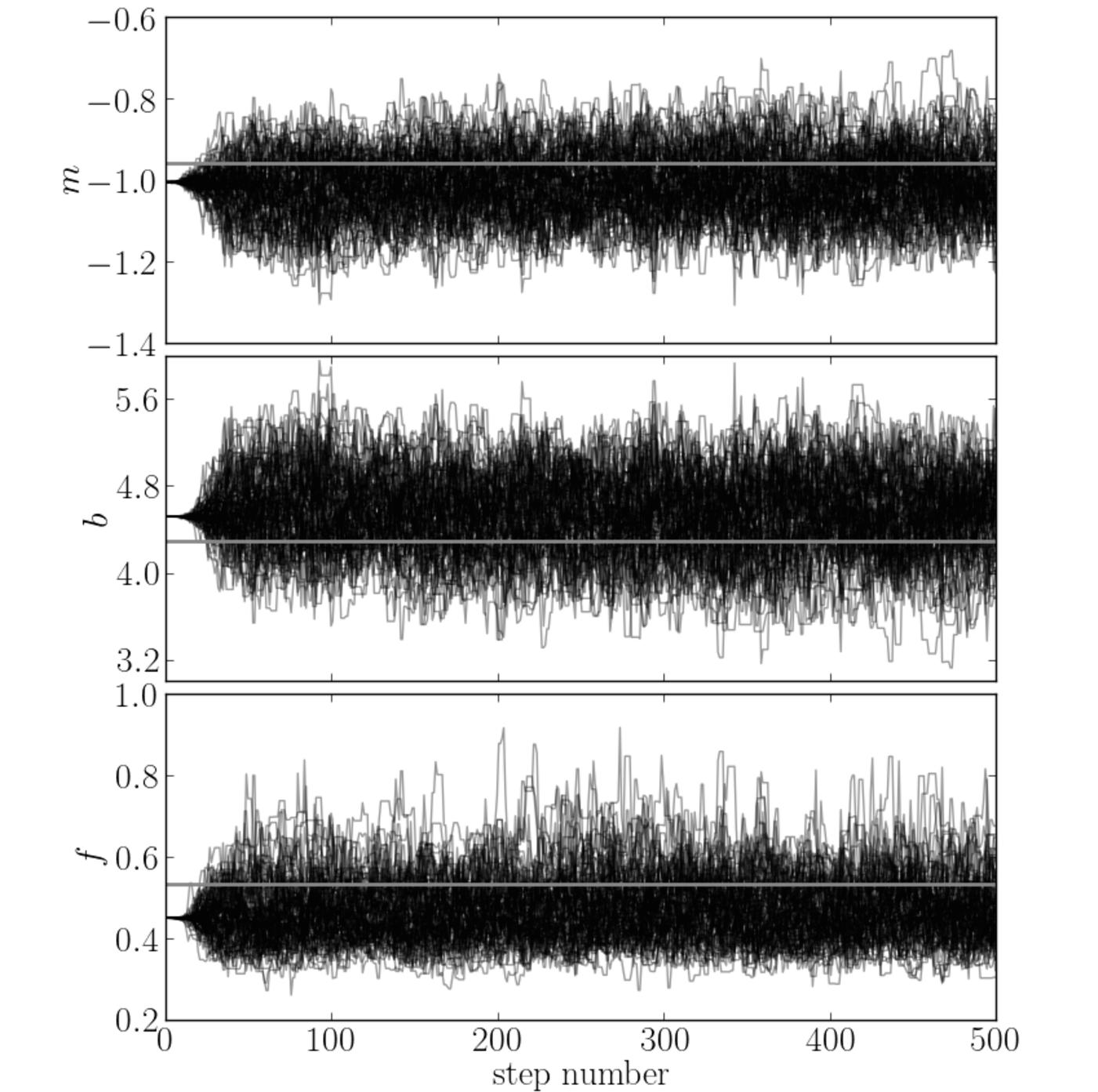
В их примере (с другой функцией и точками данных) они получают это:

Почему моя функция сходится так быстро, и почему она имеет такую ​​странную форму в начале. Я применяю MCMC, используя вероятность и апостериорную вероятность. И даже если подгонка выглядит очень хорошо, ошибки в параметрах функции очень малы (на 10^10 меньше, чем фактическое значение), и я думаю, что это из-за случайных блужданий. Есть идеи как это исправить? Вот их код для подгонки: http://dan.iel.fm/emcee/current/user/line/ Я использовал тот же код с очевидными модификациями для моих точек данных и функции подгонки.

Answer 1

Я бы не сказал, что ваша функция сходится быстрее, чем emcee пример линии, с которой вы связаны. В этом примере обходчики начинают изучать наиболее вероятные значения в пространстве параметров почти сразу, тогда как в вашем случае для достижения области высокой вероятности требуется более 200 итераций.

Скачок в ваших графиках трассировки выглядит как выжигание. Это общая особенность алгоритмов выборки MCMC, когда вашим ходячим дают отправные точки вдали от задней части тела, а затем они должны найти путь к нему. Похоже, что в вашем случае функция правдоподобия довольно плавная, поэтому вам нужно всего лишь около ста итераций, чтобы добиться этого, придавая вашей функции ту "странную форму", о которой вы говорите.

Если вы можете лучше ограничить начальные точки, сделайте это; если нет, вы можете рассмотреть возможность отбросить эту начальную длину до того, как будет проведен дальнейший анализ (см. здесь и здесь, чтобы обсудить увеличение длины).

Что касается того, являются ли ошибки реалистичными или нет, вам необходимо проверить получающиеся апостериорные модели для этого, потому что отношение фактического значения параметра к его неопределенностям не имеет права голоса в этом. Например, если мы возьмем ваш связанный пример и изменим истинное значение b до 10^10, итоговые ошибки будут на десять величин меньше, оставаясь при этом совершенно достоверными.