R: построение апостериорных вероятностей классификации линейного дискриминантного анализа в ggplot2

Question

С помощью ggord можно провести хороший линейный дискриминантный анализ ggplot2 биплоты (см. главу 11, рис. 11.5 в книге "Биплоты на практике" М. Гринакра), как в

library(MASS)
install.packages("devtools")
library(devtools)
install_github("fawda123/ggord")
library(ggord)
data(iris)
ord <- lda(Species ~ ., iris, prior = rep(1, 3)/3)
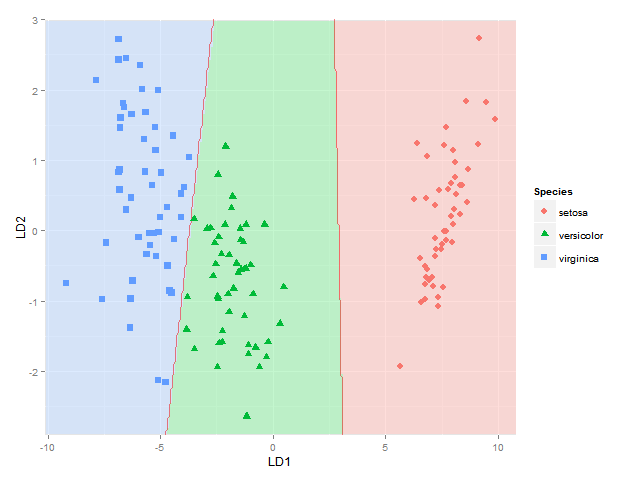
ggord(ord, iris$Species)

Я также хотел бы добавить области классификации (показанные как сплошные области того же цвета, что и их соответствующая группа, скажем, альфа =0,5) или апостериорные вероятности принадлежности к классу (при этом альфа изменяется в зависимости от этой апостериорной вероятности и того же цвета, что и используется для каждой группы) (как это можно сделать в BiplotGUI, но я ищу ggplot2 решение). Кто-нибудь знает, как это сделать с ggplot2возможно используя geom_tile?

РЕДАКТИРОВАТЬ: ниже кто-то спрашивает, как рассчитать апостериорные вероятности классификации и прогнозируемые классы. Это выглядит так:

library(MASS)
library(ggplot2)
library(scales)
fit <- lda(Species ~ ., data = iris, prior = rep(1, 3)/3)
datPred <- data.frame(Species=predict(fit)$class,predict(fit)$x)
#Create decision boundaries
fit2 <- lda(Species ~ LD1 + LD2, data=datPred, prior = rep(1, 3)/3)
ld1lim <- expand_range(c(min(datPred$LD1),max(datPred$LD1)),mul=0.05)
ld2lim <- expand_range(c(min(datPred$LD2),max(datPred$LD2)),mul=0.05)
ld1 <- seq(ld1lim[[1]], ld1lim[[2]], length.out=300)
ld2 <- seq(ld2lim[[1]], ld1lim[[2]], length.out=300)
newdat <- expand.grid(list(LD1=ld1,LD2=ld2))
preds <-predict(fit2,newdata=newdat)
predclass <- preds$class
postprob <- preds$posterior
df <- data.frame(x=newdat$LD1, y=newdat$LD2, class=predclass)
df$classnum <- as.numeric(df$class)
df <- cbind(df,postprob)
head(df)

           x        y     class classnum       setosa   versicolor virginica
1 -10.122541 -2.91246 virginica        3 5.417906e-66 1.805470e-10         1
2 -10.052563 -2.91246 virginica        3 1.428691e-65 2.418658e-10         1
3  -9.982585 -2.91246 virginica        3 3.767428e-65 3.240102e-10         1
4  -9.912606 -2.91246 virginica        3 9.934630e-65 4.340531e-10         1
5  -9.842628 -2.91246 virginica        3 2.619741e-64 5.814697e-10         1
6  -9.772650 -2.91246 virginica        3 6.908204e-64 7.789531e-10         1

colorfun <- function(n,l=65,c=100) { hues = seq(15, 375, length=n+1); hcl(h=hues, l=l, c=c)[1:n] } # default ggplot2 colours
colors <- colorfun(3)
colorslight <- colorfun(3,l=90,c=50)
ggplot(datPred, aes(x=LD1, y=LD2) ) +
    geom_raster(data=df, aes(x=x, y=y, fill = factor(class)),alpha=0.7,show_guide=FALSE) +
    geom_contour(data=df, aes(x=x, y=y, z=classnum), colour="red2", alpha=0.5, breaks=c(1.5,2.5)) +
    geom_point(data = datPred, size = 3, aes(pch = Species,  colour=Species)) +
    scale_x_continuous(limits = ld1lim, expand=c(0,0)) +
    scale_y_continuous(limits = ld2lim, expand=c(0,0)) +
    scale_fill_manual(values=colorslight,guide=F)

(ну не совсем уверен, что этот подход для отображения границ классификации с использованием контуров / разрывов на 1,5 и 2,5 всегда верен - он корректен для границы между видами 1 и 2 и видами 2 и 3, но не в том случае, если область вида 1 будет рядом с видом 3, так как тогда я получил бы две границы - возможно, мне пришлось бы использовать подход, использованный здесь, где каждая граница между каждой парой видов рассматривается отдельно)

Это дает мне возможность составлять графики областей классификации. Я ищу решение, хотя бы также построить фактические вероятностные вероятности классификации для каждого вида по каждой координате, используя альфа (непрозрачность), пропорциональную апостериорной вероятности классификации для каждого вида, и цвет для конкретного вида. Другими словами, со стеком из трех изображений накладывается. Поскольку альфа-смешение в ggplot2, как известно , зависит от порядка, я думаю, что цвета этого стека должны быть рассчитаны заранее, и построены с использованием чего-то вроде

qplot(x, y, data=mydata, fill=rgb, geom="raster") + scale_fill_identity() 

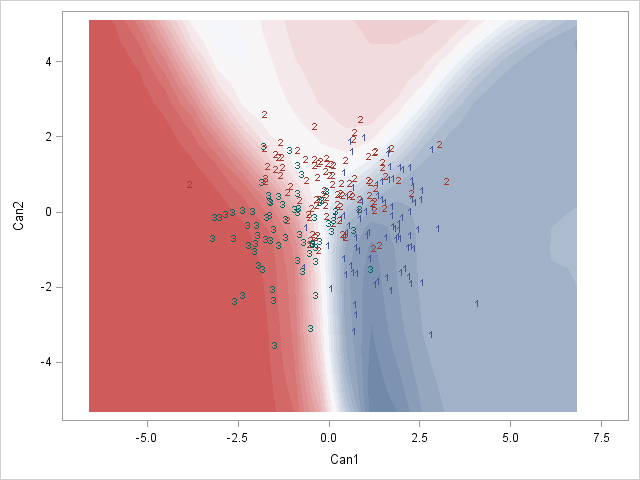
Вот пример SAS того, что я после:

Кто-нибудь знает, как это сделать? Или у кого-нибудь есть мысли о том, как лучше всего представить эти апостериорные вероятности классификации?

Обратите внимание, что метод должен работать для любого количества групп, а не только для этого конкретного примера.

Answer 1

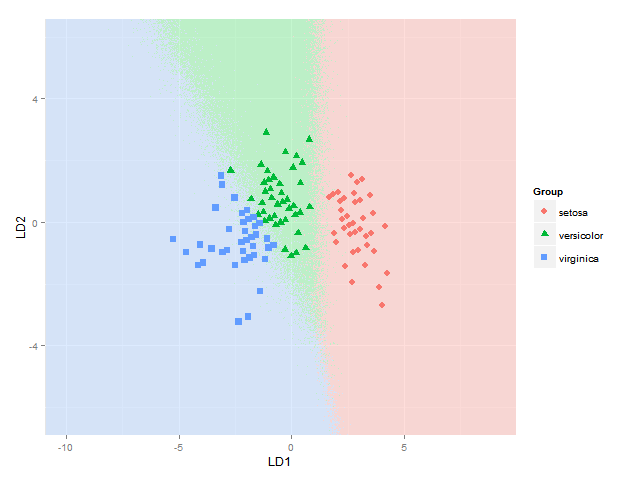
Также просто придумал следующее простое решение: просто сделать колонку в df где классовые прогнозы делаются стохастически, в соответствии с апостериорными вероятностями, что затем приводит к размыванию в неопределенных областях, например, в

fit = lda(Species ~ Sepal.Length + Sepal.Width, data = iris, prior = rep(1, 3)/3)
ld1lim <- expand_range(c(min(datPred$LD1),max(datPred$LD1)),mul=0.5)
ld2lim <- expand_range(c(min(datPred$LD2),max(datPred$LD2)),mul=0.5)

отдых, как указано выше, и вставка

lvls=unique(df$class)
df$classpprob=apply(df[,as.character(lvls)],1,function(row) sample(lvls,1,prob=row))

p=ggplot(datPred, aes(x=LD1, y=LD2) ) +
  geom_raster(data=df, aes(x=x, y=y, fill = factor(classpprob)),hpad=0, vpad=0, alpha=0.7,show_guide=FALSE) +
  geom_point(data = datPred, size = 3, aes(pch = Group,  colour=Group)) +
  scale_fill_manual(values=colorslight,guide=F) +
  scale_x_continuous(limits=rngs[[1]], expand=c(0,0)) +
  scale_y_continuous(limits=rngs[[2]], expand=c(0,0))

дает мне

Гораздо проще и понятнее, чем начинать смешивать цвета каким-то аддитивным или вычитающим образом (в той части, где у меня все еще были проблемы, и которая, видимо, не так проста, чтобы преуспеть).

Answer 2

Я полагаю, что самым простым способом будет показать апостериорные вероятности. Это довольно просто для вашего случая:

datPred$maxProb <- apply(predict(fit)$posterior, 1, max)
ggplot(datPred, aes(x=LD1, y=LD2) ) +
  geom_raster(data=df, aes(x=x, y=y, fill = factor(class)),alpha=0.7,show_guide=FALSE) +
  geom_contour(data=df, aes(x=x, y=y, z=classnum), colour="red2", alpha=0.5, breaks=c(1.5,2.5)) +
  geom_point(data = datPred, size = 3, aes(pch = Species,  colour=Species, alpha = maxProb)) +
  scale_x_continuous(limits = ld1lim, expand=c(0,0)) +
  scale_y_continuous(limits = ld2lim, expand=c(0,0)) +
  scale_fill_manual(values=colorslight, guide=F)

Вы можете видеть точки, сливающиеся на сине-зеленой границе.