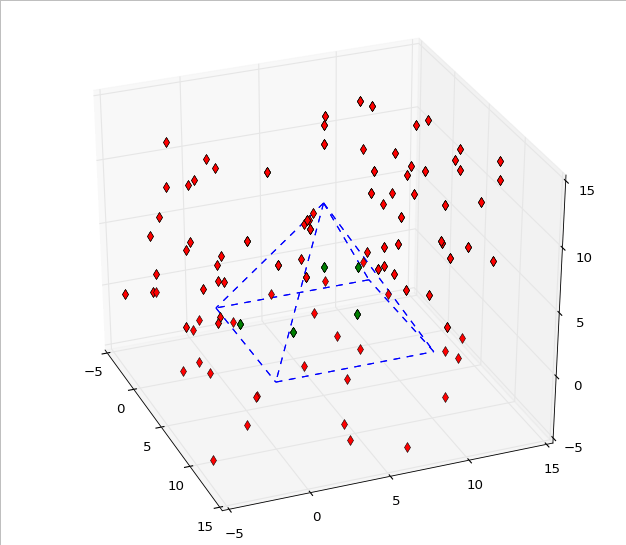
Алгоритм проверки, находится ли 3D-точка внутри выпуклого многогранника (квадратная пирамида)
Я искал надежные алгоритмы обнаружения столкновений и нашел потрясающую книгу Кристера Эриксона " Обнаружение столкновений в реальном времени ". Я пытаюсь использовать конкретный алгоритм, который проверяет, находится ли заданная точка внутри выпуклого многогранника (в трехмерном пространстве это квадратная пирамида, куб и тетраэдр (он же пирамида со всеми сторонами в виде треугольника)). В моем случае у меня квадратная пирамида. Проверка правильности точки выполняется с использованием объема пересечения для заданного числа полупространств и определения того, находится ли точка впереди или позади всех плоскостей, охватываемых сторонами многогранника. У меня трудности с пониманием использования аргумента n (см. ниже), которое представляет число полупространств для данного многогранника:
// Test if point p inside polyhedron given as the intersection volume of n halfspaces
int TestPointPolyhedron(Point p, Plane *h, int n) {
for (int i = 0; i < n; i++) {
if(DistPointPlane(p, h[i]) > 0.0f) return 0;
}
return 1;
}
с DistPointPlane(...) вычисление расстояния между заданной точкой и плоскостью
float DistPointPlane(Point q, Plane p) {
return Dot(q, p.n) - p.d;
}
а также Plane будучи структурой, которая представляет плоскость в трехмерном пространстве
struct Plane {
Vector n; // Plane normal. Point X on the plane satisfies Dot(n, X) = d
float d; // d = dot(n, p) for a given point on the plane
}
Plane ComputePlane(Point a, Point b, Point c) {
Plane p;
p.n = Normalize(Cross(b - a, c - a));
p.d = Dot(p.n, a);
return p;
}
Что алгоритм делает в основном следующее:
- Для заданной точки рассчитайте ее расстояние до каждой плоскости выпуклого многогранника
- Проверьте, является ли расстояние отрицательным или положительным
- Если расстояние отрицательное, точка лежит на противоположной стороне от нормали плоскости, поэтому она находится позади нее.
- Еще одна точка лежит на той же стороне, что и самолет в норме, поэтому она находится перед ним
- Если точка находится позади всех плоскостей данного многогранника, она лежит внутри, иначе она лежит снаружи
Теперь в терминах квадратной пирамиды, насколько я могу судить, существует 10 полупространств, поскольку у нас есть 4 стороны и основание, представляющее отдельную плоскость (то есть всего 5 плоскостей), которая делит трехмерное пространство на два полупространства (5 planes * 2 = 10 halfspaces). То, что я не понимаю, это использование n в коде для алгоритма выше. Он используется в качестве условия завершения цикла, который проходит через массив Plane экземпляров. Однако, как уже упоминалось, есть 10 полупространств.
Одна вещь, о которой я подумал после некоторого рытья, это то, что пересечение между двумя плоскостями - это линия (край пирамиды). Дальнейшее цитирование Wolfram Mathworld
Чтобы однозначно указать линию, необходимо также найти определенную точку на ней. Это можно определить, найдя точку, находящуюся одновременно на обеих плоскостях.
Каждая из вершин пирамиды удовлетворяет этому требованию, поскольку для любых заданных двух сторон (включая основание) мы получаем линию, которая находится между двумя вершинами пирамиды. Таким образом, с точки зрения пересечения у нас есть 5 (4 для основания и 1 для вершины), однако текст в книге (включая комментарий над реализацией функции) является расплывчатым, и, читая его, можно получить неверное представление (по крайней мере, это мое дело).
Моё мышление близко к истине или я упускаю какой-то большой кусок с точки зрения математических знаний?
Я перенес код на Python 3 и изменил алгоритм, чтобы циклически проходить только мой список плоскостей без дополнительного аргумента (который, если мои мысли верны, в основном такой же, как и исходный), и построил его с помощью matplotlib, Это прекрасно работает, но я все еще хочу знать, правильно ли я это понял или нет:
2 ответа
По сути, ваша фигура - это многогранник, но она просто определяется как фигура с несколькими гранями, обычно 6. Вам действительно нужно искать имя тетраэдр, которое является классической формой пирамиды, которую вы определили в визуальном представлении выше. Но основной ответ - взять нормаль к пяти вашим плоскостям (4 треугольника и один квадрат) и проверить, направлены ли они в одном направлении с точкой в пространстве. Если они все возвращают false, то ваша точка находится внутри фигуры. Если какой-либо из них вернет true, значит, вы находитесь за пределами фигуры. Этот тип теста работает для большинства выпуклых форм, потому что нет ни одного случая, когда плоскости перекрывают там нормали.
Я бы сказал, что вы поняли большую часть этого. Я не уверен, что именно вы имеете в виду под "расстоянием". Обычно dotproduct обеспечивает угол между двумя векторами. В вашем случае есть один вектор положения (точка) и один вектор нормали. Из-за законов косинуса, если точечный продукт больше 0, угол между двумя векторами составляет менее 90 градусов. С другой стороны, если продукт отрицательный, угол больше 90 градусов. Если это 0, векторы ортогональны. Так что в основном это не имеет ничего общего с расстоянием, но с углами.