Триангуляция монотонного многоугольника с коллинеарными вертикальными краевыми сегментами

Question

Я пытаюсь реализовать триангуляцию полигонов, используя широко известный алгоритм двухпроходной линии развертки, который делит многоугольник на монотонные подкомпоненты в первом проходе линии развертки, а затем триангулирует эти монотонные компоненты во втором проходе. Моя текущая реализация работает для общего случая, но я не могу понять, как ее адаптировать для работы с входными данными, содержащими несколько совпадающих краевых сегментов (сегменты с равными x-координатами при перемещении слева направо, или равные y-координаты при движении справа налево).

Редактировать: я только что понял, что то, как я сформулировал этот вопрос, делает его довольно длинным и многословным, так что вот быстрый TL;DR; для тех, кто знает о полигональной триангуляции, но не хочет читать все целиком: является ли следующая форма допустимым входным сигналом для 2-го прохода алгоритма триангуляции? Если да: как адаптировать второй проход для обработки, если нет: как адаптировать 1-й проход таким образом, чтобы он генерировал монотонные подкомпоненты, которые можно подавать во 2-й проход:

http://www.wouterbijlsma.nl/~wouter/tmp/RTdr6rET9.png

Длинная версия вопроса ниже этого пункта;-)

Очень краткое изложение алгоритма:

1. Первый проход делит входной многоугольник на "монотонные подкомпоненты". Монотонный подкомпонент - это многоугольник, который можно разбить на 2 соединенных цепочки, координаты которых отсортированы либо слева направо (если алгоритм реализован с использованием вертикальной линии развертки), либо сверху вниз (при использовании горизонтальной развертки линия). Давайте предположим, что мы используем вертикальную линию развертки: каждый монотонный подкомпонент может быть затем разбит на верхнюю цепочку и нижнюю цепочку, соединенные в минимальной и максимальной x-координатах, а при сканировании вершин любой из цепей x-координаты растет. Если подкомпонент строго мононтонный, верхняя и нижняя цепочки не могут иметь краевые сегменты с одинаковыми x-координатами (то есть: вертикальные краевые сегменты).

2. Второй проход подметает монотонные подкомпоненты и делит их на треугольники, добавляя внутренние ребра. Идея состоит в том, что каждый подкомпонент перемещается слева направо, и в каждой вершине, пораженной линией развертки, может произойти одно из двух: а) нетриангулированная область слева от линии развертки может быть триангулирована путем добавления диагоналей, или b) текущая вершина не может "видеть" ни одну из ранее пройденных, но необработанных вершин в нетриангулированной области слева от линии развертки. В случае b) вершина помещается в стек ("цепочка рефлексов"), и по построению в некоторой точке будет иметь место случай а), и вершины цепочки рефлексов будут выталкиваться один за другим и соединяться с диагонали до последней вершины линии развертки.

В приведенном выше описании отсутствуют некоторые детали, но я бы предположил, что любой, кто знает, как ответить на мой вопрос, уже понимает алгоритм, поэтому я не буду вдаваться в подробности.

У меня проблема в следующем: предположим, у меня есть многоугольник, представляющий стрелку, которая указывает влево, например, вот так:

http://www.wouterbijlsma.nl/~wouter/tmp/RTdr6rET9.png

Когда я ввожу эту форму в свой алгоритм, проход монотонного подразделения оставляет форму нетронутой: в ней есть вертикальные ребра, поэтому она не является строго монотонной, но является монотонной, и, насколько я понимаю, алгоритм не должен быть разделенным, прежде чем вы сможете триангулировать его (возможно, именно здесь я ошибаюсь, потому что мое предположение неверно).

Теперь предположим, что я подаю (неизмененный) многоугольник со стрелкой во второй проход, чтобы триангулировать его. Как мне разобраться с 2 вертикальными краевыми сегментами в основании наконечника стрелки? Алгоритм развертки требует, чтобы вершины многоугольника сортировались слева направо, поэтому можно предположить, что ответ сводится к тому, как отсортировать вершины с одинаковыми координатами x (например, в порядке цепочки, или по координате y, или на граничный индекс многоугольника), но какую бы сортировку я ни использовал, триангуляция всегда будет неудачной.

Давайте назовем самую левую вершину вершиной 0 и упорядочим вершины против часовой стрелки. Это означает, что 4 вершины основания стрелки являются вершинами 1, 2, 5 и 6. У нас есть три варианта сортировки:

1. В некотором исходном материале, который я использовал для реализации алгоритма, написано: "сортировать вершины с равными координатами x при увеличении координат y, т. Е. 1, 2, 5, 6. Если я сделаю это и разверну их, первый треугольник получится нормальным (0, 1, 2), но после этого алгоритм добавит ребро (5, 2), которое создает 4-вершинный компонент (0, 2, 5, 6). Ребро (0, 5) не добавляется, потому что алгоритм триангуляции предписывает добавлять ребра во все предыдущие нетриангулированные вершины в цепочке рефлексов, кроме первой (изменение этого приведет к нарушению общего случая). Хотя область многоугольника, ограниченная четырьмя вершинами, имеет треугольную форму, она, очевидно, не является треугольником, поскольку имеет 4 точки, и в большинстве определений она также недопустима, поскольку имеет коллинеарные ребра.

2. В другой статье, которую я прочитал, говорится: "Разорви связи, чтобы порядок цепочек сохранялся" Это означало бы, что 4 вершины в моем примере будут отсортированы в 1, 2, 6, 5, так как нижняя и верхняя цепочки идут слева направо. Если я разверну их в этом порядке, я снова получу треугольник (0, 1, 2), но следующая сканированная вершина (6) создаст многоугольник (0, 1, 6), что даже хуже, чем в первом случае, потому что он создает ребро (1, 6), которое проходит по вершине 5, но не содержит его. Широкая вершина 5 полностью испортит состояние алгоритма, потому что она создаст вырожденный треугольник (1, 5, 6), линию, а чистая вершина хвоста не сможет триангулировать оставшуюся часть многоугольника.

3. Сортировка по исходному порядку вершин многоугольника (вдоль границы, против часовой стрелки): в этом случае это даст тот же результат, что и в случае 1), то есть: 1, 2, 5, 6, который, как уже было показано, потерпел неудачу.

Я начинаю думать, что, возможно, форму стрелки, подобную этой, следует считать немонотонной, или (хотя я никогда не видел этого в каком-либо описании алгоритма) алгоритм монотонной триангуляции требует, чтобы входные данные были строго монотонными. Может быть, это то, чего мне не хватает? И если да, как мне нужно адаптировать монотонный проход подразделения для работы с (множественными, совпадающими) вертикальными краевыми сегментами? Исходный материал, который я использовал, классифицирует все вершины как "начало", "конец", "объединение", "разделение" или "обычный" (нижний / верхний) во время подразделения, но в случае вертикального сегмента эти классификации неоднозначны: в соответствии с согласно определению этих классов вершин, вершинная часть вертикального сегмента могла бы рассматриваться как начальная / конечная вершина, но также как вершина расщепления или слияния. Или, может быть, мне нужно отсортировать 4 вершины по их y-координатам, затем создать недопустимый компонент треугольника с 4 вершинами с 2 коллинеарными ребрами, а затем "исправить это", удалив вершину на коллинеарных ребрах?

Основным источником, который я использовал для реализации этого алгоритма, является оригинальная статья GJPT-78, в которой был представлен алгоритм триангуляции, он не является общедоступным (paywall), поэтому я не могу связать его здесь, но в Интернете доступно множество материалов курса по CS, в которых описаны алгоритм, я также использовал их, например:

http://www.cs.ucsb.edu/~suri/cs235/Triangulation.pdf https://www.cs.umd.edu/class/spring2012/cmsc754/Lects/cmsc754-lects.pdf (см. "Лекцию 6". 'глава)

Я прочитал довольно много из них. Почти каждый набор слайдов, бумаги, блога или любого другого описания алгоритма специально упоминает вершины с равными x-координатами (или y-координатами, если использовать горизонтальную линию развертки), но все они просто говорят: "Мы предполагаем, что нет равных x- координаты "и что это ограничение" легко фиксируется и служит только для упрощения представления "или" не является фундаментальным для алгоритма "или чего-либо еще. Странно, что ни одному из них не нужно подробно останавливаться на требуемых изменениях или обходных путях для поддержки этого случая, или они содержат какое-то нечеткое утверждение о сортировке равных x-вершин таким образом, который на практике не решает проблему.

Может быть, я просто немного глуп или пропускаю что-то действительно очевидное, но я уже несколько дней бездельничаю, пытаясь исправить этот угловой случай безрезультатно, и это начинает становиться действительно разочаровывающим. Я предполагал реализовать алгоритм для основного случая (который включает в себя написание структуры данных DCEL, алгоритма линии развертки, отсортированной карты границ, тригонометрии, необходимой для определения внутренних углов и видимости, структур данных для эффективного хранения и поиска классификаций вершин и т. Д.) - это почти вся работа, и впоследствии исправление проблемы с вертикальными краями будет тривиальным. Прямо сейчас я потратил больше времени, пытаясь исправить вертикальные ребра, чем на все остальные вещи, которые мне понадобились, чтобы объединить алгоритм для общего случая (он отлично работает для любого многоугольника, который я на него набрасываю, если только он этого не делает). имеют вертикальные края).

Спасибо! Wouter

Answer 1

Я наконец-то понял это сам, поэтому я отвечу на свой вопрос для потомков;-)

Оказывается, что изменения в алгоритме триангуляции для полигонов с вертикальными ребрами минимальны, и для их обработки не требуется особых случаев. Мне пришлось изменить следующие вещи:

1. Сортировать вершины с равными x-координатами по возрастающей y-координате (примечание: я использую вертикальную линию развертки, для сортировки по горизонтальной линии развертки сначала y, затем x)
2. Классифицируйте вершины с падающими вертикальными ребрами как "слияние" или "разделение" вместо "обычного вверх / вниз" (он же "верхняя цепь / нижняя цепь")
3. Никогда не добавляйте диагонали, если последние 2 точки цепи рефлекса и текущая вершина линии развертки коллинеарны

Первое требование упоминается в большинстве работ по алгоритму. Сортировка снизу вверх имеет тот же эффект символического вращения по часовой стрелке, как упоминал Дэвид Эйзенстат.

Второе изменение, которое я должен был сделать, было потому, что я неправильно истолковал различные классификации вершин. Мое предположение состояло в том, что у вершины слияния всегда должны быть оба инцидентных ребра полностью слева от нее, а у расщепленной вершины - полностью справа, что неверно. Если один из 2 инцидентных ребер является вертикальным, а другой слева от вершины, он должен быть классифицирован как "объединение", если другой ребро направо, он должен быть классифицирован как "разделение". В частности, мне пришлось изменить следующие строки из этого:

// Classify vertex based on the interior angle and which side of the sweep line the two edges are
BOOL reflex_vertex = (interiorAngle < 0);

BOOL both_left = (e_in.origin.coordinates.x < vertex.coordinates.x) && (e_out.destination.coordinates.x < vertex.coordinates.x);
BOOL both_right = (e_in.origin.coordinates.x > vertex.coordinates.x) && (e_out.destination.coordinates.x > vertex.coordinates.x);

if (!reflex_vertex && both_right)
  type = K14SweepLineVertexTypeStart;

else if (!reflex_vertex && both_left)
  type = K14SweepLineVertexTypeEnd;

else if (reflex_vertex && both_right)
  type = K14SweepLineVertexTypeSplit;

else if (reflex_vertex && both_left)
  type = K14SweepLineVertexTypeMerge;

else if ([_lowerChainVertices containsObject:@(vertex.id)])
  type = K14SweepLineVertexTypeLowerChain;

else
  type = K14SweepLineVertexTypeUpperChain;

К этому:

// Classify vertex based on the interior angle and which side of the sweep line the two edges are
BOOL reflex_vertex = (interiorAngle < 0);

BOOL both_left = (e_in.origin.coordinates.x <= vertex.coordinates.x) && (e_out.destination.coordinates.x <= vertex.coordinates.x);
BOOL both_right = (e_in.origin.coordinates.x >= vertex.coordinates.x) && (e_out.destination.coordinates.x >= vertex.coordinates.x);

...

Последнее изменение было необходимо для предотвращения вырожденных треугольников с 3 коллинеарными точками на выходе. При триангуляции монотонных подкомпонентов всякий раз, когда вершина находится в той же многоугольной цепочке, что и вершины стека ("цепочка рефлекса"), диагонали добавляются из текущей вершины линии развертки ко всем видимым вершинам цепочки рефлекса. В моей реализации видимость определялась путем просмотра (подписанного) внутреннего угла вершины в верхней части стека. Эта проверка смотрела только на знак угла, где положительный угол означает видимый (внутренняя часть меньше или равна пи радиан, или 180 градусов). Проблема была с или равной частью, если 2 точки на вершине стека плюс текущая вершина линии развертки коллинеарны, внутренний угол равен точно пи радианам, и диагональ не должна быть добавлена. Я должен был изменить чек с этого:

BOOL visible = (vi_x_interior_angle > 0.0f);

К этому:

BOOL visible = (vi_x_interior_angle > 0.0f) && ((vi_x_interior_angle + COMPARE_EPSILON) < M_PI);

Я использую небольшой эпсилон, который на самом деле не нужен, если ваши вершины статичны / жестко закодированы, а x-координаты вертикальных ребер точно совпадают, но в моем случае вершины могут быть вычислены и могут иметь небольшую ошибку округления. Не добавление диагонали в случае, когда 3 точки почти точно коллинеарны, в целом должно давать лучшие результаты, чем добавление треугольника с практически нулевой площадью.

Помимо этих трех вещей, никакой специальной обработки не требуется, чтобы алгоритм работал для любого простого многоугольника (без самопересечения, без дырок), который вы бросаете в него. Я немного обескуражен тем, что потратил как минимум 20 часов, чтобы понять это, но, по крайней мере, я наконец-то заработал эту глупость. Просто хотелось бы, чтобы хотя бы одна из многих статей, которые я читал об этом конкретном алгоритме, была бы немного более ясной о трех вещах, которые я пропустил в своей реализации:-/

Answer 2

В нашем двигателе стреловидности мы используем полное лексикографическое упорядочение среди всех точек, где мы рассматриваем y координировать, чтобы быть главной координатой и x координируйте мне второстепенную координату (в нашем случае мы перемещаемся в направлении снизу вверх). В нашей реализации, чтобы обобщить обработку точек, имеющих одинаковые y координаты, мы предполагаем, что точки, которые расположены позже во входной очереди (имеют большую x координаты) в то же время расположены немного "выше" на плоскости на бесконечно малую величину. Это, очевидно, концептуальный вариант преобразования сдвига с помощью некоторого бесконечно малого количества сдвига, о котором уже упоминалось в комментариях.

И, как вы уже упоминали выше, побочным эффектом этого подхода является то, что в общем случае он приводит к образованию "ненужных" срезов на этапе монотонизации, как показано ниже

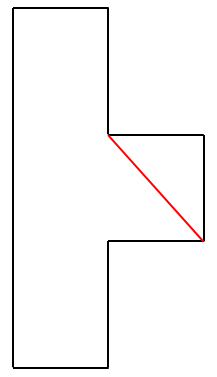
Несмотря на то, что форма уже монотонна вдоль вертикального направления, алгоритм считает необходимым добавить режущую кромку, показанную красным (опять же, в этом случае мы выполняем движение снизу вверх). Но поскольку нашей конечной целью в любом случае является триангуляция, это не большая проблема. Конечно, если у вас есть некоторые дополнительные ограничения на качество конечной триангуляции, то эти "ранние" треугольники могут стать проблемой.

В моем случае триангуляция генерируется, чтобы служить входом для алгоритма, который выполняет кинетическое преобразование начальной триангуляции. Чтобы быть надежными, алгоритмы кинетической триангуляции должны в любом случае иметь дело с "плохими" иглоподобными треугольниками, по этой причине я не налагаю никаких ограничений на качество триангуляции.