Использование python и networkx для нахождения функции плотности вероятности
Я изо всех сил пытаюсь нарисовать график степенного закона для данных Facebook, которые я нашел в Интернете. Я использую Networkx, и я нашел, как нарисовать гистограмму степени и звание степени. Проблема, с которой я столкнулся, заключается в том, что я хочу, чтобы ось y была вероятностью, поэтому я предполагаю, что мне нужно суммировать каждое значение y и делить на общее количество узлов? Может кто-нибудь, пожалуйста, помогите мне сделать это? Как только я получу это, я хотел бы нарисовать график log-log, чтобы посмотреть, смогу ли я получить прямую линию. Буду очень признателен, если кто-нибудь сможет помочь! Вот мой код:
import collections
import networkx as nx
import matplotlib.pyplot as plt
from networkx.algorithms import community
import math
import pylab as plt
g = nx.read_edgelist("/Users/Michael/Desktop/anaconda3/facebook_combined.txt","r")
nx.info(g)
degree_sequence = sorted([d for n, d in g.degree()], reverse=True)
degreeCount = collections.Counter(degree_sequence)
deg, cnt = zip(*degreeCount.items())
fig, ax = plt.subplots()
plt.bar(deg, cnt, width=0.80, color='b')
plt.title("Degree Histogram for Facebook Data")
plt.ylabel("Count")
plt.xlabel("Degree")
ax.set_xticks([d + 0.4 for d in deg])
ax.set_xticklabels(deg)
plt.show()
plt.loglog(degree_sequence, 'b-', marker='o')
plt.title("Degree rank plot")
plt.ylabel("Degree")
plt.xlabel("Rank")
plt.show()
1 ответ
Кажется, вы на правильном пути, но некоторые упрощения, вероятно, помогут вам. Код ниже использует только 2 библиотеки.
Без доступа к вашему графику мы можем использовать некоторые генераторы графиков. Я выбрал 2 качественно разных типа и намеренно выбрал разные размеры, чтобы была необходима нормализация гистограммы.
import networkx as nx
import matplotlib.pyplot as plt
g1 = nx.scale_free_graph(1000, )
g2 = nx.watts_strogatz_graph(2000, 6, p=0.8)
# we don't need to sort the values since the histogram will handle it for us
deg_g1 = nx.degree(g1).values()
deg_g2 = nx.degree(g2).values()
# there are smarter ways to choose bin locations, but since
# degrees must be discrete, we can be lazy...
max_degree = max(deg_g1 + deg_g2)
# plot different styles to see both
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(deg_g1, bins=xrange(0, max_degree), density=True, histtype='bar', rwidth=0.8)
ax.hist(deg_g2, bins=xrange(0, max_degree), density=True, histtype='step', lw=3)
# setup the axes to be log/log scaled
ax.set_yscale('log')
ax.set_xscale('log')
ax.set_xlabel('degree')
ax.set_ylabel('relative density')
ax.legend()
plt.show()
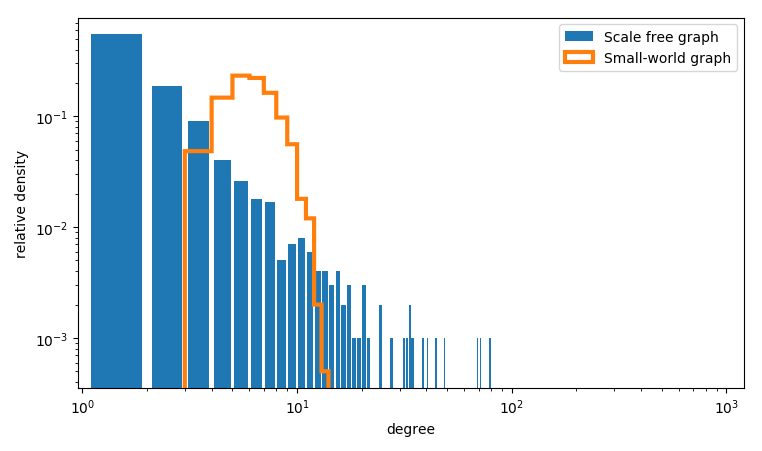
Это создает выходной график, подобный этому (оба g1,g2 рандомизированы, поэтому не будут идентичны):
Здесь мы можем видеть, что g1 имеет приблизительно прямолинейное затухание в распределении степеней - как и ожидалось для безмасштабных распределений по осям log-log. Наоборот, g2 не имеет безмасштабного распределения степеней.
Чтобы сказать что-то более формальное, вы можете взглянуть на наборы инструментов от Аарона Клаусета: http://tuvalu.santafe.edu/~aaronc/powerlaws/ которые реализуют подбор моделей и статистическое тестирование степенных распределений.