Использование основной теоремы для расчета асимптотической временной сложности алгоритма

Question

Проблема: у вас есть алгоритм, который делит проблему размера n на шесть подзадач размером с четверть оригинала. Для деления алгоритм составляет 100 шагов, а для слияния 75н. Сколько времени асимптотическая сложность алгоритма?

Итак, формула для основной теоремы

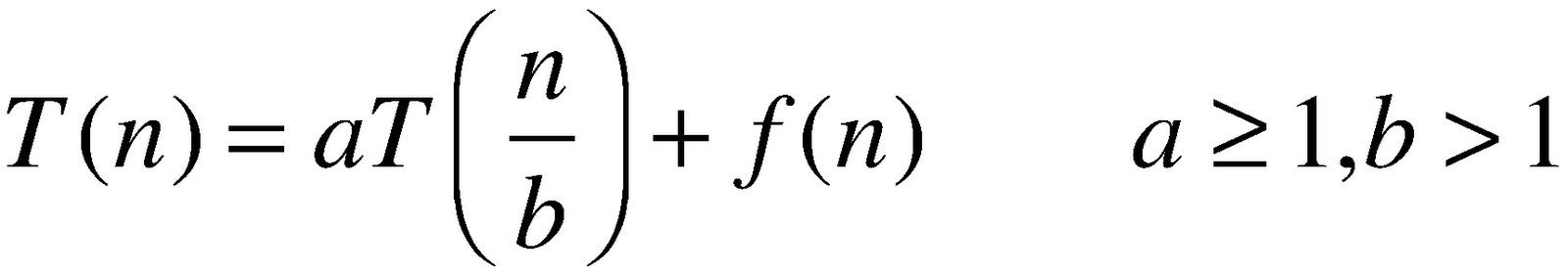
и для этой проблемы a = 6 и b = 4, но я не знаю, где разместить информацию о делении и слиянии.

Приемлемые результаты:O(n^1,2924), омега(n^1,2) и O(1,001ⁿ)

Answer 1

Каждый раз, когда вы решаете подзадачу, вы должны разделить текущий экземпляр на несколько подзадач (стоимость = 100 шаги). Затем необходимо объединить результаты подзадач (стоимость = 75n шаги).

Это означает f(n) = 75n + 100 так как f(n) представляет собой стоимость решения одной подзадачи (исключая стоимость рекурсии).

f(n) = 75n + 100 является O(n),

Поэтому вы смотрите на: T(n) = 6 * T(n/4) + O(n)

И мы знаем, что:

a = 6
b = 4
f(n) = 75n + 100

Далее рассчитаем log_b(a) = log_4(6) = log(6)/log(4) = 1.2924...

Давайте рассмотрим первый случай основной теоремы:

Если f(n) = O(n^c) где c < log_b(a), затем T(n) = Ө(n^(log_b(a)),

Мы знаем это f(n) = O(n^1), так давайте попробуем c = 1,

Является c < log_b(a)? Что ж, 1 < 1.2924..., так да.

Таким образом, T(n) = Ө(n^(log_b(a)) => T(n) = Ө(n^1.2924...),