Триангуляция Делоне - первое преимущество при слиянии

Question

Я пытаюсь реализовать алгоритм "Разделяй и властвуй" для триангуляции Делоне, найденный здесь, но столкнулся с проблемой. При объединении двух наборов я должен найти самый нижний край между ними, который не пересекает ни один из ребер, уже находящихся на графике.

Моя первая проблема в том, что самое нижнее вообще не определено, и это не очевидно. Я читал, например, много текстов, что можно безопасно использовать ребро между вершинами с самыми низкими значениями y в двух наборах, но это не так, как видно на этом изображении: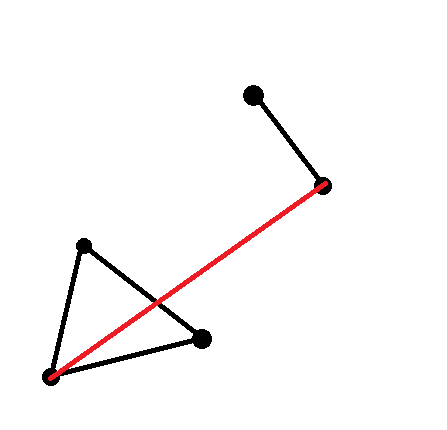

Я почти уверен, что хотя бы один из этих пунктов должен быть частью этого края, но я все равно не могу доказать это.

Я не хочу проверять каждую пару ребер на графиках, потому что для больших наборов данных это может занять слишком много времени.

Поэтому я ищу способ найти этот базовый край. Любая помощь будет оценена.

Answer 1

Я почти уверен, я только что понял это. После получения вершин с наименьшими значениями y я пробежал по обоим наборам и искал две вершины, которые находятся под линией (или на ней), образованной ранее выбранными вершинами, и имеют наибольшее расстояние от нее. Если две точки имеют одинаковое расстояние от линии, я выбрал ту, которая имела наибольшее значение x в случае левого набора и самую низкую в случае правого.

Кажется, это работает очень хорошо. Это потому, что я заметил, что для того, чтобы произошло пересечение, должна быть точка под этой линией, которая является частью ребра, пересекающего наше базовое ребро. Таким образом, я думаю, что я нашел нижнюю границу, касательную к обоим наборам, а это означает, что если я поверну этот набор, так что эта линия будет горизонтальной, то под ней не будет точек.

Answer 2

Я пришел к следующему алгоритму:

1. построить выпуклую оболочку, используя алгоритм монотонной цепи Эндрю.
2. получить ребра выпуклой оболочки, не входящие в субтриангуляции выпуклой оболочки.
3. нижняя из полученных кромок является требуемой базовой кромкой.

Обратите внимание на третий шаг: сегмент S1 считается ниже другого сегмента S2 если ориентация S2 (какие конечные точки берутся в порядке возрастания x координата) с обеими конечными точками S1 не против часовой стрелки, т.е. S1 никогда не бывает слева от S2 если мы идем дальше S2.

Заметки о сложности времени

1. поскольку в начале алгоритма D&C мы лексикографически сортируем точки по x а затем y, построение выпуклой оболочки субтриангуляций будет O(n) (сортировка не требуется), где n - количество точек в обеих субтриангуляциях.
2. мы можем использовать контейнеры с O(1) поиск (например, хеш-таблицы) ребер субтриангуляции и фильтрация в O(n).
3. поиск самого нижнего края можно выполнить в O(n).

поэтому общий процесс потребует O(n) операции.