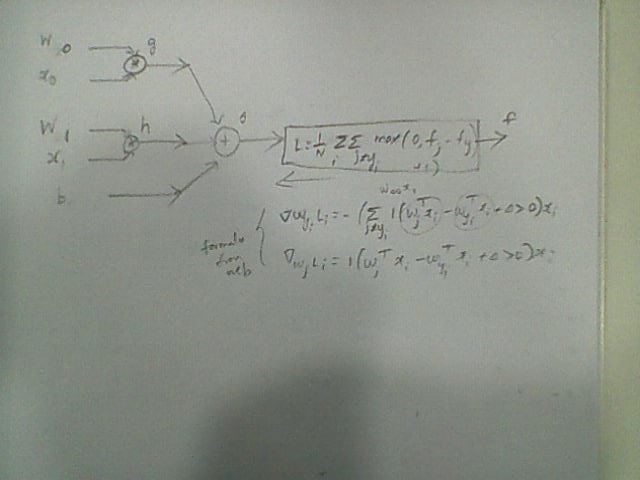
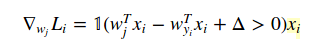Расчет градиента (обратное распространение) для SVM вместе с формулой
Я могу рассчитать оценки прямого распространения. Может ли кто-нибудь предоставить мне расчет обратного распространения для значений, представленных здесь. Также, пожалуйста, объясните, как нарисованы линии на графике и как он изменяется при нажатии "начать повторное обновление параметра". Пожалуйста, предоставьте пример расчета / объяснения значений по умолчанию при загрузке страницы.
http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/
Ниже приведен график для расчета (я не уверен, что он на 100% правильный)
формула для расчета градиентных потерь
1 ответ
Посетите https://stats.stackexchange.com/questions/155088/gradient-for-hinge-loss-multiclass , чтобы получить несколько ответов, объясняющих обратное происхождение потери данных (многоклассовая потеря SVM).
Обратное подтверждение потерь регуляризации (L2) равно2 * lambda * W. Вы добавляете это к dL/dW из-за потери данных.
Примечание: предвзятости не отражаются в регуляризации, потому что мы не хотим наказывать пересечение оси Y наших изученных границ принятия решений. Наказание за пересечение оси y будет означать, что смещение будет близко к нулю, поэтому каждая граница решения будет проходить близко к началу координат.
«Начать повторное обновление параметров» по сути включает градиентный спуск для обновления весов линейного классификатора, заданных:
- Функция потерь (выбор в правом нижнем углу)
- Сила регуляризации L2 (ползунок в правом нижнем углу)
- Размер шага (ползунок над кнопками)
Цветные линии — это границы решений для каждого из трех классов. Стрелка указывает в сторону положительного результата (W dot x + b). Каждая строка весов и смещений относится к одному классу. Эти два элемента контролируют наклон границ решения, а смещение управляет пересечением оси y.
Градиентный спуск автоматически изучает и минимизирует общие потери (потеря данных + потеря регуляризации). Поскольку обучение продолжается,Wиbобновляются, и поэтому мы видим, как границы решений перемещаются.
В конце концов, обучение выходит на плато, когда решатель «сходится» (приближается к минимально возможным потерям), и границы решения перестают смещаться.