Проверка нормальности дистрибутива в python

Question

У меня есть некоторые данные, которые я выбрал из радиолокационного спутникового изображения и хотел выполнить некоторые статистические тесты. Перед этим я хотел провести тест на нормальность, чтобы быть уверенным, что мои данные были нормально распределены. Мои данные, кажется, нормально распределены, но когда я выполняю тест, я получаю Pvalue 0, предполагая, что мои данные обычно не распространяются.

Я приложил свой код вместе с выводом и гистограммой распределения (я относительно новичок в python, поэтому извиняюсь, если мой код каким-то неуклюжим). Может кто-нибудь сказать мне, если я делаю что-то не так - мне трудно поверить из моей гистограммы, что мои данные обычно не распространяются?

values = 'inputfile.h5'
f = h5py.File(values,'r')
dset = f['/DATA/DATA']
array = dset[...,0]
print('normality =', scipy.stats.normaltest(array))
max = np.amax(array)
min = np.amin(array)

histo = np.histogram(array, bins=100, range=(min, max))
freqs = histo[0]
rangebins = (max - min)
numberbins = (len(histo[1])-1)
interval = (rangebins/numberbins)
newbins = np.arange((min), (max), interval)
histogram = bar(newbins, freqs, width=0.2, color='gray')
plt.show()

Это печатает это: (41099.095955202931, 0.0). первый элемент является значением хи-квадрат, а второй - значением.

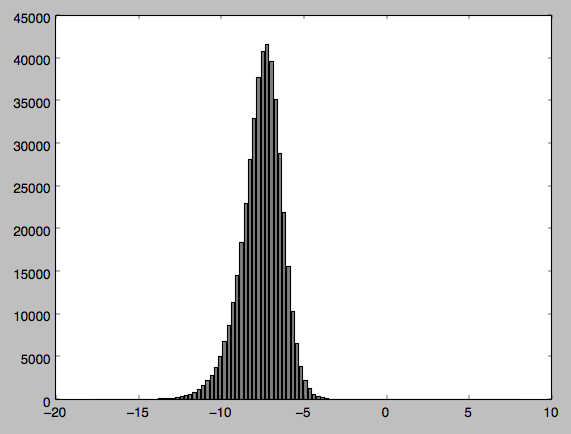
Я сделал график данных, которые я приложил. Я подумал, что, возможно, поскольку я имею дело с отрицательными значениями, это вызывает проблему, поэтому я нормализовал значения, но проблема сохраняется.

Answer 1

В общем случае, когда количество образцов меньше 50, следует соблюдать осторожность при использовании тестов на нормальность. Поскольку эти тесты нуждаются в достаточном количестве доказательств, чтобы отвергнуть нулевую гипотезу, а именно: "распределение данных является нормальным", а когда количество выборок невелико, они не могут найти эти доказательства.

Имейте в виду, что когда вы не можете отвергнуть нулевую гипотезу, это не означает, что альтернативная гипотеза верна.

Существует еще одна возможность: Некоторые реализации статистических тестов на нормальность сравнивают распределение ваших данных со стандартным нормальным распределением. Чтобы избежать этого, я предлагаю вам стандартизировать данные и затем применить тест нормальности.

Answer 2

Этот вопрос объясняет, почему вы получаете такое маленькое значение p. По сути, тесты нормальности почти всегда отклоняют нулевое значение при очень больших размерах выборки (например, в вашем случае вы можете видеть только некоторую перекос в левой части, что при вашем огромном размере выборки более чем достаточно).

Что было бы гораздо более практичным в вашем случае, так это построить нормальную кривую, соответствующую вашим данным. Затем вы можете увидеть, как на самом деле отличается нормальная кривая (например, вы можете увидеть, действительно ли хвост на левой стороне слишком длинный). Например:

from matplotlib import pyplot as plt
import matplotlib.mlab as mlab

n, bins, patches = plt.hist(array, 50, normed=1)
mu = np.mean(array)
sigma = np.std(array)
plt.plot(bins, mlab.normpdf(bins, mu, sigma))

(Обратите внимание normed=1 аргумент: это гарантирует, что гистограмма нормализуется, чтобы иметь общую площадь 1, что делает ее сопоставимой с плотностью, такой как нормальное распределение).