Решить PNP против восстановления Позировать по ротационной композиции: почему переводы не одинаковы?

Question

---

Часть 1: до обновления

---

Я пытаюсь оценить относительное положение, используя два разных метода: solvePNP и recoverPose, и кажется, что матрицы R выглядят нормально с некоторой ошибкой, но векторы трансляции совершенно разные. Что я делаю неправильно? В общем, мне нужно найти относительное положение от кадра 1 до кадра 2, используя оба метода.

    cv::solvePnP(constants::calibration::rig.rig3DPoints, corners1,
                 cameraMatrix, distortion, rvecPNP1, tvecPNP1);
    cv::solvePnP(constants::calibration::rig.rig3DPoints, corners2,
                 cameraMatrix, distortion, rvecPNP2, tvecPNP2);

    Mat rodriguesRPNP1, rodriguesRPNP2;
    cv::Rodrigues(rvecPNP1, rodriguesRPNP1);
    cv::Rodrigues(rvecPNP2, rodriguesRPNP2);

    rvecPNP = rodriguesRPNP1.inv() * rodriguesRPNP2;
    tvecPNP = rodriguesRPNP1.inv() * (tvecPNP2 - tvecPNP1);

    Mat E = findEssentialMat(corners1, corners2, cameraMatrix);

    recoverPose(E, corners1, corners2, cameraMatrix, rvecRecover, tvecRecover);

Выход:

solvePnP: R: 
[0.99998963, 0.0020884471, 0.0040569459;
-0.0020977913, 0.99999511, 0.0023003994;
-0.0040521105, -0.0023088832, 0.99998915]

solvePnP: t:  
[0.0014444492; 0.00018377086; -0.00045027508]

recoverPose: R: 
[0.9999900052294586, 0.0001464890570028249, 0.004468554816042664;
-0.0001480011106435358, 0.9999999319097322, 0.0003380476328946509;
-0.004468504991498534, -0.0003387056052618761, 0.9999899588204144]

recoverPose: t: 
[0.1492094050828522; -0.007288328116585327; -0.9887787587261805]

---

Часть 2: после обновления

---

Обновление: я изменил способ, которым R- ы и t- ы составлены после solvePnP:

    cv::solvePnP(constants::calibration::rig.rig3DPoints, corners1,
                 cameraMatrix, distortion, rvecPNP1, tvecPNP1);
    cv::solvePnP(constants::calibration::rig.rig3DPoints, corners2,
                 cameraMatrix, distortion, rvecPNP2, tvecPNP2);

    Mat rodriguesRPNP1, rodriguesRPNP2;
    cv::Rodrigues(rvecPNP1, rodriguesRPNP1);
    cv::Rodrigues(rvecPNP2, rodriguesRPNP2);

    rvecPNP = rodriguesRPNP1.inv() * rodriguesRPNP2;
    tvecPNP = rodriguesRPNP2 * tvecPNP2 - rodriguesRPNP1 * tvecPNP1;

Эта композиция была проверена с фактическими движениями камеры и кажется правильным.

Кроме того, recoveryPose теперь получает очки от неплоского объекта, и эти точки находятся в общем положении. Проверенное движение также не было чистым вращением, чтобы избежать вырожденного случая, но векторы переноса сильно отличаются.

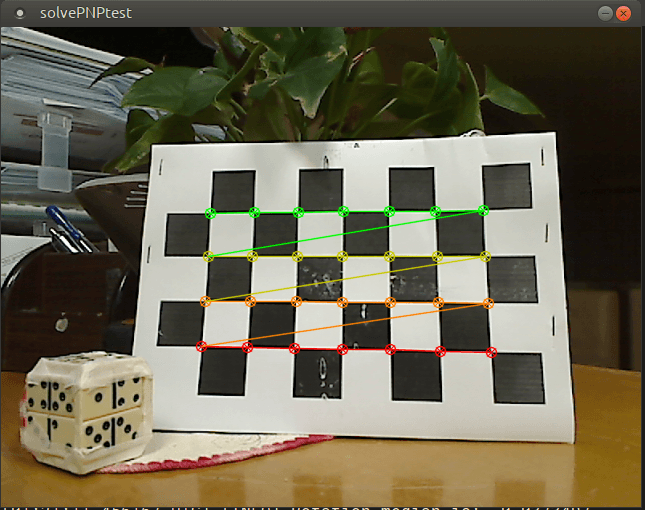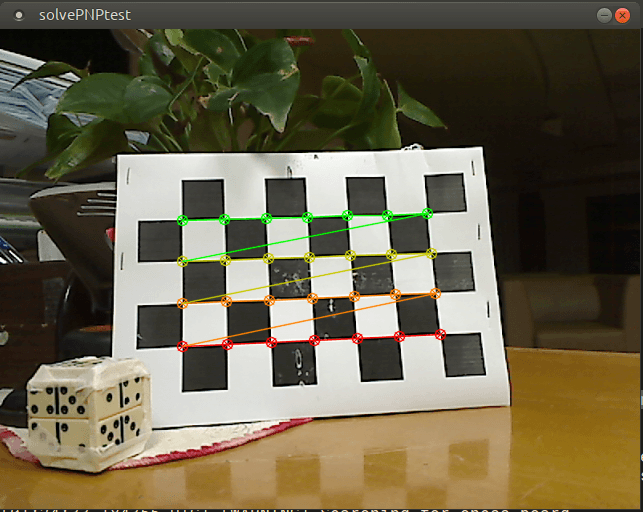Первый кадр: Первый кадр: зеленые точки отслеживаются и сопоставляются, и их можно увидеть на втором кадре (хотя на втором кадре они синего цвета): Второй кадр: Второй кадр: отслеживаемые точки в общем положении для восстановления.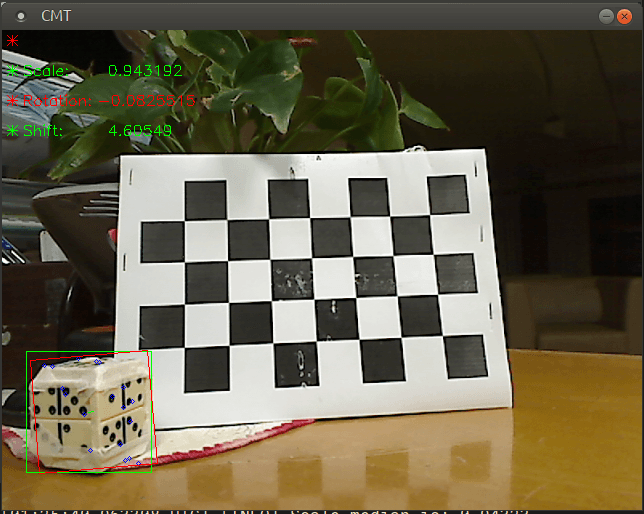

    cv::solvePnP(constants::calibration::rig.rig3DPoints, corners1,
                 cameraMatrix, distortion, rvecPNP1, tvecPNP1);
    cv::solvePnP(constants::calibration::rig.rig3DPoints, corners2,
                 cameraMatrix, distortion, rvecPNP2, tvecPNP2);

    Mat rodriguesRPNP1, rodriguesRPNP2;
    cv::Rodrigues(rvecPNP1, rodriguesRPNP1);
    cv::Rodrigues(rvecPNP2, rodriguesRPNP2);

    rvecPNP = rodriguesRPNP1.inv() * rodriguesRPNP2;
    tvecPNP = rodriguesRPNP2 * tvecPNP2 - rodriguesRPNP1 * tvecPNP1;

    CMT cmt;
    // ...
    // ... cmt module finds and tracks points here
    // ...
    std::vector<Point2f> coords1 = cmt.getPoints();
    std::vector<int> classes1 = cmt.getClasses();

    cmt.processFrame(imGray2);

    std::vector<Point2f> coords2 = cmt.getPoints();
    std::vector<int> classes2 = cmt.getClasses();

    std::vector<Point2f> coords3, coords4;

    // Make sure that points and their classes are in the same order 
    // and the vectors of the same size
    utils::fuse(coords1, classes1, coords2, classes2, coords3, coords4,
                constants::marker::randomPointsInMark);

    Mat E = findEssentialMat(coords3, coords4, cameraMatrix, cv::RANSAC, 0.9999);

    int numOfInliers = recoverPose(E, coords3, coords4, cameraMatrix,
                                   rvecRecover, tvecRecover);

Выход:

solvePnP: R:
[ 0.97944641,  0.072178222,  0.18834825;
 -0.07216832,  0.99736851,  -0.0069195116;
 -0.18835205, -0.0068155089, 0.98207784]

solvePnP: t:
[-0.041602995; 0.014756925; 0.025671512]

recoverPose: R:
[0.8115000456601129,  0.03013366385237642, -0.5835748779689431;
 0.05045522914264587, 0.9913266281414459,   0.1213498503908197;
 0.5821700316452212, -0.1279198133228133,   0.80294120308629]

recoverPose: t:
[0.6927871089455181; -0.1254653960405977; 0.7101439685551703]

recoverPose: numOfInliers: 18

Я также пробовал случай, когда камера стоит на месте (нет R, нет T), и R- ы близки, но переводы нет. Так чего мне здесь не хватает?

Answer 1

Если вы используете систему монокулярных камер для определения относительного положения между кадрами, то, разложив основную матрицу, вы не сможете получить абсолютный перевод в реальном мире. Обратите внимание, что все векторы трансляции, которые вы получаете от recoverPose(), являются единичными векторами. "Разлагая E, вы можете получить только направление перевода, поэтому функция возвращает единицу измерения t.", Из документа degposeEssentialMat ().

А для solvePnP() он использует трехмерные точки мировой системы координат. Таким образом, перевод, рассчитанный по алгоритму solvePnP(), должен быть абсолютным значением в реальном мире. Для вращения R оба метода дают правильный ответ.