Получите стандартизированные остатки и график "Остаток против приспособленного" для объекта "mlm" из `lm()`
set.seed(0)
## 2 response of 10 observations each
response <- matrix(rnorm(20), 10, 2)
## 3 covariates with 10 observations each
predictors <- matrix(rnorm(30), 10, 3)
fit <- lm(response ~ predictors)
Я генерировал остаточные графики для всей модели, используя:
plot(fitted(fit),residuals(fit))
Тем не менее, я хотел бы сделать отдельные графики для каждого ковариата предиктора. Я могу сделать их по одному:
f <- fitted(fit)
r <- residual(fit)
plot(f[,1],r[,1])
Однако проблема этого подхода заключается в том, что он должен быть обобщаемым для наборов данных с большим количеством ковариат предикторов. Есть ли способ, которым я использую plot, итерируя по каждому столбцу (f) и (r)? Или есть способ, которым plot() Можно ли сгруппировать каждый из них по цвету?
2 ответа
Убедитесь, что вы используете стандартизированные остатки, а не сырые остатки
Я часто вижу plot(fitted(fit), residuals(fit)) но это статистически неправильно. Мы используем plot(fit) создать диагностический график, потому что нам нужны стандартизированные остатки, а не сырые. Читать ?plot.lm для большего. Но plot Метод для "млм" плохо поддерживается:
plot(fit)
# Error: 'plot.mlm' is not implemented yet
Определить "стандарт" метод S3 для "млм"
plot.mlm не поддерживается по многим причинам, одной из которых является отсутствие rstandard.mlm, Для классов "lm" и "glm" существует универсальный метод S3 "rstandard" для получения стандартизированных остатков:
methods(rstandard)
# [1] rstandard.glm* rstandard.lm*
Нет поддержки для "MLM". Таким образом, мы должны заполнить этот пробел в первую очередь.
Нетрудно получить стандартизированные остатки. Позволять hii быть диагоналями шляпной матрицы, точечная оценочная стандартная ошибка для остатков равна sqrt(1 - hii) * sigma, где sigma = sqrt(RSS / df.residual) оценивается остаточная стандартная ошибка. RSS остаточная сумма квадратов; df.residual это остаточная степень свободы.
hii может быть вычислено из матричного фактора Q QR факторизации модельной матрицы: rowSums(Q ^ 2), Для "mlm" существует только одно разложение QR, поскольку матрица модели одинакова для всех ответов, поэтому нам нужно только вычислить hii один раз.
Разный ответ имеет разный sigma, но они элегантно colSums(residuals(fit) ^ 2) / df.residual(fit),
Теперь давайте подведем итог этим идеям, чтобы получить наш собственный "rstandard" метод для "mlm":
## define our own "rstandard" method for "mlm" class
rstandard.mlm <- function (model) {
Q <- with(model, qr.qy(qr, diag(1, nrow = nrow(qr$qr), ncol = qr$rank))) ## Q matrix
hii <- rowSums(Q ^ 2) ## diagonal of hat matrix QQ'
RSS <- colSums(model$residuals ^ 2) ## residual sums of squares (for each model)
sigma <- sqrt(RSS / model$df.residual) ## ## Pearson estimate of residuals (for each model)
pointwise_sd <- outer(sqrt(1 - hii), sigma) ## point-wise residual standard error (for each model)
model$residuals / pointwise_sd ## standardised residuals
}
Обратите внимание на использование .mlm в имени функции, чтобы сказать R, это связанный с S3 метод. Как только мы определили эту функцию, мы можем увидеть ее в методе "rstandard":
## now there are method for "mlm"
methods(rstandard)
# [1] rstandard.glm* rstandard.lm* rstandard.mlm
Чтобы вызвать эту функцию, нам не нужно явно вызывать rstandard.mlm; призвание rstandard достаточно:
## test with your fitted model `fit`
rstandard(fit)
# [,1] [,2]
#1 1.56221865 2.6593505
#2 -0.98791320 -1.9344546
#3 0.06042529 -0.4858276
#4 0.18713629 2.9814135
#5 0.11277397 1.4336484
#6 -0.74289985 -2.4452868
#7 0.03690363 0.7015916
#8 -1.58940448 -1.2850961
#9 0.38504435 1.3907223
#10 1.34618139 -1.5900891
Стандартизированные остатки N(0, 1) распределены.
Получение остатков против построенного участка для "млм"
Ваша первая попытка с:
f <- fitted(fit); r <- rstandard(fit); plot(f, r)
неплохая идея, при условии, что точки для разных моделей могут быть идентифицированы друг от друга. Поэтому мы можем попробовать использовать разные цвета точек для разных моделей:
plot(f, r, col = as.numeric(col(f)), pch = 19)
Графические аргументы, такие как col, pch а также cex может взять векторный ввод. я спрашиваю plot использовать col = j для r[,j] ~ f[,j], где j = 1, 2,..., ncol(f), Читайте "Спецификация цвета" из ?par для чего col = j средства. pch = 19 говорит plot рисовать сплошные точки. Прочитайте основные графические параметры для различных вариантов.
Наконец, вы можете захотеть легенду. Ты можешь сделать
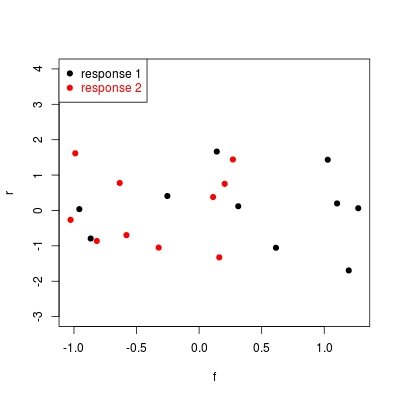
plot(f, r, col = as.numeric(col(f)), pch = 19, ylim = c(-3, 4))
legend("topleft", legend = paste0("response ", 1:ncol(f)), pch = 19,
col = 1:ncol(f), text.col = 1:ncol(f))
Чтобы оставить место для поля легенды, мы расширяем ylim совсем немного. Как стандартизированные остатки N(0,1), ylim = c(-3, 3) хороший выбор Если мы хотим разместить поле легенды в левом верхнем углу, мы расширяем ylim в c(-3, 4), Вы можете настроить свою легенду еще больше через ncol, title, так далее.
Сколько ответов у вас есть?
Если у вас есть не более нескольких ответов, приведенное выше предложение работает хорошо. Если у вас есть много, предлагается построить их на отдельном участке. for Цикл, как вы выяснили, является приличным, за исключением того, что вам нужно разделить область построения на разные вспомогательные участки, возможно, используя par(mfrow = c(?, ?)), Также установите внутреннее поле mar и внешний край oma если вы берете этот подход. Вы можете прочитать Как создать более хороший график для моих категориальных данных временных рядов в матрице? за один пример этого.
Если у вас есть еще больше ответов, вы могли бы хотеть смесь обоих? Скажем, если у вас есть 42 ответа, вы можете сделать par(mfrow = c(2, 3))Затем подготовьте 7 ответов в каждой подфигуре. Теперь решение больше основано на мнении.
Вот как я это решил.
for(i in 1:ncol(f)) {
plot(f[,i],r[,i])
}
Разум взорван.