Создание пересекающихся изображений в matplotlib с помощью imshow или другой функции
У меня есть два трехмерных массива радиолокационных данных. Каждый массив в основном представляет собой коллекцию покадровых 2-D изображений, где время увеличивается по третьему измерению. Я хочу создать трехмерный график, который пересекает двухмерное изображение из каждого массива.
По сути, я пытаюсь создать забор. Некоторые примеры такого типа сюжета можно найти на этих сайтах: http://www.geogiga.com/images/products/seismapper_3d_seismic_color.gif http://www.usna.edu/Users/oceano/pguth/website/so461web/seismic_refl/fence.png
Обычно я использую imshow для индивидуального отображения двухмерных изображений для анализа. Тем не менее, мое исследование функциональности imshow показывает, что он не работает с 3D-осями. Есть ли способ обойти это? Или есть другая функция построения графиков, которая может копировать функциональность imshow, но может быть объединена с трехмерными осями?
2 ответа
Если вы счастливы рассмотреть возможность использования другой библиотеки графиков (т.е. не matplotlib), то, возможно, стоит рассмотреть mayavi / tvtk (хотя кривая обучения немного крутая). Самое близкое, что я видел, к тому, что вы хотите, это скалярные плоскости разреза в http://wiki.scipy.org/Cookbook/MayaVi/Examples
Основная часть документации находится по адресу: http://docs.enthought.com/mayavi/mayavi/index.html
Возможно, есть лучшие способы, но, по крайней мере, вы всегда можете сделать плоскую сетку и раскрасить ее:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
# create a 21 x 21 vertex mesh
xx, yy = np.meshgrid(np.linspace(0,1,21), np.linspace(0,1,21))
# create some dummy data (20 x 20) for the image
data = np.random.random((20, 20))
# create vertices for a rotated mesh (3D rotation matrix)
X = np.sqrt(1./3) * xx + np.sqrt(1./3) * yy
Y = -np.sqrt(1./3) * xx + np.sqrt(1./3) * yy
Z = np.sqrt(1./3) * xx - np.sqrt(1./3) * yy
# create the figure
fig = plt.figure()
# show the reference image
ax1 = fig.add_subplot(121)
ax1.imshow(data, cmap=plt.cm.BrBG, interpolation='nearest', origin='lower', extent=[0,1,0,1])
# show the 3D rotated projection
ax2 = fig.add_subplot(122, projection='3d')
ax2.plot_surface(X, Y, Z, rstride=1, cstride=1, facecolors=plt.cm.BrBG(data), shade=False)
Это создает:
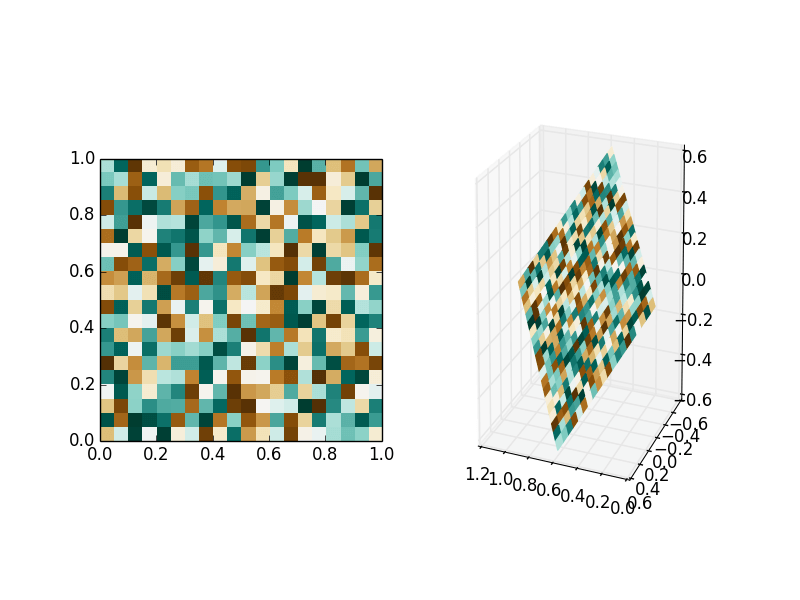
(Обратите внимание, что я не очень внимательно относился к матрице вращения, вам придется создавать собственную проекцию. Возможно, было бы неплохо использовать реальную матрицу вращения.)
Просто отметьте, что есть небольшая проблема с столбами забора и заборами, то есть сетка имеет еще одну вершину по сравнению с количеством заплат.
Подход выше не очень эффективен, если у вас есть изображения с высоким разрешением. Это может даже не быть полезным с ними. Тогда другая возможность заключается в использовании серверной части, которая поддерживает аффинные преобразования изображений. К сожалению, вам придется рассчитывать преобразования самостоятельно. Это не страшно сложно, но все же немного неуклюже, и тогда вы не получите настоящее трехмерное изображение, которое можно вращать вокруг и т. Д.
Для этого подхода см. http://matplotlib.org/examples/api/demo_affine_image.html
В качестве альтернативы, вы можете использовать OpenCV и его cv2.warpAffine функция деформации вашего изображения, прежде чем показывать его с imshow, Если вы заполняете окружение прозрачным цветом, вы можете затем наложить слои изображений, чтобы получить результат, который выглядит как ваш пример iamge.
Просто чтобы дать вам представление о возможностях plot_surfaceЯ попытался деформировать Лену вокруг полуцилиндра:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
# create a 513 x 513 vertex mesh
xx, yy = np.meshgrid(np.linspace(0,1,513), np.linspace(0,1,513))
# create vertices for a rotated mesh (3D rotation matrix)
theta = np.pi*xx
X = np.cos(theta)
Y = np.sin(theta)
Z = yy
# create the figure
fig = plt.figure()
# show the 3D rotated projection
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, facecolors=plt.imread('/tmp/lena.jpg')/255., shade=False)
Она действительно хорошо сгибается, но все операции над изображением довольно медленные:
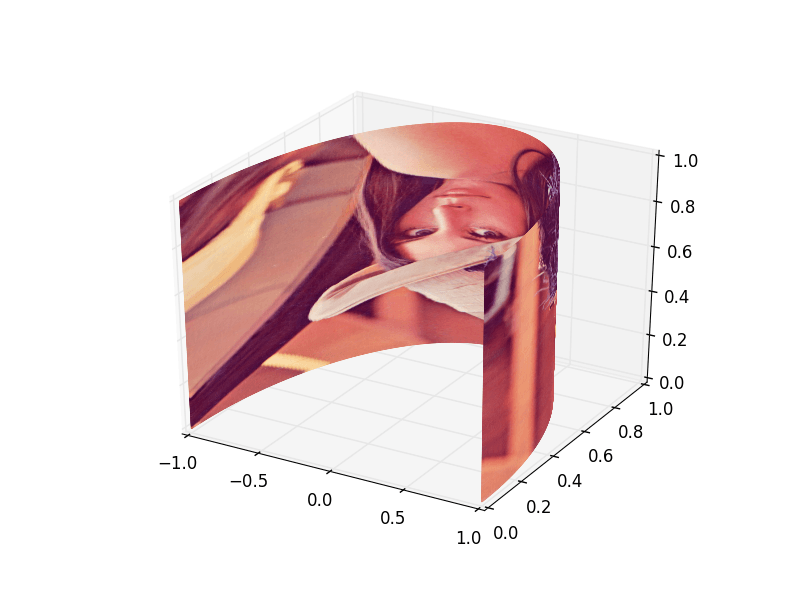
Невозможно сделать это с помощью matplotlib. Ответ @DrV является приблизительным. Matplotlib на самом деле показывает не каждый отдельный пиксель исходного изображения, а некоторое измененное изображение. rstride и cstride позволяют вам указать, как масштабируется изображение, однако вывод не будет точным изображением.