Оценка поезда уменьшается после увеличения степени полиномиальной регрессии

Question

Я пытаюсь использовать линейную регрессию, чтобы подогнать полиномиум к набору точек синусоидального сигнала с добавлением некоторого шума, используя linear_model.LinearRegression от sklearn,

Как и ожидалось, показатели обучения и проверки увеличиваются с увеличением степени полинома, но после некоторой степени около 20 вещей начинают становиться странными, и показатели начинают снижаться, и модель возвращает полиномиумы, которые совсем не похожи на данные, которые Я использую, чтобы тренировать это.

Ниже приведены некоторые графики, на которых это видно, а также код, который сгенерировал как регрессионные модели, так и графики:

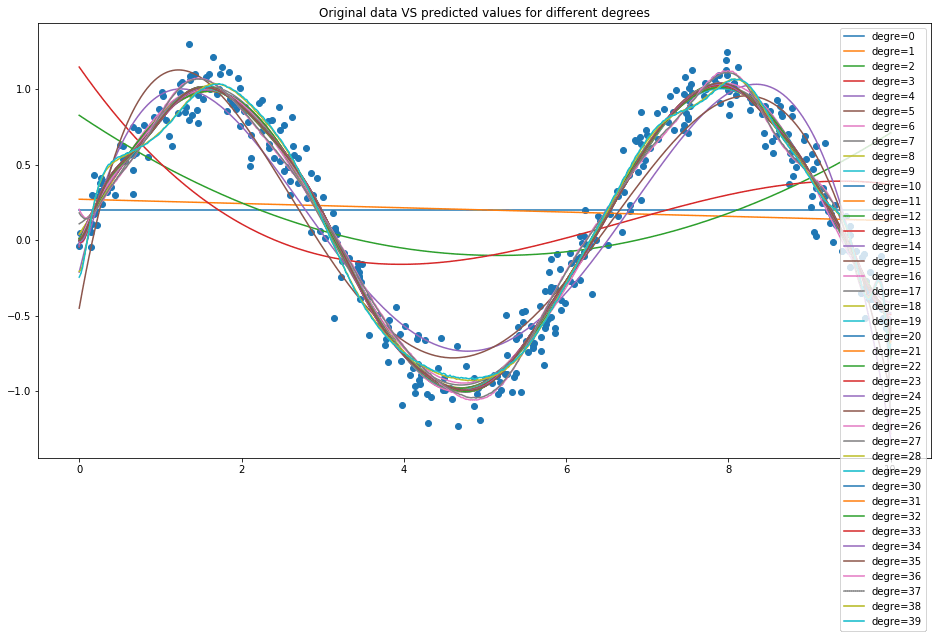
Как вещь работает хорошо до степени =17. Исходные данные против прогнозов:

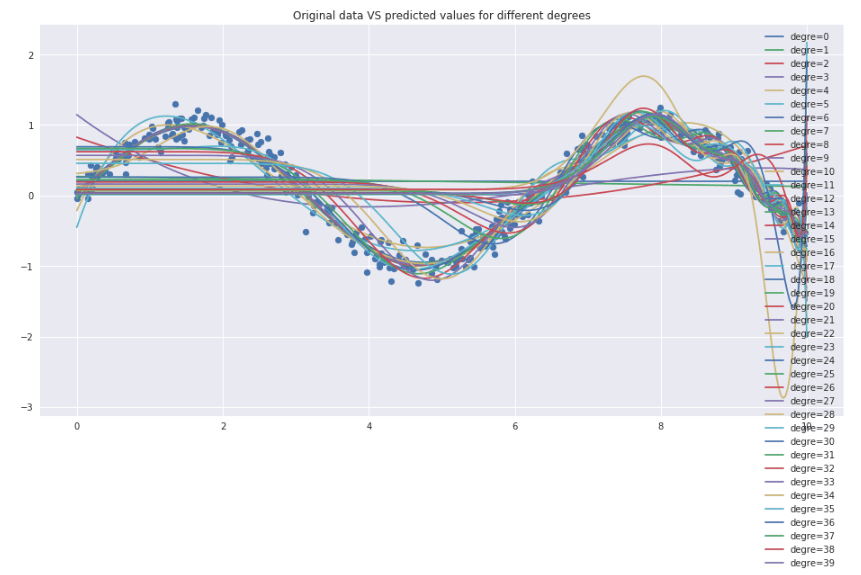
После этого становится только хуже:

Кривая валидации, увеличивающая степень полиномия:

from sklearn.pipeline import make_pipeline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.learning_curve import validation_curve

def make_data(N, err=0.1, rseed=1):
    rng = np.random.RandomState(1)
    x = 10 * rng.rand(N)
    X = x[:, None]
    y = np.sin(x) + 0.1 * rng.randn(N)
    if err > 0:
        y += err * rng.randn(N)
    return X, y

def PolynomialRegression(degree=4):
    return make_pipeline(PolynomialFeatures(degree),
                         LinearRegression())


X, y = make_data(400)

X_test = np.linspace(0, 10, 500)[:, None]
degrees = np.arange(0, 40)

plt.figure(figsize=(16, 8))
plt.scatter(X.flatten(), y)
for degree in degrees:
    y_test = PolynomialRegression(degree).fit(X, y).predict(X_test)
    plt.plot(X_test, y_test, label='degre={0}'.format(degree))
plt.title('Original data VS predicted values for different degrees')
plt.legend(loc='best');


degree = np.arange(0, 40)
train_score, val_score = validation_curve(PolynomialRegression(), X, y,
                                                 'polynomialfeatures__degree',
                                                 degree, cv=7)

plt.figure(figsize=(12, 6))
plt.plot(degree, np.median(train_score, 1), marker='o', 
         color='blue', label='training score')
plt.plot(degree, np.median(val_score, 1), marker='o',
         color='red', label='validation score')
plt.legend(loc='best')
plt.ylim(0, 1)
plt.title('Learning curve, increasing the degree of the polynomium')
plt.xlabel('degree')
plt.ylabel('score');

Я знаю, что ожидаемая вещь состоит в том, что оценка проверки снижается, когда сложность модели увеличивается, но почему снижается и оценка обучения? Чего мне здесь не хватает?

Answer 1

Прежде всего, вот как вы можете это исправить, установив флаг нормализации True для модели;

def PolynomialRegression(degree=4):
    return make_pipeline(PolynomialFeatures(degree),
                         LinearRegression(normalize=True))

Но почему? В линейной регрессииfit() функция находит наиболее подходящую модель с Moore–Penrose inverse который является обычным способом вычисления least-squareрешение. Когда вы добавляете полиномы значений, ваши расширенные функции очень быстро становятся очень большими, если вы не нормализуете. Эти большие значения доминируют в стоимости, вычисляемой методом наименьших квадратов, и приводят к тому, что модель подходит для больших значений, то есть значений полинома более высокого порядка вместо данных.

Сюжеты выглядят лучше и такими, какими они должны быть.

Answer 2

Ожидается, что результат обучения также снизится из-за переобучения модели данными тренировок. Ошибка при валидации уменьшается из-за расширения ряда синусоидальной функции Тейлора. Таким образом, по мере увеличения степени полинома ваша модель улучшается, чтобы лучше соответствовать синусоиде.

В идеальном случае, если у вас нет функции, которая расширяется до бесконечных степеней, вы видите, что ошибка обучения снижается (не монотонно, а в целом), а ошибка проверки увеличивается после некоторой степени (высокая для более низких степеней -> низкая для некоторой более высокой степени) после этого).