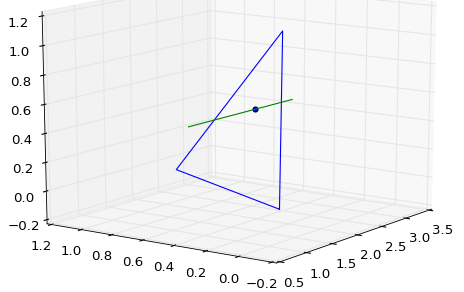
Shapely: точка пересечения между линией и многоугольником в 3D

Question

В прошлый раз, когда я использовал стройные, у меня действительно было это приятное чувство ввоза и полета. Однако в последнее время я столкнулся с довольно неинтуитивным поведением в этом модуле, так как пытался найти пересечение между отрезком и треугольником в трехмерном пространстве. Давайте определим сегмент и треугольник следующим образом:

l = LineString([[1,0.5,0.5],[3,0.5,0.5]])
p = Polygon([[1.2,0.0,0.],[2.2,1.0,0.],[2.8,0.5,1.]])

Чтобы получить их точку пересечения, я использовал l.intersection(p)и ожидал точку, а именно POINT Z (POINT Z (2 0.5 0.25)), Это показано синей точкой ниже:

Вместо этого я получил LINESTRING Z (1.7 0.5 0.25, 2.8 0.5 1) - красная линия внизу - и, честно говоря, я весьма озадачен тем, что он должен представлять.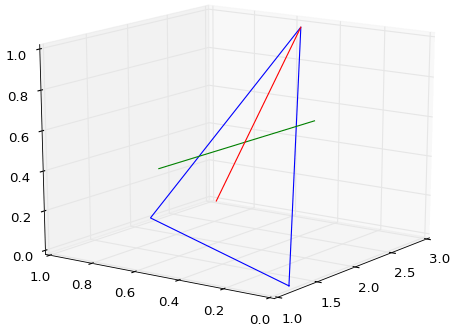

Как ни странно, когда многоугольник / треугольник находится в плоскости xz и ортогонален отрезку линии, функция ведет себя так, как и следовало ожидать. Однако, когда треугольник "наклоняется", он возвращает линию. Это временно привело меня к мысли, что это вернуло пересечение между линией и ограничительной рамкой треугольника. Выше красная линия доказывает обратное.

Поэтому обходной путь для этой проблемы - прочитать эту очень поучительную веб-страницу и адаптировать их. C++ код для работы с стройными объектами. intersection Метод отлично работает, чтобы проверить, проходит ли линия через многоугольник, и функция ниже находит интересующую точку.

def intersect3D_SegmentPlane(Segment, Plane):

    # Points in Segment: Pn  Points in Plane: Qn
    P0, P1     = np.array(Segment.coords)
    Q0, Q1, Q2 = np.array(Plane.exterior)[:-1]   

    # vectors in Plane
    q1 = Q1 - Q0
    q2 = Q2 - Q0

    # vector normal to Plane
    n  = np.cross(q1, q2)/np.linalg.norm(np.cross(q1, q2))
    u = P1 - P0 # Segment's direction vector 
    w = P0 - Q0 # vector from plane ref point to segment ref point

    ## Tests parallelism
    if np.dot(n, u) == 0:
        print "Segment and plane are parallel"
        print "Either Segment is entirely in Plane or they never intersect."
        return None
    ## if intersection is a point
    else:
        ## Si is the scalar where P(Si) = P0 + Si*u lies in Plane
        Si = np.dot(-n, w) / np.dot(n, u)
        PSi = P0 + Si * u
        return PSi

Больше не очень импортно-летать...

Итак, наконец, на мои вопросы:

• Что значит intersection возврат при применении к 3D-объектам и почему это линия?

• Есть ли функция в форме, которая делает то, что я хочу? или любой необязательный аргумент, твик или трюк темной магии?

• Есть ли какие-нибудь другие библиотеки, которые бы выполняли эту работу, осуществляя мои мечты о простоте и лени?

Answer 1

К сожалению, как говорится в документации:

Последовательности координат неизменны. Третье значение координаты z может использоваться при построении экземпляров, но не влияет на геометрический анализ. Все операции выполняются в плоскости xy.

Это можно проверить с помощью:

from shapely.geometry import LineString, Polygon

l = LineString([[1,0.5,0.5],[3,0.5,0.5]])
p = Polygon([[1.2,0.0,0.],[2.2,1.0,0.],[2.8,0.5,1.]])
print(l.intersection(p))
#LINESTRING Z (1.7 0.5 0.25, 2.8 0.5 1)

l = LineString([[1,0.5],[3,0.5]])
p = Polygon([[1.2,0.0],[2.2,1.0],[2.8,0.5]])
print(l.intersection(p))
#LINESTRING (1.7 0.5, 2.8 0.5)

или даже:

from shapely.geometry import LineString, Polygon

l = LineString([[1,0.5,0],[3,0.5,0]])
p = Polygon([[1.2,0.0,1],[2.2,1.0,1],[2.8,0.5,1]])
print(l.intersects(p))
#True (even though the objects are in different z-planes)