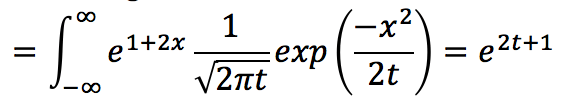Matlab не может вычислить бесконечный интеграл?
Всем привет. Поэтому я изучаю стохастическое исчисление, и иногда нам нужно вычислить интеграл (от -infinity до + бесконечность) для некоторого сложного распределения. В этом случае это было
с ответом справа. Это код, который я поместил в Matlab (и у меня есть символический набор математических инструментов), который Matlab просто не может обработать:
>> syms x t
>> f = exp(1+2*x)*(1/((2*pi*t)^0.5))*exp(-(x^2)/(2*t))
>> int(f,-inf,inf)
ans =
-((2^(1/2)*pi^(1/2)*exp(2*t + 1)*limit(erf((2^(1/2)*((x*1i)/t - 2i))/(2*(-1/t)^(1/2))), x, -Inf)*1i)/(2*(-1/t)^(1/2)) - (2^(1/2)*pi^(1/2)*exp(2*t + 1)*limit(erf((2^(1/2)*((x*1i)/t - 2i))/(2*(-1/t)^(1/2))), x, Inf)*1i)/(2*(-1/t)^(1/2)))/(2*pi*t)^(1/2)
Этот ответ в конце выглядит как бессмыслица, в то время как Wolfram (через их бесплатный инструмент) дает мне ответ, который есть на картинке выше. Я упускаю что-то фундаментальное в таких интеграциях в matlab, которые не рассматриваются на основных страницах математики? Кто-нибудь, пожалуйста, помогите мне понять, где я иду неправильно?
1 ответ
Чтобы объяснить происходящее, нам понадобится немного теории:
Символьные системы, такие как Matlab или Mathematica, вычисляют интегралы символически с помощью алгоритма Риша (да, есть метод для механического вычисления интегралов, как и производных).
Однако алгоритмы Риша работают иначе, чем правила вывода. Строго говоря, это не алгоритм, а полуалгоритм. Это не детерминированный (как алгоритмы).
Этот (полу) алгоритм выполняет серию преобразований входного выражения (того, которое нужно интегрировать), и в определенной точке он требует спросить, равно ли преобразованное выражение нулю, потому что, если бы оно было равно нулю, оно не могло продолжаться. (вход не интегрируется с использованием конечного набора членов).
Проблема (и причина "полуалгоритмичности") в том, что (на первый взгляд простое) уравнение:
E = 0
Является ли indecidable (его также называют проблему постоянной). Это означает, что не может существовать формального метода решения постоянной проблемы для любого выражения E. Конечно, мы знаем, как решить постоянную проблему для конкретных форм выражения E (то есть многочленов), но решить проблему невозможно. для общего случая.
Это также означает, что алгоритм Риша не может быть идеальным (будучи способным решить любой интеграл, интегрируемый в конечных терминах). Другими словами, алгоритм Риша будет столь же мощным, как наша способность решать постоянную проблему для как можно большего числа форм выражения E, но теряет всякую надежду на решение для общего случая.
Различные символьные системы имеют похожие, но разные методы решения уравнений (и, следовательно, постоянную проблему), это объясняет, почему некоторые из них могут "решать" разные наборы интегралов, чем другие.
И обобщение, поскольку никакая символическая система никогда не сможет решить постоянную задачу для общего случая, она также не сможет решить какой-либо интеграл (интегрируемый в конечных членах).
Второй параметр int() должна быть переменная, в которую вы интегрируете (которая выглядит как t в этом случае):
syms x t
f = exp(1+2*x)*(1/((2*pi*t)^0.5))*exp(-(x^2)/(2*t))
int(f,'t',-inf,inf) % <- integrate over t