МОДЕЛЬ GARCH с экзогенными переменными в условном среднем и дисперсии

Question

Мне нужна помощь в написании уравнения GARCH с экзогенными переменными вручную. Я могу написать условное среднее и уравнения условной дисперсии, но не с экзогенными переменными. Установленная модель GARCH представляет собой модель AR(1)-GARCH(1,1). Это то, что я до сих пор:

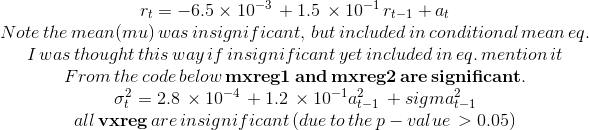
Мне нужна помощь в добавлении mxreg1 и mxreg2 (значимых экзогенных переменных) в уравнение условного среднего. Спасибо!

Если вам трудно ответить на этот вопрос, потому что это похоже на написанное от руки уравнение, вы можете приложить все усилия и загрузить изображение читаемой версии условного среднего уравнения. Спасибо!

*---------------------------------*
*          GARCH Model Fit        *
*---------------------------------*

Conditional Variance Dynamics   
-----------------------------------
GARCH Model : fGARCH(1,1)
fGARCH Sub-Model    : GARCH
Mean Model  : ARFIMA(1,0,0)
Distribution    : norm 

Optimal Parameters
------------------------------------
        Estimate  Std. Error  t value Pr(>|t|)
mu     -0.006505    0.009810 -0.66311 0.507258
ar1     0.149542    0.044502  3.36030 0.000779
mxreg1  0.372466    0.054183  6.87422 0.000000
mxreg2 -0.000754    0.000249 -3.02629 0.002476
mxreg3  0.000749    0.000514  1.45800 0.144840
mxreg4  0.000003    0.000006  0.50995 0.610085
mxreg5  0.062401    0.080066  0.77937 0.435760
omega   0.000276    0.000017 15.95469 0.000000
alpha1  0.119026    0.023418  5.08266 0.000000
beta1   0.785459    0.032615 24.08273 0.000000
vxreg1  0.000000    0.001602  0.00000 1.000000
vxreg2  0.000000    0.000010  0.00000 1.000000
vxreg3  0.000000    0.000021  0.00000 1.000000
vxreg4  0.000000    0.000000  0.00000 1.000000
vxreg5  0.001912    0.003569  0.53563 0.592212

Answer 1

Я работал над моделью ARMAX и считаю, что тот же коэффициент можно применить к уравнению условного возврата модели Гарча с экзогенными переменными. Чтобы добавить одну ковариату, добавьте ßYt к уравнению условного возврата. Для более чем одного ковариата он будет иметь вид ß(Yt + Yt-1 +... Yt-b), где "b" - число экзогенных переменных.