Как определить, находится ли точка внутри скошенного конического усеченного конуса

Question

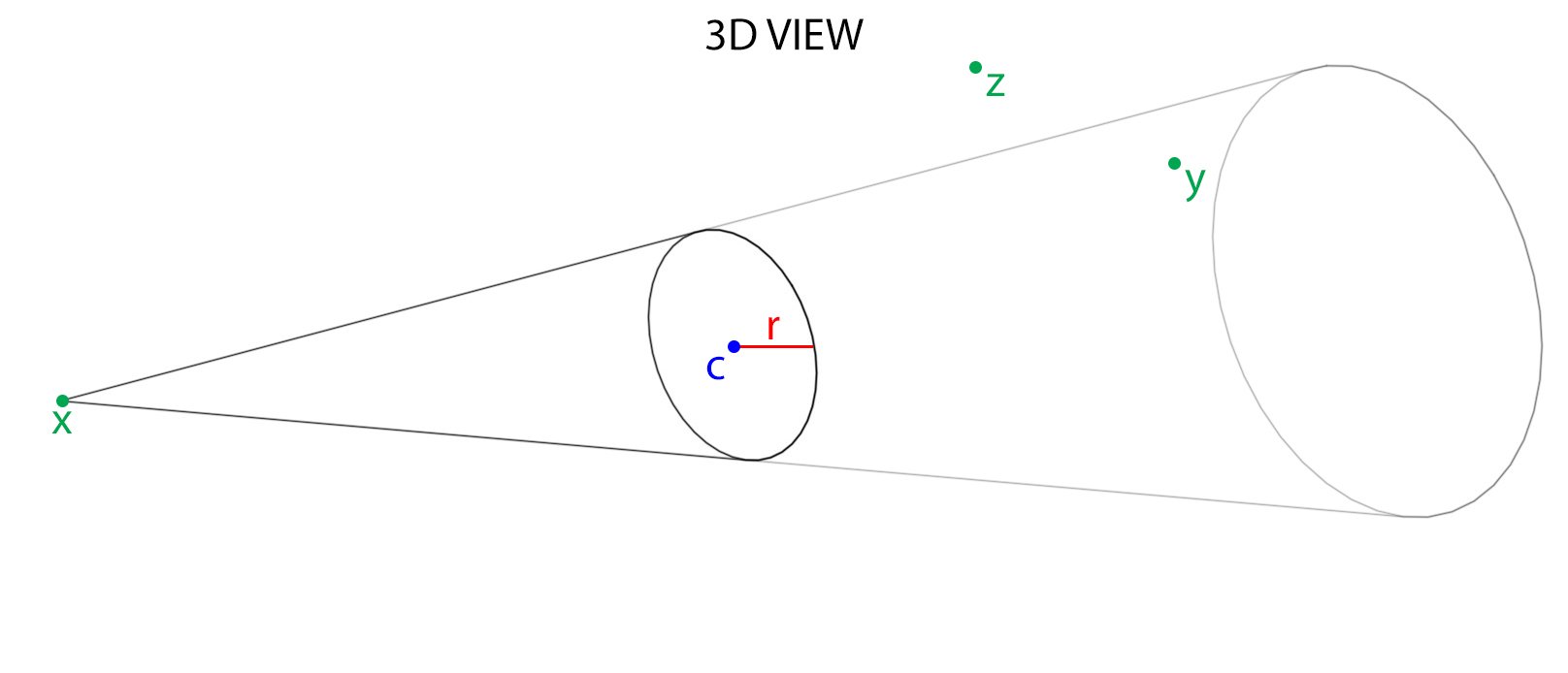
Я пытаюсь выяснить, находится ли точка внутри эллипсоидального конуса, образованного между точкой и окружностью в трехмерном пространстве. Конус эллипсоидальный, потому что точка не перпендикулярна центру круга. Смотрите схему ниже:

Итак, я знаю:

1. Положение точки, образующей вершину конуса: х
2. Расположение центра круга: c
3. Радиус круга: г
4. Расположение различных точек, которые я хочу определить, находятся ли они внутри конуса: y, z

Вот вид сверху той же диаграммы:

Меня не волнует основание конуса - я хочу, чтобы точки внутри конуса были эффективно растянуты до бесконечности.

Я нашел формулы для определения того, находится ли точка в конусе эллипсоида по заданной большой / малой оси, но с трудом решаю, как это сделать, когда конус эллипсоида образован из круга под углом.

Спасибо за любую помощь!

Answer 1

С помощью коники вы, вероятно, могли бы определить расстояние от оси и полуфинала и минора и вычислить его напрямую. Сложнее какой-то произвольной формы.

Если конус имеет точку в направлении оси Z, и вы знаете точку в XYZ... тогда вы сможете нарисовать эллипс на этом конкретном уровне Z. Может быть, нарисовать его с 360 сегментами.

Когда у вас есть точка и эллипс, вы можете проверить сегмент эллипса, чтобы увидеть, есть ли пересечение в X & Y.

Представление круга в 0,0,0 с радиусом 1. А в точке 0,0,0 есть 2Y пересечения в +/- 90 градусов и 2 X пересечения, происходящие в 0 и 180

Если точка равна 2,0,0, у вас все еще есть 2 пересечения в X, но они слева, и вы хотите одно слева и одно справа.

Нулевые пересечения означают. Что ты за обручем.

Повторите через 360 сегментов и определите, как обрабатывать точки "на линии" и насколько близко "на".