Построение двухмерной функции как поверхности в трехмерном пространстве с помощью `Plots.jl`

Question

У меня есть следующая проблема при построении Plots.jl, Мне нравится рисовать функцию Розенброка

rosenbrock(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

как поверхность, которая ожидает 2d Tuple{Float64,Float64} в качестве ввода.

Что я мог придумать, это следующее:

using Plots
gr()

rosenbrock(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

ts = linspace(-1.0, 1.0, 100)
x = ts
y = map(rosenbrock, [(x, z) for (x,z) in zip(ts,ts)])
z = map(rosenbrock, [(x, y) for (x,y) in zip(ts,ts)])
# plot(x, x, z)
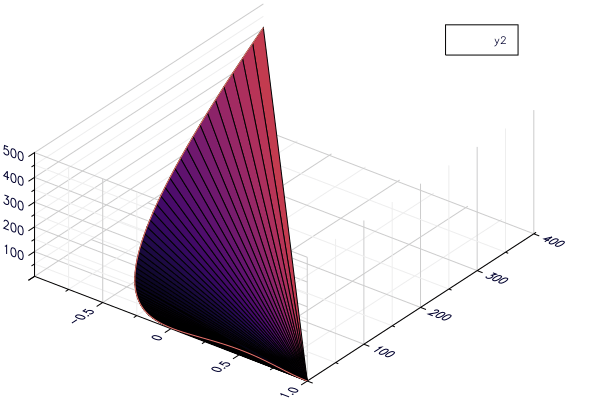
plot(x, y, z, st = [:surface, :contourf])

что дает этот участок:

Я думаю, что перепутал некоторые измерения, но я не вижу, в чем я ошибся.

Должен ли я вложить расчет отображений для y а также x получить результат?

Answer 1

После быстрого изучения функции Розенброка я нашел и исправил меня, если я ошибаюсь, но вам нужно указать y-вектор вы не должны вложить его в z или что-то в этом роде Кто-то еще пробовал то же самое, что показано здесь, но с использованием графиков

решение заключается в следующем, как это сделал Патрик Кофод Могенсен

using Plots

function rosenbrock(x::Vector)
  return (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2
end

default(size=(600,600), fc=:heat)
x, y = -1.5:0.1:1.5, -1.5:0.1:1.5
z = Surface((x,y)->rosenbrock([x,y]), x, y)
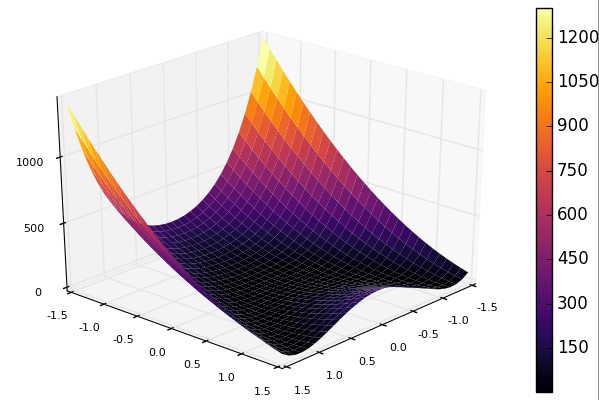
surface(x,y,z, linealpha = 0.3)

Это приводит к

Примечание

Я рад, что я искал это, так как я искал 3D-плоттер для Джулии, кроме PyPlot (так как это может быть немного сложнее настроить для пользователей моей программы), и это даже выглядит лучше, и изображения могут быть поворачивается.