Как сделать ограничения пути, используя Prolog CLP FD?
Я пытаюсь использовать программирование ограничений через Prolog CLP FD для решения предложенной головоломки. Эта головоломка состоит из следующих простых правил:
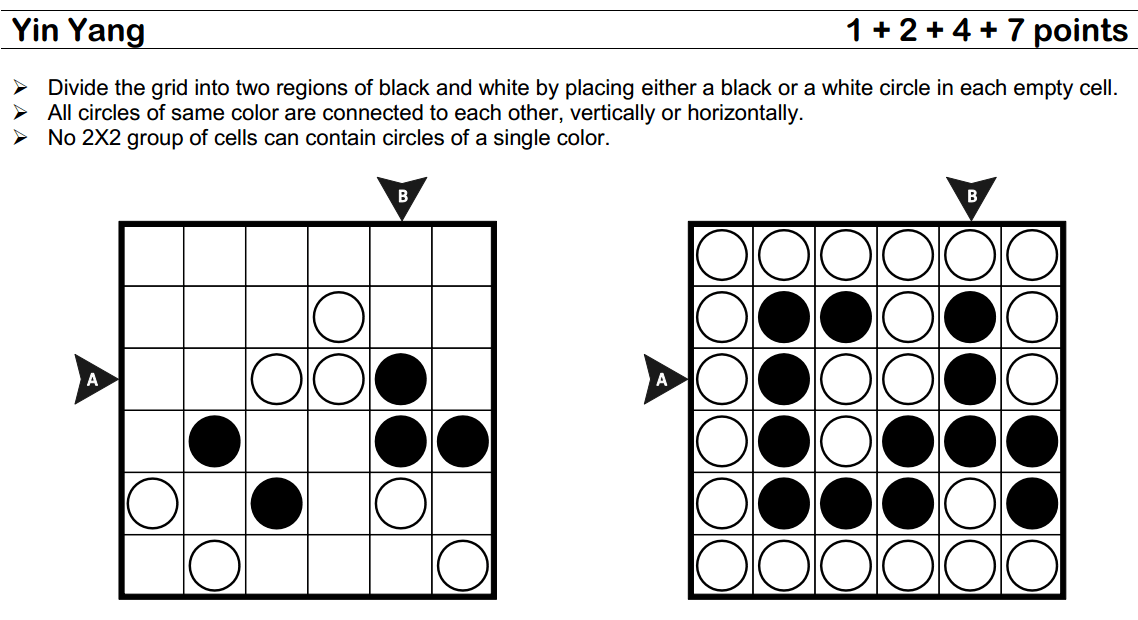
Теперь в своем коде я уже рассмотрел ограничения для сетки 2x2 И то, что один элемент ДОЛЖЕН быть подключен по крайней мере к одному и тому же цвету.
Проблема в том, что я не могу найти способ построить ограничение, которое говорит, что одна часть ДОЛЖНА иметь ПУТЬ (быть подключенной) ко всем другим частям того же цвета, не проходя через части противоположного цвета, поэтому я получаю этот вид выходов:
0 0 0 0
0 1 0 1
0 1 0 1
0 1 0 0
0 0 0 0
0 1 0 1
0 1 0 1
0 1 0 1
где 1 не все связаны друг с другом.
Как я могу написать этот вид графических ограничений в CLP FD?
РЕДАКТИРОВАТЬ: я использую SICStus Prolog.
2 ответа
Чтобы перефразировать вашу ситуацию, чтобы мы могли более четко подумать об этом:
- вы уже можете генерировать ответы
- но ответы в настоящее время слишком общие.
Чтобы сделать вашу программу более конкретной, вы должны найти условие, которое в настоящее время нарушается в одном из сгенерированных вами ответов, но которое должно выполняться в каждом решении, а затем выразить это условие с помощью ограничений.
Например, рассмотрим еще раз ваш случай:
0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1
Какое условие здесь нарушено? Очевидно, что 1 кусочки не по пути. Но описание полного пути с помощью CLP(FD) чрезвычайно утомительно, и, поскольку это, по-видимому, взято из экзаменационного или домашнего задания, возникает мысль, что существует простой локальный критерий для выражения желаемого условия.
Под "местным" я подразумеваю, что вам нужно учитывать только нескольких соседей, а не всю доску.
Итак, рассмотрим еще раз 1 куски. Очевидно, каждый 1 у части есть сосед, который также 1 в этом ответе. Что-то еще? Делает каждый 1 штука есть у 2 соседей? Нет в настоящее время нет. Если каждый 1 часть имеет 2 соседей, которые также 1? Если нет, то сколько исключений допустимо?
Если вы будете думать об этих условиях, вы обязательно получите хорошее решение.
Один совет: иногда ограниченные ограничения полезны в таких задачах. Это означает, что вы можете, например, сказать: B #<==> (X #= Y), и разреши B обозначать ли X #= Y держит. Обратите внимание, что вам может даже не понадобиться это в этом случае.
Кто -нибудь из вас наконец решил эту проблему?
Я очень заинтересован в этой проблеме и хочу увидеть код, если таковой существует.
Я думаю, что схема /1 не может помочь и хочет увидеть использование для решения этой проблемы.