Равномерное распределение n точек по сфере
Я пытаюсь распределить n точек по сфере так, чтобы каждая точка имела "одинаковую" область вокруг нее. По сути, я пытаюсь интегрировать функцию над сферой, оценивая ее в n точках и предполагая, что каждый элемент площади одинаков (и равен 4pi r^2/n).
Мой вопрос очень связан с этим вопросом, но я не могу согласиться с тем, что код, представленный в "принятом" ответе, работает как нужно (см. Прилагаемую фотографию, созданную при выборе R = 1000, nx = ny = 40). Ясно, что мои точки гораздо более сконцентрированы на полюсах и очень не сконцентрированы вдоль экватора.
Какие-либо предложения?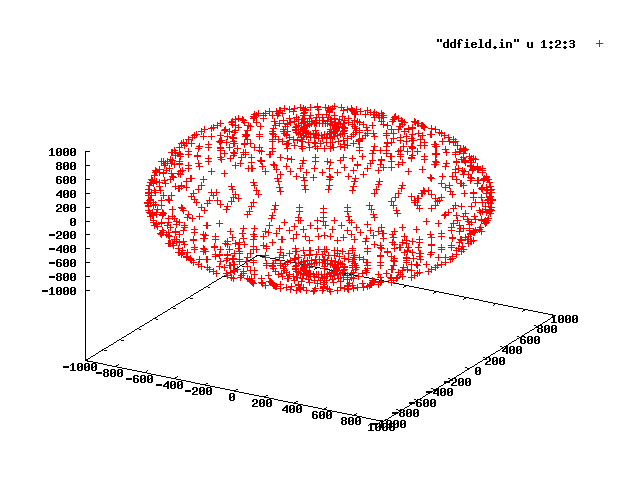
РЕДАКТИРОВАТЬ: Для справки, я нашел какое-то программное обеспечение, которое генерирует сетку таким образом, что каждая точка имеет равную "площадь" вокруг нее (прокрутите вниз, чтобы увидеть равномерное распределение площади по сфере), но вместо того, чтобы реализовать их код, я пошел с меньшими затратами. Подход, отнимающий много времени: я просто перебрал азимутальный и полярный углы ([0,2pi] и [0,pi]) и вычислил "бесконечно малую" площадь каждого патча (da = r^2 sin theta dtheta dphi). Это в основном все, что мне нужно для интеграции по сфере, я просто надеялся, что равномерное распределение не будет таким трудным для реализации.
5 ответов
Исходная информация:
В сфере есть 4 пи стерадианы, это общие "градусы" в сфере, но я использую этот термин только в относительном смысле, потому что стерадианы сильно отличаются от обычных радианов в круге, например, они трехмерны и поэтому твердые Просто считайте их сферическими углами в форме мороженого.
http://en.wikipedia.org/wiki/Steradian предоставляет отличный пример из них.
Они имеют прямое отношение к радиусу, как радианы в круге. 1 стерадиан = 1 единица радиуса в квадрате.
Итак, сначала выясните, сколько предметов нужно нанести на сферу. Пусть это число будет n,sr = стерадианы (единица измерения) = r^2 (радиус в квадрате)
4 pi / n sr = x
x Сколько стерадиан выделяется для каждой точки.
скажем за 4 балла.
4 pi / 4 sr = x
pi sr = x Таким образом, каждая точка получит выделенное пространство pi sr,
Теперь рассмотрим это... так как вы строите точки, мы будем считать, что каждая точка будет размещена в середине выделенного пространства... то есть в середине конусообразной области, что sr является. Теперь вам нужно кое-что обдумать, возможно ли заполнить область полностью кружками? Серьезно, подумай об этом... это не так ли? Сплошные круги всегда оставляют место между ними в определенных местах. Подумайте о футбольном мяче на мгновение. Он построен из форм, которые могут объединиться, чтобы обеспечить равномерное распределение. Смысл этой мысли состоит в том, чтобы вы поняли, что все точки не могут быть точно на определенном расстоянии друг от друга - например, как у круга есть радиус. Тем не менее, центр квадратов футбольного мяча очень близко и равномерно.
Что бы я сделал на вашем месте, это попытался бы написать алгоритм, чтобы определить наиболее эффективную "форму", чтобы поместить каждый из этих "кусочков" выделенного сферического пространства в... как футбольный мяч. В противном случае, я думаю, что это может быть лучшим ответом, который вы получите... 4 pi / n sr = x... нет возможности построить каждую точку, чтобы она находилась на одинаковом расстоянии друг от друга (за исключением определенных конфигураций, т. е. это было бы возможно с особым количеством точек), может существовать алгоритм для поиска всех особые случаи.
Я редактирую этот ответ для уточнения особых случаев, я думаю, что здесь было бы неплохо получить дополнительную информацию. Особые случаи, когда точки находятся на равном расстоянии друг от друга, состоят в том, что они могут образовывать вершины платоновых тел. Есть только 5 основных платонических твердых форм, все остальные сделаны из них.
Прочтите эту страницу для получения дополнительной информации и доказательства этого https://www.uwgb.edu/dutchs/symmetry/platonic.htm
Теперь я не могу взять кредит, я провел небольшое исследование и нашел аналогичный пост https://math.stackexchange.com/questions/279544/return-an-array-of-evenly-distributed-points-on-a-sphere-give-radius-and-origin
Использование формулы многогранника Эйлера http://plus.maths.org/content/eulers-polyhedron-formula
и тот факт, что только три основные фигуры существуют на многогранниках, "треугольниках, квадратах и шестиугольниках", вы можете создать алгоритм для округления числа точек, которые вы хотите построить, до ближайшей формы многогранника и равномерного построения каждой из них.
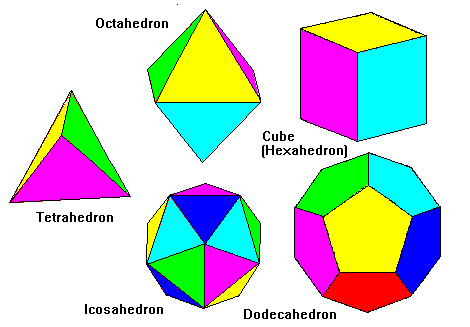
О, и взгляните на эту замечательную статью, она объясняет стерадианы и трехмерные "градусы" гораздо лучше, чем я. http://mathforum.org/library/drmath/view/55358.html
Вот пример алгоритма, который я только что описал в python:
from numpy import random, cos, sin, sqrt, pi
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
def rand_sphere(n):
"""n points distributed evenly on the surface of a unit sphere"""
z = 2 * random.rand(n) - 1 # uniform in -1, 1
t = 2 * pi * random.rand(n) # uniform in 0, 2*pi
x = sqrt(1 - z**2) * cos(t)
y = sqrt(1 - z**2) * sin(t)
return x, y, z
x, y, z = rand_sphere(200)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z)
plt.show()
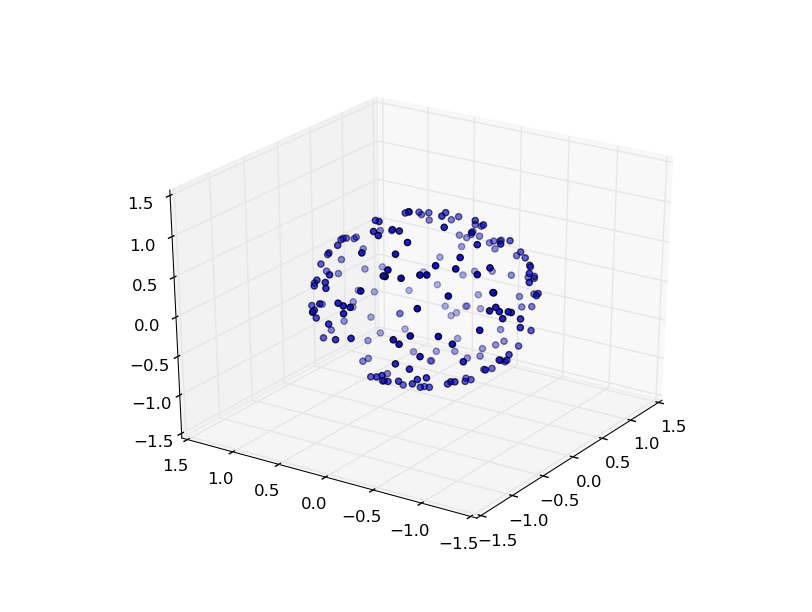
Опять с 10000 баллами:
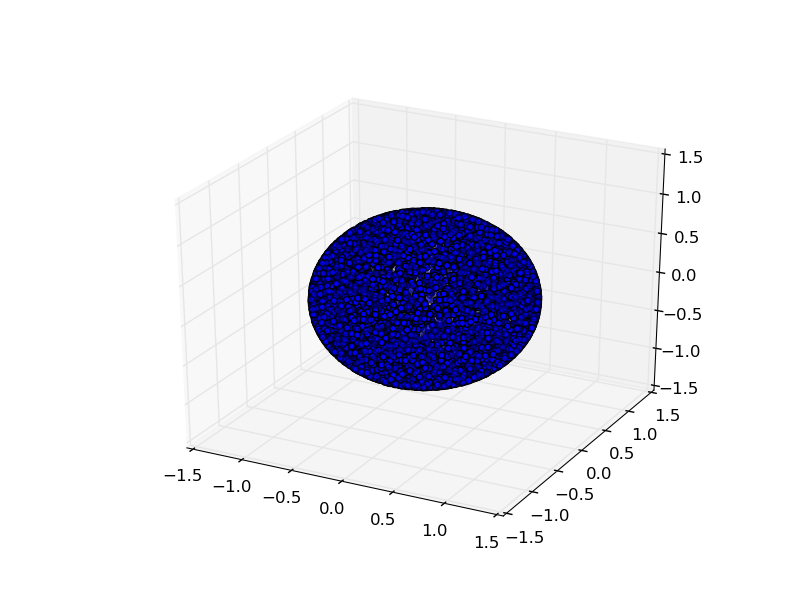
Может быть не так, но если
- установить взаимодействие между двумя точками, поскольку I(a,b) = (ab) / (|ab|)^3, a,b находятся под угрозой как векторы в трехмерном пространстве
- для первых итераций расставьте точки как обычно (на равных угловых расстояниях, как это было упомянуто в посте wim)
- на каждом шаге алгоритма вы будете перемещать каждую точку против градиента суммы I (из 1.), где I рассчитывается только по прямым соседям
- повторяйте 3, пока градиент в каждой точке не станет 0.
алгоритм будет сходиться к конфигурации, что вам нужно. Это отнимает много времени, но вы можете кэшировать результаты для различного количества баллов.
Существует программное обеспечение, которое определяет равномерную пикселизацию сферы таким образом, что каждая точка окружена одинаковым количеством телесных углов. Оформить заказ: http://healpix.jpl.nasa.gov/ Они также предоставляют несколько подпрограмм, чтобы сделать некоторые полезные вычисления в Fortan, C, C++, Python, MathLab, среди других...
Что касается ответа Клика, предпосылка правильна, а формула неверна. Если бы формула была n/4pi, то если бы у вас было 4 балла, результат был бы 4/(4× пи), что составляет 0,3183 (не пи). То, что вы хотите сделать, это взять общее количество стерадианов на сфере (т.е. 4pi) и разделить его на n раз. Эта формула 4pi/ п.