Ограничения для линейной модели с использованием Quadprog для диапазонов / пределов коэффициентов

Question

Я делаю некоторые эксперименты, и я, конечно, знаю, почему ограничение коэффициентов требуется редко, но здесь идет.

В следующих данных я использовал quadprog для решения линейной модели. Обратите внимание, что X1 просто перехват.

X1 <- 1
X2 <- c(4.374, 2.3708, -7.3033, 12.0803, -0.4098, 53.0631, 13.1304, 7.3617, 16.6252, 27.3394)
X3 <- c(2.6423, 2.6284, 36.9398, 15.9278, 18.3124, 54.5039, 3.764, 19.0552, 25.4906, 13.0112)
X4 <- c(4.381, 3.144, 9.506, 15.329, 21.008, 38.091, 22.399, 13.223, 17.419, 19.87)
X <- as.matrix(cbind(X1,X2,X3,X4))
Y <- as.matrix(c(37.7,27.48,24.08,25.97,16.65,73.77,45.10,53.35,61.95,71.15))
M1 <- solve.QP(t(X) %*% X, t(Y) %*% X, matrix(0, 4, 0), c())$solution

Задача состоит в том, чтобы ограничить определенные коэффициенты. Я знаю, что я должен изменить параметры Amet и bvac (согласно линейной регрессии с ограничениями на коэффициенты). Однако я не уверен, как его настроить, чтобы были соблюдены следующие ограничения.

Выходные данные читаются как [1] ​​37.3468790 1.2872473 -0.0177749 -0.5988443, где значения будут прогнозируемыми подобранными значениями X1, X2, X3 и X4.

Ограничения (при условии)…

X2 <= .899

0 <= X3 <= .500

0 <= X4 <= .334

Answer 1

Просто чтобы уточнить: вы даете ожидаемый результат "где значения будут предсказаны подогнанные значения X1, X2, X3 и X4". Я предполагаю, что вы имеете в виду приблизительные (не установленные) значения параметров.

Это довольно просто реализовать ограниченные параметры при моделировании данных в rstan, rstan интерфейс R для Stan, который, в свою очередь, является вероятностным языком программирования для статистического байесовского вывода.

Вот пример на основе предоставленных вами образцов данных.

1. Во-первых, давайте определимся с нашей моделью. Обратите внимание, что мы ограничиваем параметры beta2, beta3 а также beta4 согласно вашим требованиям

   model <- "
   data {
       int<lower=1> n;   // number of observations
       int<lower=0> k;   // number of parameters
       matrix[n, k] X;   // data
       vector[n] y;      // response
   }
   
   parameters {
       real beta1;                                                  // X1 unconstrained
       real<lower=negative_infinity(), upper=0.899> beta2;          // X2 <= .899
       real<lower=0, upper=0.5> beta3;                              // 0 <= X3 <= 0.5
       real<lower=0, upper=0.334> beta4;                            // 0 <= X4 <= 0.334
       real sigma;                                                  // residuals
   }
   
   model {
       // Likelihood
       y ~ normal(beta1 * X[, 1] + beta2 * X[, 2] + beta3 * X[, 3] + beta4 * X[, 4], sigma);
   }"
   

2. Далее мы подгоняем модель к вашим образцам данных.

   library(rstan)
   rstan_options(auto_write = TRUE)
   options(mc.cores = parallel::detectCores())
   df <- cbind.data.frame(Y, X)
   fit <- stan(
       model_code = model,
       data = list(
           n = nrow(df),
           k = ncol(df[, -1]),
           X = df[, -1],
           y = df[, 1]))
   

3. Наконец, давайте напечатаем оценки параметров аккуратно

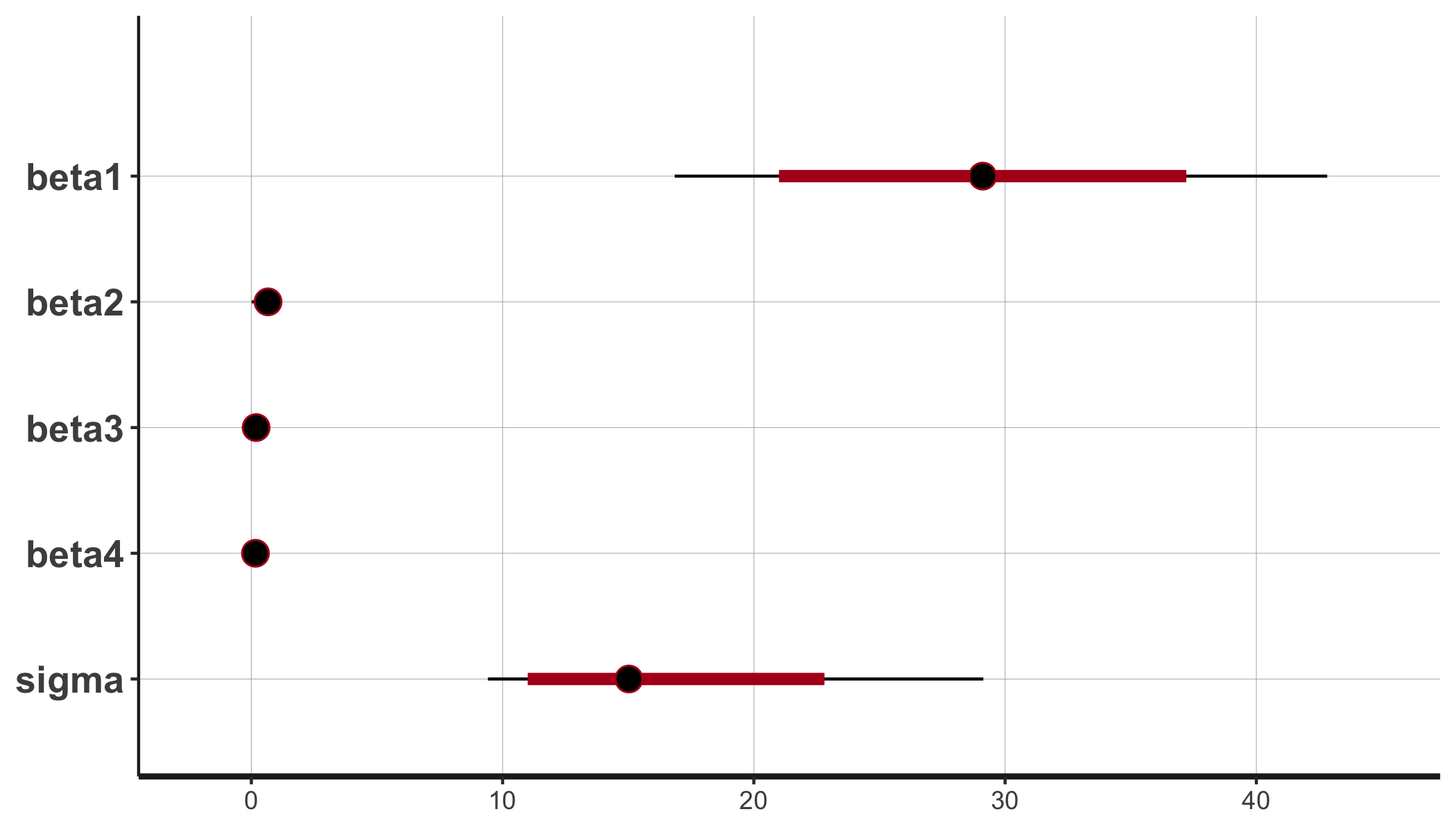
   library(broom)
   tidy(fit, conf.int = TRUE)
   ## A tibble: 5 x 5
   #  term  estimate std.error conf.low conf.high
   #  <chr>    <dbl>     <dbl>    <dbl>     <dbl>
   #1 beta1   29.2      6.53   16.9        42.8
   #2 beta2    0.609    0.234   0.0149      0.889
   #3 beta3    0.207    0.138   0.00909     0.479
   #4 beta4    0.164    0.0954  0.00780     0.326
   #5 sigma   16.2      5.16    9.42       29.1
   

   Мы также можем построить оценки параметров, включая CI.

Обратите внимание, что оценки параметров согласуются с наложенными ограничениями.