Наивный байесовский классификатор - множественные решения
Мне нужно знать, можно ли использовать наивный байесовский классификатор для выработки нескольких решений. Я не смог найти примеров, которые бы подтверждали множество решений. Я новичок в этой области. Итак, я немного растерялся.
На самом деле мне нужно разработать программное обеспечение для распознавания символов. Там мне нужно определить, что это за персонаж. Похоже, байесовский классификатор можно использовать для определения того, является ли данный символ конкретным или нет, но он не может дать никаких других предложений.
Например, если дано изображение "3" (мы думаем, что это "3"), если система не может идентифицировать его как "3". Если для системы кажется "2", система должна вернуть "2".
Идея, которую я имею о наивном байесовском классификаторе, заключается в том, что после обучения данных мы можем спросить систему, является ли данный символ конкретным или нет. Например. Мы рисуем изображение определенного числа и спрашиваем систему: "2" или нет.
Я также заметил, что KNN(k ближайший сосед) дает несколько решений. Символ, данный этому, решает ближайший совместимый символ, указанный в данных тренировки.
Буду очень признателен, если кто-нибудь объяснит мне, можно ли использовать наивный байесовский классификатор для принятия нескольких решений, как указано выше.
2 ответа
Предположение наивного байесовского классификатора состоит в том, что измерения данных независимы (наивная часть) и что модель является генеративной (байесовская часть). Другими словами, вы моделируете, как данные генерируются из состояний мира - P(data|world_state), где world_state может быть продолжением или категориальной переменной (с несколькими классами-категориями). Это работает в отличие от дискриминирующих моделей, которые игнорируют генерацию данных и описывают апостериорную вероятность состояний мира посредством прямого "взлома" данных: P(world_state|data)
Вот шаги, которые вы должны выполнить, чтобы реализовать наивный байесовский классификатор:
1. Моделируйте ваши данные с помощью генеративной модели, например, гауссовского распределения. У каждого класса будет свой гауссов. В наивной модели вы берете произведение гауссиан для каждого измерения данных. В более полной модели размерность гауссиана равна размерности данных.
2. Определите априор для каждого из ваших классов (например, категориальное распределение с одной вероятностью, назначенной каждому классу);
3. Изучите параметры, подгоняя гауссиан к вашим данным;
4. Оцените класс тестовых данных по формуле Байеса:
P(class|data) = P(data|class) * P(class)/P(data); [1]
P(data) = sum_over_classes[P(data|class) * P(class)]; [2]
Первый член в формуле 1 называется апостериорным, второй - вероятностью, а последний - предшествующим. Знаменатель, показанный в [2], часто игнорируется, когда вы вычисляете максимальный апостериор (MAP), который является наиболее вероятным классом, ответственным за генерацию данных. Однако знаменатель очень важен для понимания того, как модели классов работают вместе.
Например, вы можете создать очень сложную порождающую модель для каждого класса, но ваш апостериор будет выглядеть очень просто из-за того, что во время нормализации одна из вероятностей была уменьшена до 0. В этом случае лучше отказаться от байесовского подхода и создать дискриминативная модель с меньшим количеством параметров, чем в генеративной. На приведенной ниже диаграмме вертикальные оси представляют собой вероятности мирового состояния (класса), а горизонтальные оси представляют данные. 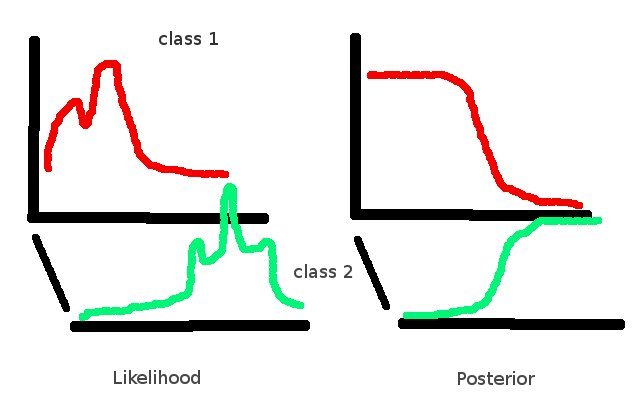
Байесовский классификатор должен давать вероятность того, что элемент будет принадлежать каждому из нескольких классов. Определенно возможно иметь более двух классов.
С вероятностями для классов, вы, как правило, хотите принять решение, которое может быть сделано, например, путем выбора наиболее вероятного класса. Это может быть причиной того, что вы видите только одну возможность.