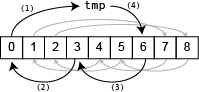Самый быстрый алгоритм для сдвига окружности массива N размера для позиции М
Какой самый быстрый алгоритм для массива сдвига окружности для M позиций?
Например, [3 4 5 2 3 1 4] сдвиг M = 2 позиции должен быть [1 4 3 4 5 2 3],
Большое спасибо.
26 ответов
Если вы хотите использовать время O(n) и не использовать лишнюю память (поскольку был указан массив), используйте алгоритм из книги Джона Бентли "Программирование жемчужин, 2-е издание". Это меняет местами все элементы дважды. Не так быстро, как использование связанных списков, но использует меньше памяти и концептуально прост.
shiftArray( theArray, M ):
size = len( theArray )
assert( size > M )
reverseArray( theArray, 0, size - 1 )
reverseArray( theArray, 0, M - 1 )
reverseArray( theArray, M, size - 1 )
reverseArray (anArray, startIndex, endIndex) меняет порядок элементов от startIndex до endIndex включительно.
Оптимальным решением
Вопрос задан быстрее всех. Реверсировать три раза проще всего, но каждый элемент перемещается ровно дважды, занимает O(N) времени и O(1) пространства. Можно сместить массив по кругу, перемещая каждый элемент ровно один раз, также за время O(N) и пространство O(1).
идея
Мы можем сместить круг по длине N=9 от M=1 с одним циклом:
tmp = arr[0]; arr[0] = arr[1]; ... arr[7] = arr[8]; arr[8] = tmp;
И если N=9, M=3 мы можем сдвигать круг с тремя циклами:
tmp = arr[0]; arr[0] = arr[3]; arr[3] = tmp;tmp = arr[1]; arr[1] = arr[4]; arr[4] = tmp;tmp = arr[2]; arr[2] = arr[5]; arr[5] = tmp;
Обратите внимание, что каждый элемент читается один раз и записывается один раз.
Схема смещения N=9, M=3
Первый цикл показан черным цветом с цифрами, указывающими порядок операций. Второй и третий циклы показаны серым цветом.
Требуемое количество циклов - Величайший общий делитель (GCD) N а также M, Если GCD равен 3, мы запускаем цикл в каждом из {0,1,2}, Расчет GCD быстрый с двоичным алгоритмом GCD.
Пример кода:
// n is length(arr)
// shift is how many place to cycle shift left
void cycle_shift_left(int arr[], int n, int shift) {
int i, j, k, tmp;
if(n <= 1 || shift == 0) return;
shift = shift % n; // make sure shift isn't >n
int gcd = calc_GCD(n, shift);
for(i = 0; i < gcd; i++) {
// start cycle at i
tmp = arr[i];
for(j = i; 1; j = k) {
k = j+shift;
if(k >= n) k -= n; // wrap around if we go outside array
if(k == i) break; // end of cycle
arr[j] = arr[k];
}
arr[j] = tmp;
}
}
Код на C для любого типа массива:
// circle shift an array left (towards index zero)
// - ptr array to shift
// - n number of elements
// - es size of elements in bytes
// - shift number of places to shift left
void array_cycle_left(void *_ptr, size_t n, size_t es, size_t shift)
{
char *ptr = (char*)_ptr;
if(n <= 1 || !shift) return; // cannot mod by zero
shift = shift % n; // shift cannot be greater than n
// Using GCD
size_t i, j, k, gcd = calc_GCD(n, shift);
char tmp[es];
// i is initial starting position
// Copy from k -> j, stop if k == i, since arr[i] already overwritten
for(i = 0; i < gcd; i++) {
memcpy(tmp, ptr+es*i, es); // tmp = arr[i]
for(j = i; 1; j = k) {
k = j+shift;
if(k >= n) k -= n;
if(k == i) break;
memcpy(ptr+es*j, ptr+es*k, es); // arr[j] = arr[k];
}
memcpy(ptr+es*j, tmp, es); // arr[j] = tmp;
}
}
// cycle right shifts away from zero
void array_cycle_right(void *_ptr, size_t n, size_t es, size_t shift)
{
if(!n || !shift) return; // cannot mod by zero
shift = shift % n; // shift cannot be greater than n
// cycle right by `s` is equivalent to cycle left by `n - s`
array_cycle_left(_ptr, n, es, n - shift);
}
// Get Greatest Common Divisor using binary GCD algorithm
// http://en.wikipedia.org/wiki/Binary_GCD_algorithm
unsigned int calc_GCD(unsigned int a, unsigned int b)
{
unsigned int shift, tmp;
if(a == 0) return b;
if(b == 0) return a;
// Find power of two divisor
for(shift = 0; ((a | b) & 1) == 0; shift++) { a >>= 1; b >>= 1; }
// Remove remaining factors of two from a - they are not common
while((a & 1) == 0) a >>= 1;
do
{
// Remove remaining factors of two from b - they are not common
while((b & 1) == 0) b >>= 1;
if(a > b) { tmp = a; a = b; b = tmp; } // swap a,b
b = b - a;
}
while(b != 0);
return a << shift;
}
Редактировать: этот алгоритм также может иметь лучшую производительность по сравнению с обращением массива (когда N большой и M небольшой) из-за локальности кэша, так как мы выполняем цикл по массиву небольшими шагами.
Последнее замечание: если ваш массив маленький, тройной обратный процесс прост. Если у вас большой массив, стоит потратить на разработку GCD, чтобы уменьшить количество ходов в 2 раза. Ссылка: http://www.geeksforgeeks.org/array-rotation/
Это просто вопрос представительства. Сохраняйте текущий индекс как целочисленную переменную, а при обходе массива используйте оператор по модулю, чтобы знать, когда обернуться. Сдвиг тогда только изменяет значение текущего индекса, оборачивая его вокруг размера массива. Это конечно O(1).
Например:
int index = 0;
Array a = new Array[SIZE];
get_next_element() {
index = (index + 1) % SIZE;
return a[index];
}
shift(int how_many) {
index = (index+how_many) % SIZE;
}
Установите его с помощью указателей, и это займет почти время. Каждый элемент указывает на следующий, а "последний" (нет последнего; в конце концов, вы сказали, что он был круглым) указывает на первый. Один указатель на "начало" (первый элемент) и, возможно, длину, и у вас есть свой массив. Теперь, чтобы сделать вашу смену, вы просто проведете указатель начала по кругу.
Попросите хороший алгоритм, и вы получите разумные идеи. Спросите быстрее, и вы получите странные идеи!
Этот алгоритм работает в O(n) времени и O(1) пространстве. Идея состоит в том, чтобы проследить каждую циклическую группу в смене (пронумерованы как nextGroup переменная).
var shiftLeft = function(list, m) {
var from = 0;
var val = list[from];
var nextGroup = 1;
for(var i = 0; i < list.length; i++) {
var to = ((from - m) + list.length) % list.length;
if(to == from)
break;
var temp = list[to];
list[to] = val;
from = to;
val = temp;
if(from < nextGroup) {
from = nextGroup++;
val = list[from];
}
}
return list;
}
def shift(nelements, k):
result = []
length = len(nelements)
start = (length - k) % length
for i in range(length):
result.append(nelements[(start + i) % length])
return result
Этот код хорошо работает даже при отрицательном сдвиге k
Вот простая и эффективная общая функция поворота на месте в C++, менее 10 строк.
который взят из моего ответа на другой вопрос. Как вращать массив?
#include <iostream>
#include <vector>
// same logic with STL implementation, but simpler, since no return value needed.
template <typename Iterator>
void rotate_by_gcd_like_swap(Iterator first, Iterator mid, Iterator last) {
if (first == mid) return;
Iterator old = mid;
for (; mid != last;) {
std::iter_swap(first, mid);
++first, ++mid;
if (first == old) old = mid; // left half exhausted
else if (mid == last) mid = old;
}
}
int main() {
using std::cout;
std::vector<int> v {0,1,2,3,4,5,6,7,8,9};
cout << "before rotate: ";
for (auto x: v) cout << x << ' '; cout << '\n';
int k = 7;
rotate_by_gcd_like_swap(v.begin(), v.begin() + k, v.end());
cout << " after rotate: ";
for (auto x: v) cout << x << ' '; cout << '\n';
cout << "sz = " << v.size() << ", k = " << k << '\n';
}
C arrayShiftRight функция. Если shift отрицателен, функция сдвигает массив влево. Он оптимизирован для меньшего использования памяти. Время работы O(n).
void arrayShiftRight(int array[], int size, int shift) {
int len;
//cut extra shift
shift %= size;
//if shift is less then 0 - redirect shifting left
if ( shift < 0 ) {
shift += size;
}
len = size - shift;
//choosing the algorithm which needs less memory
if ( shift < len ) {
//creating temporary array
int tmpArray[shift];
//filling tmp array
for ( int i = 0, j = len; i < shift; i++, j++ ) {
tmpArray[i] = array[j];
}
//shifting array
for ( int i = size - 1, j = i - shift; j >= 0; i--, j-- ) {
array[i] = array[j];
}
//inserting lost values from tmp array
for ( int i = 0; i < shift; i++ ) {
array[i] = tmpArray[i];
}
} else {
//creating temporary array
int tmpArray[len];
//filling tmp array
for ( int i = 0; i < len; i++ ) {
tmpArray[i] = array[i];
}
//shifting array
for ( int i = 0, j = len; j < size; i++, j++ ) {
array[i] = array[j];
}
//inserting lost values from tmp array
for ( int i = shift, j = 0; i < size; i++, j++ ) {
array[i] = tmpArray[j];
}
}
}
Очень простое решение. Это очень быстрый способ, здесь я использую временный массив с тем же размером или оригиналом и присоединяю к исходной переменной в конце. Этот метод использует O(n) временную сложность и O(n) пространственную сложность, и его очень просто реализовать.
int[] a = {1,2,3,4,5,6};
int k = 2;
int[] queries = {2,3};
int[] temp = new int[a.length];
for (int i = 0; i<a.length; i++)
temp[(i+k)%a.length] = a[i];
a = temp;
Теоретически, самый быстрый цикл выглядит так:
if (begin != middle && middle != end)
{
for (i = middle; ; )
{
swap(arr[begin++], arr[i++]);
if (begin == middle && i == end) { break; }
if (begin == middle) { middle = i; }
else if (i == end) { i = middle; }
}
}
На практике вы должны профилировать его и посмотреть.
Это должно работать для кругового смещения арри: Input: { 1, 2, 3, 5, 6, 7, 8 }; Выходное значение присутствует в массиве после forloops: {8,7,1,2,3,5,6,8,7}
class Program
{
static void Main(string[] args)
{
int[] array = { 1, 2, 3, 5, 6, 7, 8 };
int index = 2;
int[] tempArray = new int[array.Length];
array.CopyTo(tempArray, 0);
for (int i = 0; i < array.Length - index; i++)
{
array[index + i] = tempArray[i];
}
for (int i = 0; i < index; i++)
{
array[i] = tempArray[array.Length -1 - i];
}
}
}
Ответ @IsaacTurner (C) /questions/7765884/samyij-byistryij-algoritm-dlya-sdviga-okruzhnosti-massiva-n-razmera-dlya-pozitsii-m/7765892#7765892
и ответ @SomeStrangeUser (Java): /questions/30028618/krugovoe-smeschenie-vlevo-massiva-na-n-pozitsij-v-java/30028625#30028625
предоставить простой алгоритм времени O(N) и пространства O(1), который отвечает на вопрос и требует назначений ровно N элементов. Однако я считаю (и кто-нибудь поправит меня, если я ошибаюсь), что вычисление gcd между N и M не является необходимым; Достаточно просто подсчета количества элементов, которые мы поместили на их правильные места. Это связано с тем, что после того, как мы поместили элемент на его правильное место, мы гарантируем, что нам больше не придется обращаться к нему ни в текущем, ни в последующих циклах.
Вот реализация Python 3 с этим дополнительным упрощением:
# circle shift an array to the left by M
def arrayCircleLeftShift(a, M):
N = len(a)
numAccessed = 0
cycleIdx = 0
while numAccessed != N:
idx = cycleIdx
swapIdx = (idx + M) % N
tmp = a[idx]
while swapIdx != cycleIdx:
a[idx] = a[swapIdx]
numAccessed += 1
idx = swapIdx
swapIdx = (idx + M) % N
a[idx] = tmp
numAccessed += 1
cycleIdx += 1
Я знаю, что это старый пост, однако вот оптимальное решение в O(n): каждый элемент перемещается ровно один раз, и дополнительное пространство не требуется. Оно очень похоже на решение, предложенное Исааком Тернером, но не требует вычисления НОД.
public static void shiftArray(int[] A, int k) {
if (A.length == 0) {
return;
}
k = k % A.length;
k = (k + A.length) % A.length; // ensure k is positive
if (k == 0) {
return;
}
int i = 0, i0 = 0;
int x = A[0];
for (int u = 0; u < A.length; u++) { // count number of shifted elements
int j = (i - k + A.length) % A.length; // ensure modulo is positive
if (j == i0) { // end of a (sub-)cycle, advance to next one
A[i] = x;
x = A[i = ++i0];
} else {
A[i] = A[j];
i = j;
}
}
}
Этот метод сделает эту работу:
public static int[] solution1(int[] A, int K) {
int temp[] = new int[A.length];
int count = 0;
int orignalItration = (K < A.length) ? K :(K%A.length);
for (int i = orignalItration; i < A.length; i++) {
temp[i] = A[count++];
}
for (int i = 0; i < orignalItration; i++) {
temp[i] = A[count++];
}
return temp;
}
static int [] shift(int arr[], int index, int k, int rem)
{
if(k <= 0 || arr == null || arr.length == 0 || rem == 0 || index >= arr.length)
{
return arr;
}
int temp = arr[index];
arr = shift(arr, (index+k) % arr.length, k, rem - 1);
arr[(index+k) % arr.length] = temp;
return arr;
}
Пример Ruby:
def move_cyclic2 array, move_cnt
move_cnt = array.length - move_cnt % array.length
if !(move_cnt == 0 || move_cnt == array.length)
array.replace( array[move_cnt..-1] + array[0...move_cnt] )
end
end
Посмотрите это, если вы заинтересованы в реализации Java:
Вот реализация С++. Временная сложность O(n), пространственная сложность O(1)
M = M % theArray.size();
reverse(theArray.begin(), theArray.end());
reverse(nums.begin(), theArray.begin()+ M);
reverse(theArray.begin()+ M, theArray.end());
Вот еще одна реализация с использованием техники циклических замен. Временная сложность O(n), пространственная сложность O(1).
void rotate(vector<int>& nums, int k) {
int n = nums.size();
int start = 0;
int count = 0;
while(count < n) {
int temp = nums[start];
int i = (start + k) % n;
while(i != start) {
int temp2 = nums[i];
nums[i] = temp;
temp = temp2;
i = (i + k) % n;
count++;
}
nums[i] = temp;
count++;
start++;
}
}
Вот мое решение на Java, которое принесло мне 100% баллов за задание и 100% правильности в Codility:
class Solution {
public int[] solution(int[] A, int K) {
// write your code in Java SE 8
if (A.length > 0)
{
int[] arr = new int[A.length];
if (K > A.length)
K = K % A.length;
for (int i=0; i<A.length-K; i++)
arr[i+K] = A[i];
for (int j=A.length-K; j<A.length; j++)
arr[j-(A.length-K)] = A[j];
return arr;
}
else
return new int[0];
}
}
Обратите внимание: несмотря на for циклы, итерация по всему массиву выполняется только один раз.
Версия Swift 4 для перемещения массива влево.
func rotLeft(a: [Int], d: Int) -> [Int] {
var result = a
func reverse(start: Int, end: Int) {
var start = start
var end = end
while start < end {
result.swapAt(start, end)
start += 1
end -= 1
}
}
let lenght = a.count
reverse(start: 0, end: lenght - 1)
reverse(start: lenght - d, end: lenght - 1)
reverse(start: 0, end: lenght - d - 1)
return result
}
Например, если входной массив a = [1, 2, 3, 4, 5]и смещение влево d = 4, тогда результат будет [5, 1, 2, 3, 4]
Мой друг, шутя, спросил меня, как сдвинуть массив, я придумал это решение (см. Ссылку на ideone), теперь я видел ваше, кто-то кажется немного эзотерическим.
Посмотрите здесь.
#include <iostream>
#include <assert.h>
#include <cstring>
using namespace std;
struct VeryElaboratedDataType
{
int a;
int b;
};
namespace amsoft
{
namespace inutils
{
enum EShiftDirection
{
Left,
Right
};
template
<typename T,size_t len>
void infernalShift(T infernalArray[],int positions,EShiftDirection direction = EShiftDirection::Right)
{
//assert the dudes
assert(len > 0 && "what dude?");
assert(positions >= 0 && "what dude?");
if(positions > 0)
{
++positions;
//let's make it fit the range
positions %= len;
//if y want to live as a forcio, i'l get y change direction by force
if(!direction)
{
positions = len - positions;
}
// here I prepare a fine block of raw memory... allocate once per thread
static unsigned char WORK_BUFFER[len * sizeof(T)];
// std::memset (WORK_BUFFER,0,len * sizeof(T));
// clean or not clean?, well
// Hamlet is a prince, a prince does not clean
//copy the first chunk of data to the 0 position
std::memcpy(WORK_BUFFER,reinterpret_cast<unsigned char *>(infernalArray) + (positions)*sizeof(T),(len - positions)*sizeof(T));
//copy the second chunk of data to the len - positions position
std::memcpy(WORK_BUFFER+(len - positions)*sizeof(T),reinterpret_cast<unsigned char *>(infernalArray),positions * sizeof(T));
//now bulk copy back to original one
std::memcpy(reinterpret_cast<unsigned char *>(infernalArray),WORK_BUFFER,len * sizeof(T));
}
}
template
<typename T>
void printArray(T infernalArrayPrintable[],int len)
{
for(int i=0;i<len;i++)
{
std::cout << infernalArrayPrintable[i] << " ";
}
std::cout << std::endl;
}
template
<>
void printArray(VeryElaboratedDataType infernalArrayPrintable[],int len)
{
for(int i=0;i<len;i++)
{
std::cout << infernalArrayPrintable[i].a << "," << infernalArrayPrintable[i].b << " ";
}
std::cout << std::endl;
}
}
}
int main() {
// your code goes here
int myInfernalArray[] = {1,2,3,4,5,6,7,8,9};
VeryElaboratedDataType myInfernalArrayV[] = {{1,1},{2,2},{3,3},{4,4},{5,5},{6,6},{7,7},{8,8},{9,9}};
amsoft::inutils::printArray(myInfernalArray,sizeof(myInfernalArray)/sizeof(int));
amsoft::inutils::infernalShift<int,sizeof(myInfernalArray)/sizeof(int)>(myInfernalArray,4);
amsoft::inutils::printArray(myInfernalArray,sizeof(myInfernalArray)/sizeof(int));
amsoft::inutils::infernalShift<int,sizeof(myInfernalArray)/sizeof(int)>(myInfernalArray,4,amsoft::inutils::EShiftDirection::Left);
amsoft::inutils::printArray(myInfernalArray,sizeof(myInfernalArray)/sizeof(int));
amsoft::inutils::infernalShift<int,sizeof(myInfernalArray)/sizeof(int)>(myInfernalArray,10);
amsoft::inutils::printArray(myInfernalArray,sizeof(myInfernalArray)/sizeof(int));
amsoft::inutils::printArray(myInfernalArrayV,sizeof(myInfernalArrayV)/sizeof(VeryElaboratedDataType));
amsoft::inutils::infernalShift<VeryElaboratedDataType,sizeof(myInfernalArrayV)/sizeof(VeryElaboratedDataType)>(myInfernalArrayV,4);
amsoft::inutils::printArray(myInfernalArrayV,sizeof(myInfernalArrayV)/sizeof(VeryElaboratedDataType));
amsoft::inutils::infernalShift<VeryElaboratedDataType,sizeof(myInfernalArrayV)/sizeof(VeryElaboratedDataType)>(myInfernalArrayV,4,amsoft::inutils::EShiftDirection::Left);
amsoft::inutils::printArray(myInfernalArrayV,sizeof(myInfernalArrayV)/sizeof(VeryElaboratedDataType));
amsoft::inutils::infernalShift<VeryElaboratedDataType,sizeof(myInfernalArrayV)/sizeof(VeryElaboratedDataType)>(myInfernalArrayV,10);
amsoft::inutils::printArray(myInfernalArrayV,sizeof(myInfernalArrayV)/sizeof(VeryElaboratedDataType));
return 0;
}
Похож на @IsaacTurner и не очень элегантен из-за ненужного копирования, но реализация довольно короткая.
Идея - поменять элемент A на индекс 0 с элементом B, который находится в пункте назначения A. Теперь B - первый. Поменяйте его с элементом C, который находится в пункте назначения B. Продолжайте, пока пункт назначения не будет в 0.
Если наибольший общий делитель не равен 1, значит, вы еще не закончили - вам нужно продолжить замену, но теперь используйте индекс 1 в начальной и конечной точке.
Продолжайте, пока ваша стартовая позиция не будет gcd.
int gcd(int a, int b) => b == 0 ? a : gcd(b, a % b);
public int[] solution(int[] A, int K)
{
for (var i = 0; i < gcd(A.Length, K); i++)
{
for (var j = i; j < A.Length - 1; j++)
{
var destIndex = ((j-i) * K + K + i) % A.Length;
if (destIndex == i) break;
var destValue = A[destIndex];
A[destIndex] = A[i];
A[i] = destValue;
}
}
return A;
}
В зависимости от используемой структуры данных, вы можете сделать это в O(1). Я думаю, что самый быстрый способ - это держать массив в форме связанного списка и иметь хеш-таблицу, которая может переводить между "индексом" в массиве и "указателем" на запись. Таким образом, вы можете найти соответствующие головы и хвосты в O (1) и выполнить переподключение в O (1) (и обновить хэш-таблицу после переключения в O (1)). Это, конечно, было бы очень "грязным" решением, но если все, что вас интересует, это скорость сдвига, которая будет делать (за счет более длинной вставки и поиска в массиве, но она все равно останется O (1))
Если у вас есть данные в чистом массиве, я не думаю, что вы можете избежать O (n).
Кодирование зависит от того, какой язык вы используете.
В Python, например, вы можете "нарезать" его (предположим, что n - это размер смещения):
result = original[-n:]+original[:-n]
(Я знаю, что поиск хеша в теории не O (1), но мы здесь практичны, а не теоретичны, по крайней мере, я на это надеюсь...)
circleArray имеет некоторые ошибки и работает не во всех случаях!
Цикл должен продолжаться while i1 < i2 НЕ i1 < last - 1,
void Shift(int* _array, int _size, int _moves)
{
_moves = _size - _moves;
int i2 = _moves;
int i1 = -1;
while(++i1 < i2)
{
int tmp = _array[i2];
_array[i2] = _array[i1];
_array[i1] = tmp;
if(++i2 == _size) i2 = _moves;
}
}
Вот еще один (C++):
void shift_vec(vector<int>& v, size_t a)
{
size_t max_s = v.size() / a;
for( size_t s = 1; s < max_s; ++s )
for( size_t i = 0; i < a; ++i )
swap( v[i], v[s*a+i] );
for( size_t i = 0; i < a; ++i )
swap( v[i], v[(max_s*a+i) % v.size()] );
}
Конечно, это не так элегантно, как знаменитое решение "трижды в обратном направлении", но в зависимости от машины оно может быть примерно таким же быстрым.
Сохраните два индекса в массиве, один индекс начинается от начала массива до конца массива. Другой индекс начинается с M-й позиции с последнего и проходит по последним M-элементам любое количество раз. Принимает O(n) во все времена. Не требуется дополнительного места.
circleArray(Elements,M){
int size=size-of(Elements);
//first index
int i1=0;
assert(size>M)
//second index starting from mth position from the last
int i2=size-M;
//until first index reaches the end
while(i1<size-1){
//swap the elements of the array pointed by both indexes
swap(i1,i2,Elements);
//increment first pointer by 1
i1++;
//increment second pointer. if it goes out of array, come back to
//mth position from the last
if(++i2==size) i2=size-M;
}
}