Java рекурсивный треугольник с отклонением

Question

Здравствуйте, я довольно новичок в программировании, и я пытаюсь, в Java, создать функцию, которая создает рекурсивные треугольники из больших точек треугольников между углами, где новые точки треугольников отклоняются от нормального положения в y-значении. Смотрите фотографии ниже для визуализации.

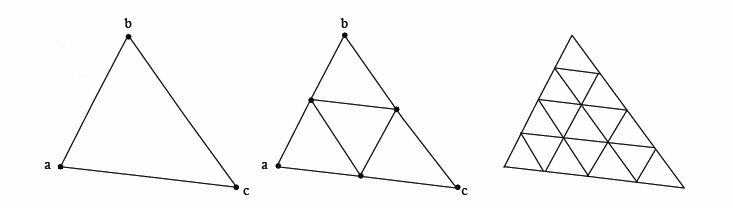
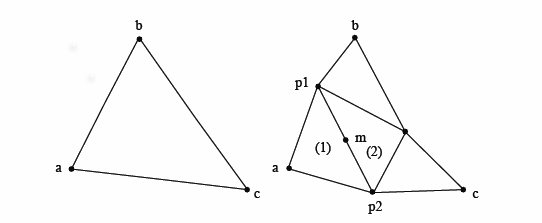
На первом рисунке показана прогрессия рекурсивного алгоритма без каких-либо отклонений (порядок 0,1,2), а на втором рисунке - с (порядок 0,1).

Мне удалось создать работающий кусок кода, который создает именно то, что я хочу для первых двух ордеров, но когда мы достигаем порядка 2 и выше, я сталкиваюсь с проблемой, когда меньшие треугольники не используют одни и те же средние точки и поэтому выглядят как картинка ниже.

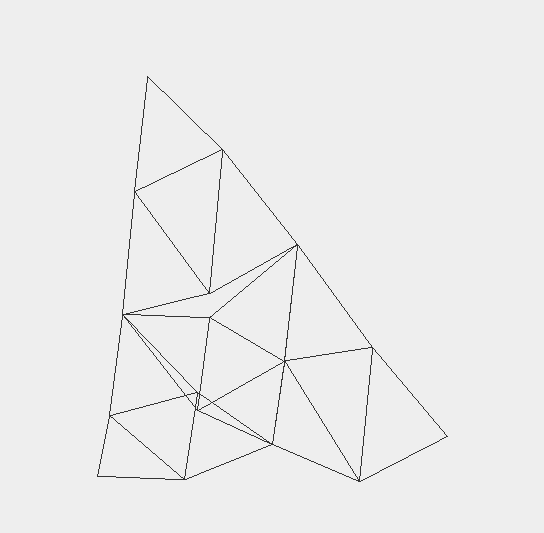
Поэтому мне нужна помощь с тем, чтобы хранить и называть правильные средние точки для каждого из треугольников. Я думал о реализации нового класса, который контролирует вычисление средних точек и сохраняет их и т. Д., Но, как я уже сказал, мне нужна помощь в этом.

Ниже мой текущий код

Класс point хранит значения a x и y для точки

lineBetween создает линию между выбранными точками

void fractalLine(TurtleGraphics turtle, int order, Point ett, Point tva, Point tre, int dev) {


    if(order == 0){
        lineBetween(ett,tva,turtle);
        lineBetween(tva,tre,turtle);
        lineBetween(tre,ett,turtle);
    } else {

            double deltaX = tva.getX() - ett.getX();
            double deltaY = tva.getY() - ett.getY();

            double deltaXtre = tre.getX() - ett.getX();
            double deltaYtre = tre.getY() - ett.getY();

            double deltaXtva = tva.getX() - tre.getX();
            double deltaYtva = tva.getY() - tre.getY();

            Point one;
            Point two;
            Point three;

            double xt = ((deltaX/2))+ett.getX();
            double yt = ((deltaY/2))+ett.getY() +RandomUtilities.randFunc(dev);
            one = new Point(xt,yt);

            xt = (deltaXtre/2)+ett.getX();
            yt = (deltaYtre/2)+ett.getY() +RandomUtilities.randFunc(dev);
            two = new Point(xt,yt);

            xt = ((deltaXtva/2))+tre.getX();
            yt = ((deltaYtva/2))+tre.getY() +RandomUtilities.randFunc(dev);
            three = new Point(xt,yt);

            fractalLine(turtle,order-1,one,tva,three,dev/2);
            fractalLine(turtle,order-1,ett,one,two,dev/2);
            fractalLine(turtle,order-1,two,three,tre,dev/2);
            fractalLine(turtle,order-1,one,two,three,dev/2);            
    }
}

Заранее спасибо

Виктор

Answer 1

Вы можете определить треугольник по 3 точкам (вершинам). Таким образом, вершины a, b и c образуют треугольник. Комбинации ab, ac и bc будут ребрами. Итак, алгоритм идет:

1. Сначала начните с трех вершин a, b и c
2. Получите средние точки 3 ребер p1,p2 и p3 и получите 4 набора вершин для 4 меньших треугольников. т.е. (a,p1,p2),(b,p1,p3),(c,p2,p3) и (p1,p2,p3)
3. Рекурсивно найдите подтреугольники 4 треугольников, пока глубина не будет достигнута.

Таким образом, как грубое руководство, код идет

findTriangles(Vertexes[] triangle, int currentDepth) {
    //Depth is reached.
    if(currentDepth == depth) {
          store(triangle);
          return;
    }
    Vertexes[] first = getFirstTriangle(triangle); 
    Vertexes[] second = getSecondTriangle(triangle);
    Vertexes[] third = getThirdTriangle(triangle);;
    Vertexes[] fourth = getFourthTriangle(triangle)

    findTriangles(first, currentDepth+1);  
    findTriangles(second, currentDepth+1);
    findTriangles(third, currentDepth+1);
    findTriangles(fourth, currentDepth+1);
}     

Вы должны хранить соответствующие треугольники в структуре данных.

Answer 2

Вы вычисляете средние точки любой вершины снова и снова на разных путях вашей рекурсии. Пока вы не меняете их случайным образом, вы получаете одинаковую среднюю точку для каждого пути, поэтому проблем нет. Но, конечно, если вы измените средние точки случайным образом, вы получите две разные средние точки на двух разных путях рекурсии.

Вы можете изменить свой алгоритм так, чтобы вы не только проходили вдоль 3 углов треугольника, но и изменяли средние точки каждой вершины. Или вы храните их в отдельном списке или на карте, или что-то в этом роде, и вычисляете их только один раз, а в противном случае ищите их.