"расшифровать" приближение греха Тейлора
Я использую ряд Тейлора для вычисления sin(), Ряд Тейлора для греха:
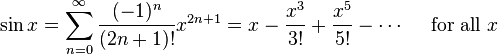
Реализация, которую я использую, выглядит следующим образом:
float sine(float x, int j)
{
float val = 1;
for (int k = j - 1; k >= 0; --k)
val = 1 - x*x/(2*k+2)/(2*k+3)*val;
return x * val;
}
Насколько я понимаю, этот код является приблизительным j члены полинома (Другими словами, аппроксимация является сумматором от нуля до j вместо от нуля до ∞), k является n в формуле, и, конечно, x является x,
Я пытаюсь понять эту реализацию, то есть преобразование из приведенной выше формулы в код. Моя цель - написать такую же реализацию для cos() серии.
Не могли бы вы помочь мне понять это? Спасибо
1 ответ
Это серия Маклаурина, но она написана так, чтобы уменьшить количество вычислений, использующих формулу повторения для общего члена ряда.
Версия для косинуса следующая (вместе с простым тестовым набором):
#include <stdio.h>
#include <math.h>
float cosine(float x, int j)
{
float val = 1;
for (int k = j - 1; k >= 0; --k)
val = 1 - x*x/(2*k+2)/(2*k+1)*val;
return val;
}
int main( void )
{
for( double x = 0.0; x <= 1.57; x += 0.1 )
{
printf("%10g %10g %10g\n", x, cos(x), cosine(x, 5));
}
return 0;
}
РЕДАКТИРОВАТЬ (заменил уродливую текстовую математику на изображения, созданные с помощью LaTeX)
Чтобы понять трюк, давайте сосредоточимся на sine Пример и напомним расширение Маклаурина функции синуса:

Теперь давайте выполним разложение до 5-го члена (N=5), пренебрегаем остатком R и выполним некоторое переписывание с использованием факторизаций x2 членов. Получающиеся шаги описаны ниже, где переписанные подвыражения отмечены числом в квадратных скобках:
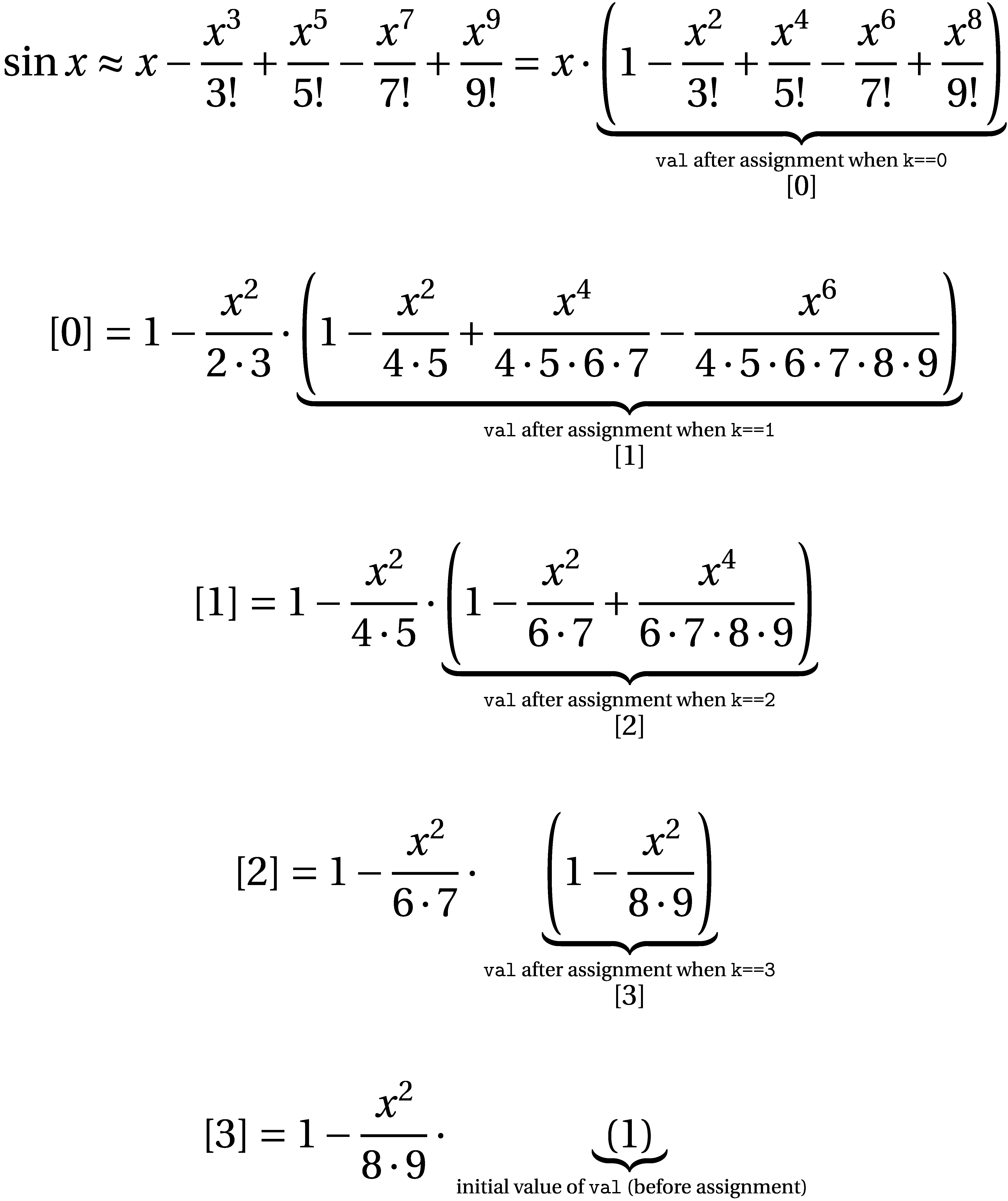
Функция C - это просто реализация этой рекурсивной перезаписи снизу вверх, то есть то, что выглядит как последний шаг в приведенной выше схеме, вычисляется первым в sine функция (пример относится к вызову с j==4, так что переменная цикла k начинается со значения 3 и спускается к 0)