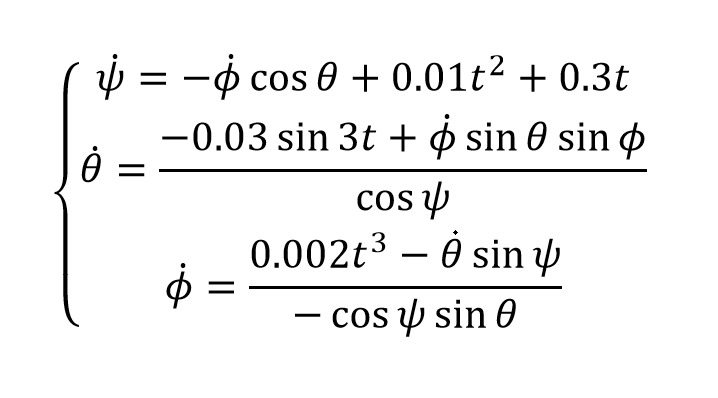Решить связанную ОДУ эйлеровых ангелов Вектор вращения тела

Question

Я пытаюсь решить связанные ODE с помощью функции Matlab Ode45:

Вот моя функция под названием 'Rot', чтобы описать эти ODE для использования matlab ode45.

function omega= Rot(t,y)
omega(2,1)=(0.03*sin(3*t)*((cos(Y(1)))^2)+0.002*t^3*sin(y(1)))...
/-((cos(Y(1)))^2)+((sin(Y(1)))^2);
omega(1,1)=((0.002*t^2-omega(2,1)*sin(y(1)))...
/-cos(y(3))*sin(y(2)))*cos(y(2))+0.01*t^2+0.3*t;
omega(3,1)=(0.002*t^2-omega(2,1)*sin(y(1)))...
/-cos(y(3))*sin(y(2));

но я получаю "Недостаточно входных аргументов". ошибка.

Answer 1

Хорошо, так выражая theta_dot как функция других переменных в уравнении (3) и введя результат в уравнение (2), я получаю (псевдокод):

phi_dot = (0.03*sin(psi)*sin(3*t) - 0.002*t^2 * cos(psi)) / (sin(theta)*(cos(psi))^2 + sin(theta) * sin(psi) * sin(phi))

Так получается, что первое уравнение вашего ODE-файла зависит только от времени и вектора состояния.

Тогда ваше второе уравнение в файле ODE:

psi_dot = -phi_dot * cos(theta) + 0.01*t^2 + 0.3*t

это нормально, потому что вы рассчитали phi_dot в предыдущем уравнении.

И, наконец, последнее уравнение в вашем файле ODE:

theta_dot = (-0.03*sin(3*t) + phi_dot * sin(theta) * sin(phi)) / cos(psi);

что тоже нормально, потому что вы рассчитали phi_dot в вашем первом уравнении.

Затем вы можете передать это в ODE Solver, и он должен работать. (проверить мои математику, хотя)