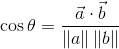Получить вращение XYZ от PVector

Question

У меня нормализовался PVector это представляет направление от происхождения:

PVector dir = new PVector(-0.1, 0.8, 0.3);

Я хотел бы получить углы X, Y и Z в этом направлении, чтобы я мог использовать rotateX()и т. д. матричные преобразования.

В 2D я бы использовал atan2() чтобы получить угол, но я понятия не имею, как сделать это для 3D-точки.

Answer 1

Я нахожу угол с осями с помощью точечного произведения. Все мои векторы называются GravVectorВ основном потому, что я использую его в гравитационных симуляциях n-тела. Моя реализация вектора имеет такие методы, как .magnitude() легко вернуть величину вектора, то, что вам нужно.

Точечное произведение в основном умножается на значения вектора X, Y и Z, а затем суммирует все эти произведения. Для трех измерений это можно записать явно так:

public double dotProduct(GravVector vector) {
    return this.x * vector.x + this.y * vector.y + this.z * vector.z;
}

Теперь, у точечного произведения есть хорошая характеристика, где произведение эквивалентно амплитудам двух векторов, умноженным на косинус угла между этими двумя векторами. Это, когда смещено вокруг, становится этим:

Это означает, что для нахождения угла вы можете просто арккосинить значение правой стороны.

Мой код делает это ниже, получая doubleс angleX, angleY, а также angleZ, Обратите внимание, что результат в радианах. Если вы хотите это в градусах, вам нужно умножить все, что у вас есть в радианах, на 180 / Math.PI,

GravVector vector = new GravVector(1, 1, 0);

// magnitude * 1 because the magnitude of the temporary vector is 1.
double angleX = Math.acos(vector.dotProduct(new GravVector(1, 0, 0)) / (vector.magnitude() * 1));
double angleY = Math.acos(vector.dotProduct(new GravVector(0, 1, 0)) / (vector.magnitude() * 1));
double angleZ = Math.acos(vector.dotProduct(new GravVector(0, 0, 1)) / (vector.magnitude() * 1));

// in radians
System.out.println(String.format("x: %.2f, y: %.2f, z: %.2f",
        angleX, angleY, angleZ));

// in degrees
System.out.println(String.format("x: %.2f, y: %.2f, z: %.2f",
        angleX * 180 / Math.PI,
        angleY * 180 / Math.PI, 
        angleZ * 180 / Math.PI));

Вывод на консоль, который выводится на печать: первая строка в радианах, вторая строка в градусах:

x: 0.79, y: 0.79, z: 1.57
x: 45.00, y: 45.00, z: 90.00

Вы можете легко обобщить это, чтобы получить угол между любыми двумя векторами (не имеет значения, имеют ли они единичную величину или нет) следующим образом:

public static double angleBetween(GravVector v1, GravVector v2) {
    return Math.acos(v1.dotProduct(v2) / (v1.magnitude() * v2.magnitude())); 
    // in radians
}

---

РЕДАКТИРОВАТЬ. Учтите, что по отношению к любой из осей скалярное произведение всегда будет эквивалентно соответствующему компоненту. Таким образом, для оси X это будет просто компонент X.

Это означает, что вы можете упростить вычисления и использовать такие методы:

public static double xAngle(GravVector vector) {
    return Math.acos(vector.x / (vector.magnitude()));
}

public static double yAngle(GravVector vector) {
    return Math.acos(vector.y / (vector.magnitude()));
}

public static double zAngle(GravVector vector) {
    return Math.acos(vector.z / (vector.magnitude()));
}

Для примера вектора с компонентами [1, 1, 0], если вы вызвали и напечатали значения для каждого из этих методов, это приведет к следующему, что согласуется с вышеуказанными значениями:

x, rad: 0.7853981633974484
y, rad: 0.7853981633974484
z, rad: 1.5707963267948966

Answer 2

Не уверен на 100%, понял ли я, что вы имеете в виду под углами x, y, z, но я думаю, что в случае "угла z", чтобы использовать ваши слова, угол, необходимый для поворота вектора с началом координат (0, 0, 0) и заканчиваются, где Z равно 0, и он идет вдоль оси X или Y (это будет ваш выбор), чтобы повернуть его вокруг оси Z так, чтобы результирующий вектор был проекцией исходного вектора на плоскость X,Y, проекция которой попросту (x, y, 0).

Этот угол вокруг Z был бы арктангенсом y/x или (x/y).

Сделайте то же самое для оси X и оси Y, и у вас есть эти три угла поворота. Вам нужно только два из них и начальный вектор, но я не знаю, имеет ли это отношение к проблеме.