Нахождение формы и масштаба гамма-распределения с учетом домашнего диапазона

Question

Ниже вставлен дополнительный материал из статьи. После нахождения значений домашнего диапазона авторы говорят: "Гамма (13,10) прекрасно это охватывает". Как авторы нашли 13 и 10?

# Moldenhauer and Regelski (1996) state that home range size typically
# ranges from 0.08-0.65 ha, which equates to a radius of
sqrt(0.08/pi*10000) # 15.96 m or
sqrt(0.65/pi*10000) # 45.49 m

# Since parulas were detected by song, let's be safe
# and add a minimum and maximum
# distance at which they could be heard, 50 and 250 m, based upon
# Simons et al. (2009).
# So now we have an area between
(15.96+50)^2*pi / 10000  # 1.37 ha, and
(45.49+250)^2*pi / 10000 # 27.4 ha

# We note that this is a very large range.

# Following Royle et. al (2011), and assuming a
# chi-squared distribution with 2 degrees of freedom,
# the range of sigma is given by
sqrt(1.37*10000/pi)/sqrt(5.99)   # 27 m
sqrt(27.4*10000/pi)/sqrt(5.99)   # 120 m

# In our grid spacing, 1 unit = 50m, so our we want a prior with most
# of the density between:
27/50  # 0.54
121/50 # 2.42

# Gamma(13, 10) covers this nicely
qgamma(c(0.001, 0.5, 0.999), 13, 10)

plot(function(x) dgamma(x, 13, 10), 0, 5, xlim=c(0, 3), ylim=c(0, 1.5))**

Answer 1

Честно говоря, я думаю, что ответом на это может быть просто махание рукой. Если бы я выбрал гамма-предшественник и имел некоторую интуицию в отношении диапазона, я бы нашел медианное значение и сделал бы его средним значением гамма-распределения. Так что для этого примера я бы сделал что-то вроде:

# Find median of range (which is 1.48)
gamma_med <- median(seq(0.54, 2.42, length.out = 1e6))

Распределение гаммы имеет два параметра, гамма (а, б). Первый момент, или среднее значение, можно легко вычислить, потому что это просто a/b, Поэтому, если мы хотим, чтобы наше среднее значение было 1,48, нам просто нужно выбрать форму (а) и масштаб (b), отношение которых равно 1,48. Самый простой будет gamma(14.8, 10), но мы могли бы увеличить или уменьшить нашу дисперсию, изменив эти параметры (дисперсия гамма = a/(b^2)).

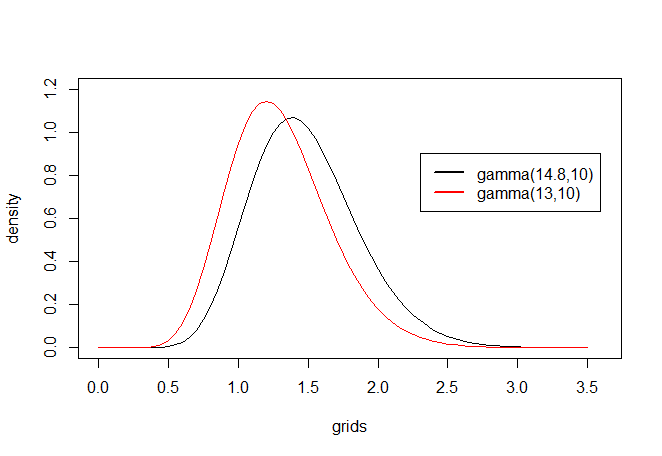
Вот как отличаются эти два приората, вы можете увидеть, как гамма (13,10) является более точной. В конце концов, в действительности все сводится к тому, что вы считаете оправданным в том, каким вы хотите, чтобы ваши приоры были (или, предпочтительно, вы должны использовать несколько приоров, чтобы увидеть, как они влияют на ваш зад).