Самый быстрый способ сортировки 10 номеров? (числа 32 битные)
Я решаю проблему, и она включает в себя сортировку 10 чисел (int32) очень быстро. Мое приложение должно сортировать 10 чисел в миллионы раз как можно быстрее. Я выбираю набор данных из миллиардов элементов, и каждый раз мне нужно выбрать из него 10 чисел (упрощенно) и отсортировать их (и сделать выводы из отсортированного списка из 10 элементов).
В настоящее время я использую сортировку вставками, но я представляю, что мог бы реализовать очень быстрый пользовательский алгоритм сортировки для моей конкретной задачи из 10 чисел, который превзошел бы сортировку вставками.
У кого-нибудь есть идеи о том, как подойти к этой проблеме?
12 ответов
(Вслед за предложением HelloWorld изучить сети сортировки.)
Кажется, что сеть из 29 сравнений / свопов - это самый быстрый способ сделать сортировку с 10 входами. Я использовал сеть, обнаруженную Ваксманом в 1969 году для этого примера в Javascript, который должен быть переведен непосредственно в C, так как это просто список if заявления, сравнения и свопы.
function sortNet10(data) { // ten-input sorting network by Waksman, 1969
var swap;
if (data[0] > data[5]) { swap = data[0]; data[0] = data[5]; data[5] = swap; }
if (data[1] > data[6]) { swap = data[1]; data[1] = data[6]; data[6] = swap; }
if (data[2] > data[7]) { swap = data[2]; data[2] = data[7]; data[7] = swap; }
if (data[3] > data[8]) { swap = data[3]; data[3] = data[8]; data[8] = swap; }
if (data[4] > data[9]) { swap = data[4]; data[4] = data[9]; data[9] = swap; }
if (data[0] > data[3]) { swap = data[0]; data[0] = data[3]; data[3] = swap; }
if (data[5] > data[8]) { swap = data[5]; data[5] = data[8]; data[8] = swap; }
if (data[1] > data[4]) { swap = data[1]; data[1] = data[4]; data[4] = swap; }
if (data[6] > data[9]) { swap = data[6]; data[6] = data[9]; data[9] = swap; }
if (data[0] > data[2]) { swap = data[0]; data[0] = data[2]; data[2] = swap; }
if (data[3] > data[6]) { swap = data[3]; data[3] = data[6]; data[6] = swap; }
if (data[7] > data[9]) { swap = data[7]; data[7] = data[9]; data[9] = swap; }
if (data[0] > data[1]) { swap = data[0]; data[0] = data[1]; data[1] = swap; }
if (data[2] > data[4]) { swap = data[2]; data[2] = data[4]; data[4] = swap; }
if (data[5] > data[7]) { swap = data[5]; data[5] = data[7]; data[7] = swap; }
if (data[8] > data[9]) { swap = data[8]; data[8] = data[9]; data[9] = swap; }
if (data[1] > data[2]) { swap = data[1]; data[1] = data[2]; data[2] = swap; }
if (data[3] > data[5]) { swap = data[3]; data[3] = data[5]; data[5] = swap; }
if (data[4] > data[6]) { swap = data[4]; data[4] = data[6]; data[6] = swap; }
if (data[7] > data[8]) { swap = data[7]; data[7] = data[8]; data[8] = swap; }
if (data[1] > data[3]) { swap = data[1]; data[1] = data[3]; data[3] = swap; }
if (data[4] > data[7]) { swap = data[4]; data[4] = data[7]; data[7] = swap; }
if (data[2] > data[5]) { swap = data[2]; data[2] = data[5]; data[5] = swap; }
if (data[6] > data[8]) { swap = data[6]; data[6] = data[8]; data[8] = swap; }
if (data[2] > data[3]) { swap = data[2]; data[2] = data[3]; data[3] = swap; }
if (data[4] > data[5]) { swap = data[4]; data[4] = data[5]; data[5] = swap; }
if (data[6] > data[7]) { swap = data[6]; data[6] = data[7]; data[7] = swap; }
if (data[3] > data[4]) { swap = data[3]; data[3] = data[4]; data[4] = swap; }
if (data[5] > data[6]) { swap = data[5]; data[5] = data[6]; data[6] = swap; }
return(data);
}
alert(sortNet10([5,7,1,8,4,3,6,9,2,0]));Вот графическое представление сети, разделенной на независимые фазы.
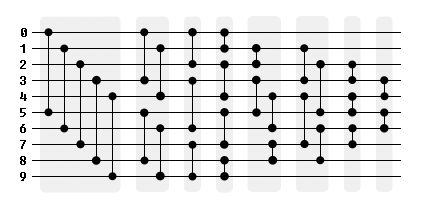
Чтобы воспользоваться преимуществами параллельной обработки, группировка 5-4-3-4-4-4-3-2 может быть преобразована в группировку 4-4-4-4-4-4-3-2.
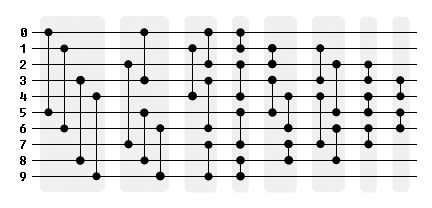
Когда вы работаете с этим фиксированным размером, обратите внимание на Сортировку сетей. Эти алгоритмы имеют фиксированное время выполнения и не зависят от их ввода. Для вашего варианта использования у вас нет таких накладных расходов, как у некоторых алгоритмов сортировки.
Битонная сортировка - это реализация такой сети. Этот лучше всего работает с len(n) <= 32 на процессоре. На больших входах вы можете подумать о переходе на графический процессор. https://en.wikipedia.org/wiki/Sorting_network
Кстати, здесь есть хорошая страница для сравнения алгоритмов сортировки (хотя в ней отсутствует bitonic sort,
Используйте сортировочную сеть, у которой есть сравнения в группах по 4, так что вы можете сделать это в SIMD-регистрах. Пара упакованных инструкций min/max реализует упакованную функцию компаратора. Извините, у меня нет времени сейчас искать страницу, которую я помню об этом, но, надеюсь, поиск в сетях сортировки SIMD или SSE что-то даст.
x86 SSE имеет упакованные 32-битные целочисленные инструкции min и max для векторов четырех 32-битных целых. AVX2 (Haswell и более поздние версии) имеют то же самое, но для векторов 256b по 8 дюймов. Есть также эффективные инструкции по перемешиванию.
Если у вас много независимых небольших сортировок, может быть возможно выполнить 4 или 8 сортировок параллельно, используя векторы. Особенно если вы выбираете элементы случайным образом (так что сортируемые данные в любом случае не будут непрерывными в памяти), вы можете избежать перемешивания и просто сравнивать их в нужном вам порядке. 10 регистров для хранения всех данных из 4 (AVX2: 8) списков по 10 дюймов по-прежнему оставляют 6 регистров на пустом месте.
Сети векторной сортировки менее эффективны, если вам также необходимо отсортировать связанные данные. В этом случае наиболее эффективным способом, по-видимому, является использование упакованного сравнения для получения маски, элементы которой были изменены, и использование этой маски для смешивания векторов (ссылок на) связанных данных.
А как насчет развернутой сортировки без веток?
#include <iostream>
#include <algorithm>
#include <random>
//return the index of the minimum element in array a
int min(const int * const a) {
int m = a[0];
int indx = 0;
#define TEST(i) (m > a[i]) && (m = a[i], indx = i );
//see http://stackru.com/a/7074042/2140449
TEST(1);
TEST(2);
TEST(3);
TEST(4);
TEST(5);
TEST(6);
TEST(7);
TEST(8);
TEST(9);
#undef TEST
return indx;
}
void sort( int * const a ){
int work[10];
int indx;
#define GET(i) indx = min(a); work[i] = a[indx]; a[indx] = 2147483647;
//get the minimum, copy it to work and set it at max_int in a
GET(0);
GET(1);
GET(2);
GET(3);
GET(4);
GET(5);
GET(6);
GET(7);
GET(8);
GET(9);
#undef GET
#define COPY(i) a[i] = work[i];
//copy back to a
COPY(0);
COPY(1);
COPY(2);
COPY(3);
COPY(4);
COPY(5);
COPY(6);
COPY(7);
COPY(8);
COPY(9);
#undef COPY
}
int main() {
//generating and printing a random array
int a[10] = { 1,2,3,4,5,6,7,8,9,10 };
std::random_device rd;
std::mt19937 g(rd());
std::shuffle( a, a+10, g);
for (int i = 0; i < 10; i++) {
std::cout << a[i] << ' ';
}
std::cout << std::endl;
//sorting and printing again
sort(a);
for (int i = 0; i < 10; i++) {
std::cout << a[i] << ' ';
}
return 0;
}
/questions/15664839/kakoj-samyij-byistryij-sposob-poluchit-znachenie/15664843#15664843
Единственные соответствующие строки - первые два #define,
Он использует два списка и полностью перепроверяет первый из них десять раз, что было бы плохо реализованной сортировкой выбора, однако он избегает ветвей и циклов переменной длины, которые могут компенсировать это современными процессорами и таким небольшим набором данных.
эталонный тест
Я сравнил сеть сортировки, и мой код выглядит медленнее. Однако я попытался удалить развертывание и копию. Запуск этого кода:
#include <iostream>
#include <algorithm>
#include <random>
#include <chrono>
int min(const int * const a, int i) {
int m = a[i];
int indx = i++;
for ( ; i<10; i++)
//see http://stackru.com/a/7074042/2140449
(m > a[i]) && (m = a[i], indx = i );
return indx;
}
void sort( int * const a ){
for (int i = 0; i<9; i++)
std::swap(a[i], a[min(a,i)]); //search only forward
}
void sortNet10(int * const data) { // ten-input sorting network by Waksman, 1969
int swap;
if (data[0] > data[5]) { swap = data[0]; data[0] = data[5]; data[5] = swap; }
if (data[1] > data[6]) { swap = data[1]; data[1] = data[6]; data[6] = swap; }
if (data[2] > data[7]) { swap = data[2]; data[2] = data[7]; data[7] = swap; }
if (data[3] > data[8]) { swap = data[3]; data[3] = data[8]; data[8] = swap; }
if (data[4] > data[9]) { swap = data[4]; data[4] = data[9]; data[9] = swap; }
if (data[0] > data[3]) { swap = data[0]; data[0] = data[3]; data[3] = swap; }
if (data[5] > data[8]) { swap = data[5]; data[5] = data[8]; data[8] = swap; }
if (data[1] > data[4]) { swap = data[1]; data[1] = data[4]; data[4] = swap; }
if (data[6] > data[9]) { swap = data[6]; data[6] = data[9]; data[9] = swap; }
if (data[0] > data[2]) { swap = data[0]; data[0] = data[2]; data[2] = swap; }
if (data[3] > data[6]) { swap = data[3]; data[3] = data[6]; data[6] = swap; }
if (data[7] > data[9]) { swap = data[7]; data[7] = data[9]; data[9] = swap; }
if (data[0] > data[1]) { swap = data[0]; data[0] = data[1]; data[1] = swap; }
if (data[2] > data[4]) { swap = data[2]; data[2] = data[4]; data[4] = swap; }
if (data[5] > data[7]) { swap = data[5]; data[5] = data[7]; data[7] = swap; }
if (data[8] > data[9]) { swap = data[8]; data[8] = data[9]; data[9] = swap; }
if (data[1] > data[2]) { swap = data[1]; data[1] = data[2]; data[2] = swap; }
if (data[3] > data[5]) { swap = data[3]; data[3] = data[5]; data[5] = swap; }
if (data[4] > data[6]) { swap = data[4]; data[4] = data[6]; data[6] = swap; }
if (data[7] > data[8]) { swap = data[7]; data[7] = data[8]; data[8] = swap; }
if (data[1] > data[3]) { swap = data[1]; data[1] = data[3]; data[3] = swap; }
if (data[4] > data[7]) { swap = data[4]; data[4] = data[7]; data[7] = swap; }
if (data[2] > data[5]) { swap = data[2]; data[2] = data[5]; data[5] = swap; }
if (data[6] > data[8]) { swap = data[6]; data[6] = data[8]; data[8] = swap; }
if (data[2] > data[3]) { swap = data[2]; data[2] = data[3]; data[3] = swap; }
if (data[4] > data[5]) { swap = data[4]; data[4] = data[5]; data[5] = swap; }
if (data[6] > data[7]) { swap = data[6]; data[6] = data[7]; data[7] = swap; }
if (data[3] > data[4]) { swap = data[3]; data[3] = data[4]; data[4] = swap; }
if (data[5] > data[6]) { swap = data[5]; data[5] = data[6]; data[6] = swap; }
}
std::chrono::duration<double> benchmark( void(*func)(int * const), const int seed ) {
std::mt19937 g(seed);
int a[10] = {10,11,12,13,14,15,16,17,18,19};
std::chrono::high_resolution_clock::time_point t1, t2;
t1 = std::chrono::high_resolution_clock::now();
for (long i = 0; i < 1e7; i++) {
std::shuffle( a, a+10, g);
func(a);
}
t2 = std::chrono::high_resolution_clock::now();
return std::chrono::duration_cast<std::chrono::duration<double>>(t2 - t1);
}
int main() {
std::random_device rd;
for (int i = 0; i < 10; i++) {
const int seed = rd();
std::cout << "seed = " << seed << std::endl;
std::cout << "sortNet10: " << benchmark(sortNet10, seed).count() << std::endl;
std::cout << "sort: " << benchmark(sort, seed).count() << std::endl;
}
return 0;
}
Я последовательно получаю лучший результат для сортировки без ветвления по сравнению с сетью сортировки.
$ gcc -v
gcc version 5.2.0 (GCC)
$ g++ -std=c++11 -Ofast sort.cpp && ./a.out
seed = -1727396418
sortNet10: 2.24137
sort: 2.21828
seed = 2003959850
sortNet10: 2.23914
sort: 2.21641
seed = 1994540383
sortNet10: 2.23782
sort: 2.21778
seed = 1258259982
sortNet10: 2.25199
sort: 2.21801
seed = 1821086932
sortNet10: 2.25535
sort: 2.2173
seed = 412262735
sortNet10: 2.24489
sort: 2.21776
seed = 1059795817
sortNet10: 2.29226
sort: 2.21777
seed = -188551272
sortNet10: 2.23803
sort: 2.22996
seed = 1043757247
sortNet10: 2.2503
sort: 2.23604
seed = -268332483
sortNet10: 2.24455
sort: 2.24304
Вопрос не говорит о том, что это какое-то веб-приложение. Единственное, что бросилось в глаза, было:
Я выбираю набор данных из миллиардов элементов, и каждый раз мне нужно выбрать из него 10 чисел (упрощенно) и отсортировать их (и сделать выводы из отсортированного списка из 10 элементов).
Как инженер по программному и аппаратному обеспечению это абсолютно кричит "FPGA" для меня. Я не знаю, какие выводы вы должны сделать из отсортированного набора чисел или откуда поступают данные, но я знаю, что было бы почти тривиально обрабатывать где-то от ста миллионов до миллиарда этих "сортировать и анализировать "операций в секунду. В прошлом я занимался секвенированием ДНК с помощью FPGA. Практически невозможно превзойти огромную вычислительную мощность ПЛИС, если проблема хорошо подходит для решения такого типа.
На каком-то уровне единственным ограничивающим фактором становится то, как быстро вы можете поместить данные в FPGA и как быстро вы можете получить их.
Для справки я разработал высокопроизводительный процессор обработки изображений в реальном времени, который получал 32-битные данные RGB-изображения со скоростью около 300 миллионов пикселей в секунду. Данные передаются на другой конец через фильтры КИХ, умножители матриц, таблицы поиска, блоки обнаружения краев пространства и ряд других операций. Все это на относительно небольшой FPGA Xilinx Virtex2 с тактовой частотой от 33 МГц до, если я правильно помню, 400 МГц. О, да, он также имел реализацию контроллера DDR2 и управлял двумя банками памяти DDR2.
ПЛИС может выводить своего рода десять 32-битных чисел на каждом тактовом переходе, работая на сотнях МГц. В начале операции будет небольшая задержка, поскольку данные заполняют конвейер обработки данных. После этого вы сможете получить один результат за такт. Или больше, если обработка может быть распараллелена посредством репликации конвейера сортировки и анализа. Решение в принципе почти тривиально.
Дело в том, что если приложение не привязано к ПК, а поток данных и обработка "совместимы" с решением FPGA (автономным или в виде карты сопроцессора в машине), то вы не сможете двигаться дальше. иметь возможность превзойти достижимый уровень производительности с помощью программного обеспечения, написанного на любом языке, независимо от алгоритма.
РЕДАКТИРОВАТЬ:
Просто запустил быстрый поиск и нашел бумагу, которая может быть вам полезна. Похоже, это восходит к 2012 году. Вы можете сделать намного лучше в производительности сегодня (и даже тогда). Вот:
Недавно я написал небольшой класс, который использует алгоритм Бозе-Нельсона для генерации сети сортировки во время компиляции.
С его помощью можно создать очень быструю сортировку по 10 числам.
/**
* A Functor class to create a sort for fixed sized arrays/containers with a
* compile time generated Bose-Nelson sorting network.
* \tparam NumElements The number of elements in the array or container to sort.
* \tparam T The element type.
* \tparam Compare A comparator functor class that returns true if lhs < rhs.
*/
template <unsigned NumElements, class Compare = void> class StaticSort
{
template <class A, class C> struct Swap
{
template <class T> inline void s(T &v0, T &v1)
{
T t = Compare()(v0, v1) ? v0 : v1; // Min
v1 = Compare()(v0, v1) ? v1 : v0; // Max
v0 = t;
}
inline Swap(A &a, const int &i0, const int &i1) { s(a[i0], a[i1]); }
};
template <class A> struct Swap <A, void>
{
template <class T> inline void s(T &v0, T &v1)
{
// Explicitly code out the Min and Max to nudge the compiler
// to generate branchless code.
T t = v0 < v1 ? v0 : v1; // Min
v1 = v0 < v1 ? v1 : v0; // Max
v0 = t;
}
inline Swap(A &a, const int &i0, const int &i1) { s(a[i0], a[i1]); }
};
template <class A, class C, int I, int J, int X, int Y> struct PB
{
inline PB(A &a)
{
enum { L = X >> 1, M = (X & 1 ? Y : Y + 1) >> 1, IAddL = I + L, XSubL = X - L };
PB<A, C, I, J, L, M> p0(a);
PB<A, C, IAddL, J + M, XSubL, Y - M> p1(a);
PB<A, C, IAddL, J, XSubL, M> p2(a);
}
};
template <class A, class C, int I, int J> struct PB <A, C, I, J, 1, 1>
{
inline PB(A &a) { Swap<A, C> s(a, I - 1, J - 1); }
};
template <class A, class C, int I, int J> struct PB <A, C, I, J, 1, 2>
{
inline PB(A &a) { Swap<A, C> s0(a, I - 1, J); Swap<A, C> s1(a, I - 1, J - 1); }
};
template <class A, class C, int I, int J> struct PB <A, C, I, J, 2, 1>
{
inline PB(A &a) { Swap<A, C> s0(a, I - 1, J - 1); Swap<A, C> s1(a, I, J - 1); }
};
template <class A, class C, int I, int M, bool Stop = false> struct PS
{
inline PS(A &a)
{
enum { L = M >> 1, IAddL = I + L, MSubL = M - L};
PS<A, C, I, L, (L <= 1)> ps0(a);
PS<A, C, IAddL, MSubL, (MSubL <= 1)> ps1(a);
PB<A, C, I, IAddL, L, MSubL> pb(a);
}
};
template <class A, class C, int I, int M> struct PS <A, C, I, M, true>
{
inline PS(A &a) {}
};
public:
/**
* Sorts the array/container arr.
* \param arr The array/container to be sorted.
*/
template <class Container> inline void operator() (Container &arr) const
{
PS<Container, Compare, 1, NumElements, (NumElements <= 1)> ps(arr);
};
/**
* Sorts the array arr.
* \param arr The array to be sorted.
*/
template <class T> inline void operator() (T *arr) const
{
PS<T*, Compare, 1, NumElements, (NumElements <= 1)> ps(arr);
};
};
#include <iostream>
#include <vector>
int main(int argc, const char * argv[])
{
enum { NumValues = 10 };
// Arrays
{
int rands[NumValues];
for (int i = 0; i < NumValues; ++i) rands[i] = rand() % 100;
std::cout << "Before Sort: \t";
for (int i = 0; i < NumValues; ++i) std::cout << rands[i] << " ";
std::cout << "\n";
StaticSort<NumValues> staticSort;
staticSort(rands);
std::cout << "After Sort: \t";
for (int i = 0; i < NumValues; ++i) std::cout << rands[i] << " ";
std::cout << "\n";
}
std::cout << "\n";
// STL Vector
{
std::vector<int> rands(NumValues);
for (int i = 0; i < NumValues; ++i) rands[i] = rand() % 100;
std::cout << "Before Sort: \t";
for (int i = 0; i < NumValues; ++i) std::cout << rands[i] << " ";
std::cout << "\n";
StaticSort<NumValues> staticSort;
staticSort(rands);
std::cout << "After Sort: \t";
for (int i = 0; i < NumValues; ++i) std::cout << rands[i] << " ";
std::cout << "\n";
}
return 0;
}
Обратите внимание, что вместо if (compare) swap утверждение, мы явно кодируем тернарные операторы для мин и макс. Это поможет подтолкнуть компилятор к использованию кода без ответвлений.
Ориентиры
Следующие тесты скомпилированы с помощью clang -O3 и запущены на моем MacBook Air в середине 2012 года.
Сортировка случайных данных
Сравнивая его с кодом DarioP, вот количество миллисекунд, потраченных на сортировку 1 миллиона 32-битных массивов int размером 10:
Жестко закодированная сортировка 10: 88,774 мс
Шаблон Бозе-Нельсона, сортировка 10: 27,815 мс
Используя этот шаблонный подход, мы также можем генерировать сети сортировки по времени компиляции для другого числа элементов.
Время (в миллисекундах) сортировать 1 миллион массивов разных размеров.
Количество миллисекунд для массивов размером 2, 4, 8 составляет 1,943, 8,655 и 20,246 соответственно. 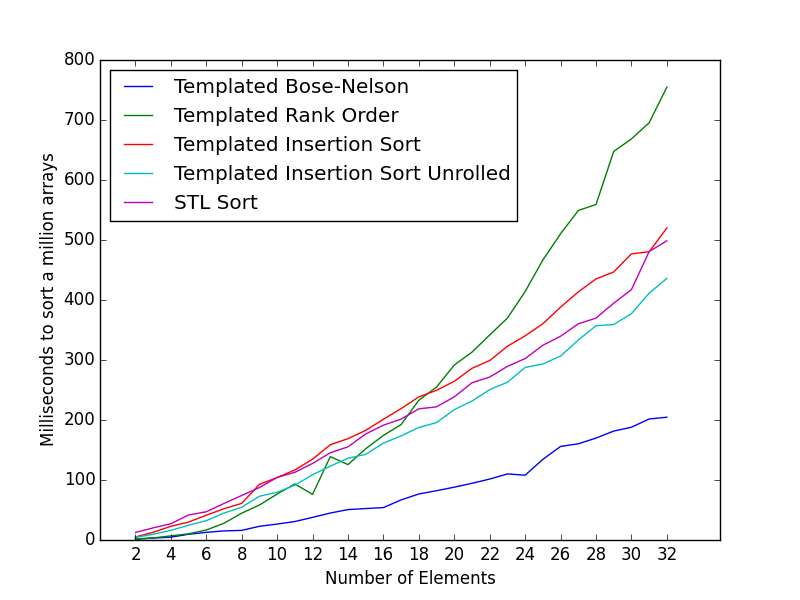
Кредиты Гленну Тейтельбауму для развернутого рода вставок.
Вот средние часы на сортировку для маленьких массивов из 6 элементов. Код теста и примеры можно найти по этому вопросу:
Самый быстрый вид массива с фиксированной длиной 6 int
Direct call to qsort library function : 326.81
Naive implementation (insertion sort) : 132.98
Insertion Sort (Daniel Stutzbach) : 104.04
Insertion Sort Unrolled : 99.64
Insertion Sort Unrolled (Glenn Teitelbaum) : 81.55
Rank Order : 44.01
Rank Order with registers : 42.40
Sorting Networks (Daniel Stutzbach) : 88.06
Sorting Networks (Paul R) : 31.64
Sorting Networks 12 with Fast Swap : 29.68
Sorting Networks 12 reordered Swap : 28.61
Reordered Sorting Network w/ fast swap : 24.63
Templated Sorting Network (this class) : 25.37
Он работает так же быстро, как самый быстрый пример в вопросе для 6 элементов.
Производительность по сортировке отсортированных данных
Часто входные массивы могут быть уже отсортированы или в основном отсортированы.
В таких случаях вставка сортировки может быть лучшим выбором.
Вы можете выбрать подходящий алгоритм сортировки в зависимости от данных.
Код, используемый для тестов, можно найти здесь.
Хотя сетевая сортировка имеет хорошие шансы быть быстрой на небольших массивах, иногда вы не сможете превзойти сортировку вставкой, если ее правильно оптимизировать. Например, пакетная вставка с 2 элементами:
{
final int a=in[0]<in[1]?in[0]:in[1];
final int b=in[0]<in[1]?in[1]:in[0];
in[0]=a;
in[1]=b;
}
for(int x=2;x<10;x+=2)
{
final int a=in[x]<in[x+1]?in[x]:in[x+1];
final int b=in[x]<in[x+1]?in[x+1]:in[x];
int y= x-1;
while(y>=0&&in[y]>b)
{
in[y+2]= in[y];
--y;
}
in[y+2]=b;
while(y>=0&&in[y]>a)
{
in[y+1]= in[y];
--y;
}
in[y+1]=a;
}
Вы можете полностью развернуть insertion sort
Чтобы сделать это проще, рекурсивный templates может использоваться без дополнительных служебных функций. Так как это уже template, int может быть template параметр также. Это также делает размеры массива кодирования, отличные от 10, тривиальными для создания.
Обратите внимание, что для сортировки int x[10] вызов insert_sort<int, 9>::sort(x); так как класс использует индекс последнего элемента. Это можно обернуть, но это будет больше кода для чтения.
template <class T, int NUM>
class insert_sort;
template <class T>
class insert_sort<T,0>
// stop template recursion
// sorting 1 item is a no-op
{
public:
static void place(T *x) {}
static void sort(T * x) {}
};
template <class T, int NUM>
class insert_sort
// use template recursion to do insertion sort
// NUM is the index of the last item, eg. for x[10] call <9>
{
public:
static void place(T *x)
{
T t1=x[NUM-1];
T t2=x[NUM];
if (t1 > t2)
{
x[NUM-1]=t2;
x[NUM]=t1;
insert_sort<T,NUM-1>::place(x);
}
}
static void sort(T * x)
{
insert_sort<T,NUM-1>::sort(x); // sort everything before
place(x); // put this item in
}
};
В моем тестировании это было быстрее, чем примеры сортировки сети.
По причинам, аналогичным тем, которые я описал здесь, следующие функции сортировки, sort6_iterator() а также sort10_iterator_local(), должно хорошо работать, откуда была взята сеть сортировки:
template<class IterType>
inline void sort10_iterator(IterType it)
{
#define SORT2(x,y) {if(data##x>data##y)std::swap(data##x,data##y);}
#define DD1(a) auto data##a=*(data+a);
#define DD2(a,b) auto data##a=*(data+a), data##b=*(data+b);
#define CB1(a) *(data+a)=data##a;
#define CB2(a,b) *(data+a)=data##a;*(data+b)=data##b;
DD2(1,4) SORT2(1,4) DD2(7,8) SORT2(7,8) DD2(2,3) SORT2(2,3) DD2(5,6) SORT2(5,6) DD2(0,9) SORT2(0,9)
SORT2(2,5) SORT2(0,7) SORT2(8,9) SORT2(3,6)
SORT2(4,9) SORT2(0,1)
SORT2(0,2) CB1(0) SORT2(6,9) CB1(9) SORT2(3,5) SORT2(4,7) SORT2(1,8)
SORT2(3,4) SORT2(5,8) SORT2(6,7) SORT2(1,2)
SORT2(7,8) CB1(8) SORT2(1,3) CB1(1) SORT2(2,5) SORT2(4,6)
SORT2(2,3) CB1(2) SORT2(6,7) CB1(7) SORT2(4,5)
SORT2(3,4) CB2(3,4) SORT2(5,6) CB2(5,6)
#undef CB1
#undef CB2
#undef DD1
#undef DD2
#undef SORT2
}
Чтобы вызвать эту функцию, я передал ей std::vector итератор.
Следующее ядро CUDA, работающее на 10 потоках CUDA (алгоритм ранговой сортировки), сортирует 1000 массивов 1000 раз за 42 миллисекунды, что составляет 42 наносекунды на сортировку или ~70 циклов (на частоте 1,7 ГГц) на сортировку:
inline
__device__ int findOrder(const int mask, const int data0)
{
const int order1 = data0>__shfl_sync(mask,data0,0);
const int order2 = data0>__shfl_sync(mask,data0,1);
const int order3 = data0>__shfl_sync(mask,data0,2);
const int order4 = data0>__shfl_sync(mask,data0,3);
const int order5 = data0>__shfl_sync(mask,data0,4);
const int order6 = data0>__shfl_sync(mask,data0,5);
const int order7 = data0>__shfl_sync(mask,data0,6);
const int order8 = data0>__shfl_sync(mask,data0,7);
const int order9 = data0>__shfl_sync(mask,data0,8);
const int order10 = data0>__shfl_sync(mask,data0,9);
return order1 + order2 + order3 + order4 + order5 + order6 + order7 + order8 + order9 + order10;
}
// launch this with 10 CUDA threads in 1 block in 1 grid
// sorts 10 elements using only SIMT registers
__global__ void rankSort(int * __restrict__ buffer)
{
const int id = threadIdx.x;
// enable first 10 lanes of warp for shuffling
const int mask = __activemask();
__shared__ int data[10000];
for(int i=0;i<1000;i++)
{
data[id+i*10] = buffer[id+i*10];
}
__syncwarp();
// benchmark 1000 times
for(int k=0;k<1000;k++)
{
// sort 1000 arrays
for(int j=0;j<1000;j+=5)
{
// sort 5 arrays at once to hide latency
const int data1 = data[id+j*10];
const int data2 = data[id+(j+1)*10];
const int data3 = data[id+(j+2)*10];
const int data4 = data[id+(j+3)*10];
const int data5 = data[id+(j+4)*10];
const int order1 = findOrder(mask,data1);
const int order2 = findOrder(mask,data2);
const int order3 = findOrder(mask,data3);
const int order4 = findOrder(mask,data4);
const int order5 = findOrder(mask,data5);
data[order1+j*10]=data1;
data[order2+(j+1)*10]=data2;
data[order3+(j+2)*10]=data3;
data[order4+(j+3)*10]=data4;
data[order5+(j+4)*10]=data5;
}
}
__syncwarp();
for(int i=0;i<1000;i++)
{
buffer[id+i*10] = data[id+i*10];
}
}
Поскольку все 10 потоков обрабатываются в одном SIMT-модуле, это похоже на оптимизированную версию AVX512, работающую на векторных регистрах, но за исключением гораздо большего регистрового пространства, чтобы скрыть большую задержку. Кроме того, блок SIMT имеет ширину 32, поэтому он может работать с линейной временной сложностью до 32 элементов.
Этот алгоритм предполагает, что элементы уникальны. Для повторяющихся данных требуется дополнительный шаг сокращения, чтобы распаковать повторяющиеся значения заказа до 10 элементов. Сначала он вычисляет ранг каждого элемента, а затем напрямую копирует их в их ранг как индекс в массиве. Значения порядка требуют грубой силы (O(N x N)) количества сравнений, и для уменьшения задержки используются варп-тасовки для сбора данных из разных варп-полос (векторного регистра).
Зачем менять местами, когда можно двигаться? В одной строке кэша x86 достаточно дополнительной памяти для выполнения сортировки слиянием.
Я бы, вероятно, вставил индексы сортировки 0–1, 2–4, 5–6, 7–9 по отдельности или, еще лучше, отсортировал эти маленькие группы, когда я делаю вставки, так что для каждой вставки требуется не более одной или двух смен.
Затем объедините 5,6 и 7-9 -> 10-14, объедините 0-1 и 2-4 -> 5-9 и, наконец, объедините 5-9 и 10-14 -> 0-9
Для сортировки вставкой требуется в среднем 29,6 сравнений для сортировки 10 входных данных с наилучшим регистром из 9 и худшим из 45 (с учетом входных данных в обратном порядке).
{9,6,1} Оболочка сортировки потребует в среднем 25,5 сравнений для сортировки 10 входных данных. Наилучший случай - 14 сравнений, наихудший - 34, а для сортировки обратного ввода требуется 22.
Таким образом, использование сортировки по типу оболочки вместо сортировки по вставке уменьшает средний регистр на 14%. Хотя лучший случай увеличен на 56%, худший случай уменьшен на 24%, что важно в приложениях, где важно контролировать производительность наихудшего случая. Обратный случай уменьшен на 51%.
Поскольку вы, похоже, знакомы с сортировкой вставок, вы можете реализовать алгоритм как сеть сортировки для {9,6}, а затем добавить сортировку вставок ({1}) после этого:
i[0] with i[9] // {9}
i[0] with i[6] // {6}
i[1] with i[7] // {6}
i[2] with i[8] // {6}
i[3] with i[9] // {6}
i[0 ... 9] // insertion sort