Какой самый быстрый способ получить значение π?
Я ищу самый быстрый способ получить значение π, как личный вызов. В частности, я использую способы, которые не связаны с использованием #define константы как M_PIили жестко закодировать число в.
Программа ниже проверяет различные способы, которые я знаю. Версия inline сборки, теоретически, является самым быстрым вариантом, хотя и явно не переносимым. Я включил его в качестве основы для сравнения с другими версиями. В моих тестах со встроенными 4 * atan(1) версия самая быстрая на GCC 4.2, потому что она автоматически сворачивает atan(1) в постоянную. С -fno-builtin указано, atan2(0, -1) версия самая быстрая.
Вот основная программа тестирования (pitimes.c):
#include <math.h>
#include <stdio.h>
#include <time.h>
#define ITERS 10000000
#define TESTWITH(x) { \
diff = 0.0; \
time1 = clock(); \
for (i = 0; i < ITERS; ++i) \
diff += (x) - M_PI; \
time2 = clock(); \
printf("%s\t=> %e, time => %f\n", #x, diff, diffclock(time2, time1)); \
}
static inline double
diffclock(clock_t time1, clock_t time0)
{
return (double) (time1 - time0) / CLOCKS_PER_SEC;
}
int
main()
{
int i;
clock_t time1, time2;
double diff;
/* Warmup. The atan2 case catches GCC's atan folding (which would
* optimise the ``4 * atan(1) - M_PI'' to a no-op), if -fno-builtin
* is not used. */
TESTWITH(4 * atan(1))
TESTWITH(4 * atan2(1, 1))
#if defined(__GNUC__) && (defined(__i386__) || defined(__amd64__))
extern double fldpi();
TESTWITH(fldpi())
#endif
/* Actual tests start here. */
TESTWITH(atan2(0, -1))
TESTWITH(acos(-1))
TESTWITH(2 * asin(1))
TESTWITH(4 * atan2(1, 1))
TESTWITH(4 * atan(1))
return 0;
}
И встроенная сборка мелочей (fldpi.c), который будет работать только для систем x86 и x64:
double
fldpi()
{
double pi;
asm("fldpi" : "=t" (pi));
return pi;
}
И скрипт сборки, который собирает все конфигурации, которые я тестирую (build.sh):
#!/bin/sh
gcc -O3 -Wall -c -m32 -o fldpi-32.o fldpi.c
gcc -O3 -Wall -c -m64 -o fldpi-64.o fldpi.c
gcc -O3 -Wall -ffast-math -m32 -o pitimes1-32 pitimes.c fldpi-32.o
gcc -O3 -Wall -m32 -o pitimes2-32 pitimes.c fldpi-32.o -lm
gcc -O3 -Wall -fno-builtin -m32 -o pitimes3-32 pitimes.c fldpi-32.o -lm
gcc -O3 -Wall -ffast-math -m64 -o pitimes1-64 pitimes.c fldpi-64.o -lm
gcc -O3 -Wall -m64 -o pitimes2-64 pitimes.c fldpi-64.o -lm
gcc -O3 -Wall -fno-builtin -m64 -o pitimes3-64 pitimes.c fldpi-64.o -lm
Помимо тестирования между различными флагами компилятора (я также сравнил 32-битные и 64-битные, потому что оптимизации разные), я также попытался изменить порядок тестов. Но все же, atan2(0, -1) версия по-прежнему выходит на первое место каждый раз.
27 ответов
В методе Монте-Карло, как уже упоминалось, применяются некоторые замечательные концепции, но он, очевидно, не самый быстрый, ни в дальнем плане, ни в какой-либо разумной мере. Кроме того, все зависит от того, какую точность вы ищете. Самый быстрый π, который я знаю, это тот, у которого цифры жестко запрограммированы. Глядя на Pi и Pi [PDF], есть много формул.
Вот метод, который быстро сходится - около 14 цифр за итерацию. PiFast, текущее самое быстрое приложение, использует эту формулу с БПФ. Я просто напишу формулу, так как код прост. Эта формула была почти найдена Рамануджаном и открыта Чудновским. Это на самом деле, как он вычислил несколько миллиардов цифр числа, так что это не метод игнорировать. Формула будет быстро переполнена, и, поскольку мы делим факториалы, было бы целесообразно отложить такие вычисления, чтобы удалить термины.
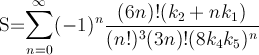
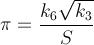
где,
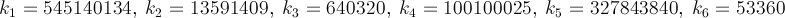
Ниже приведен алгоритм Брента – Саламина. В Википедии упоминается, что когда a и b "достаточно близки", тогда (a + b)² / 4t будет приближением π. Я не уверен, что означает "достаточно близко", но из моих тестов одна итерация получила 2 цифры, две - 7, а три - 15, конечно это с двойными числами, поэтому может возникнуть ошибка, основанная на ее представлении и истинный расчет может быть более точным.
let pi_2 iters =
let rec loop_ a b t p i =
if i = 0 then a,b,t,p
else
let a_n = (a +. b) /. 2.0
and b_n = sqrt (a*.b)
and p_n = 2.0 *. p in
let t_n = t -. (p *. (a -. a_n) *. (a -. a_n)) in
loop_ a_n b_n t_n p_n (i - 1)
in
let a,b,t,p = loop_ (1.0) (1.0 /. (sqrt 2.0)) (1.0/.4.0) (1.0) iters in
(a +. b) *. (a +. b) /. (4.0 *. t)
Наконец, как насчет пи-гольфа (800 цифр)? 160 символов!
int a=10000,b,c=2800,d,e,f[2801],g;main(){for(;b-c;)f[b++]=a/5;for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);}
Мне очень нравится эта программа, потому что она аппроксимирует π, глядя на свою область.
IOCCC 1988: westley.c
#define _ -F<00||--F-OO--; int F=00,OO=00;main(){F_OO();printf("%1.3f\n",4.*-F/OO/OO);}F_OO() { _-_-_-_ _-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_-_-_-_-_ _-_-_-_-_-_-_-_ _-_-_-_ }
Вот общее описание методики расчета пи, которую я выучил в старшей школе.
Я делюсь этим только потому, что думаю, что это достаточно просто, чтобы каждый мог помнить об этом на неопределенный срок, плюс он учит вас концепции методов "Монте-Карло" - статистических методов получения ответов, которые не сразу кажутся выводимые через случайные процессы.
Нарисуйте квадрат и вписайте квадрант (одну четверть полукруга) внутри этого квадрата (квадрант с радиусом, равным стороне квадрата, чтобы он заполнил как можно большую часть квадрата)
Теперь бросьте дротик в квадрат и запишите, где он приземлится, то есть выберите случайную точку в любом месте квадрата. Конечно, он приземлился внутри квадрата, но внутри полукруга? Запишите этот факт.
Повторите этот процесс много раз - и вы обнаружите, что есть отношение количества точек внутри полукруга к общему выброшенному количеству, назовите это соотношение x.
Так как площадь квадрата r раз r, вы можете сделать вывод, что площадь полукруга равна x раз r раз r (то есть x умножается на квадрат). Следовательно, х раз 4 даст вам пи.
Это не быстрый метод для использования. Но это хороший пример метода Монте-Карло. И если вы посмотрите вокруг, вы можете обнаружить, что с помощью этих методов можно решить многие проблемы, не относящиеся к вашим вычислительным навыкам.
В интересах полноты, версия шаблона C++, которая для оптимизированной сборки будет вычислять приближение PI во время компиляции и будет встроена в одно значение.
#include <iostream>
template<int I>
struct sign
{
enum {value = (I % 2) == 0 ? 1 : -1};
};
template<int I, int J>
struct pi_calc
{
inline static double value ()
{
return (pi_calc<I-1, J>::value () + pi_calc<I-1, J+1>::value ()) / 2.0;
}
};
template<int J>
struct pi_calc<0, J>
{
inline static double value ()
{
return (sign<J>::value * 4.0) / (2.0 * J + 1.0) + pi_calc<0, J-1>::value ();
}
};
template<>
struct pi_calc<0, 0>
{
inline static double value ()
{
return 4.0;
}
};
template<int I>
struct pi
{
inline static double value ()
{
return pi_calc<I, I>::value ();
}
};
int main ()
{
std::cout.precision (12);
const double pi_value = pi<10>::value ();
std::cout << "pi ~ " << pi_value << std::endl;
return 0;
}
Обратите внимание, что для I > 10 оптимизированные сборки могут выполняться медленно, также как и для неоптимизированных запусков. Я полагаю, что для 12 итераций существует около 80 тыс. Вызовов value() (при отсутствии запоминания).
На самом деле есть целая книга, посвященная (среди прочего) быстрым методам вычисления \pi: 'Pi и AGM' Джонатаном и Питером Боровейном ( доступно на Amazon).
Я немного изучил AGM и связанные с ним алгоритмы: это довольно интересно (хотя иногда нетривиально).
Обратите внимание, что для реализации большинства современных алгоритмов для вычисления \ pi вам понадобится многоточная арифметическая библиотека ( GMP - неплохой выбор, хотя я давно его использовал).
Временная сложность лучших алгоритмов находится в O (M(n) log (n)), где M(n) - временная сложность для умножения двух n-битных целых чисел (M(n)=O(n). log (n) log (log (n))) с использованием алгоритмов на основе FFT, которые обычно необходимы при вычислении цифр \pi, и такой алгоритм реализован в GMP).
Обратите внимание, что хотя математика, лежащая в основе алгоритмов, может и не быть тривиальной, сами алгоритмы обычно представляют собой несколько строк псевдокода, и их реализация обычно очень проста (если вы решили не писать свою собственную арифметику множественности точности:-)).
Ниже приводится точный ответ, как сделать это максимально быстрым способом - с наименьшими вычислительными затратами. Даже если вам не нравится ответ, вы должны признать, что это действительно самый быстрый способ получить значение PI.
Самый быстрый способ получить значение Pi:
- выбрал свой любимый язык программирования
- загрузить это математическая библиотека
- и найти, что Пи уже определен там!! готов использовать это..
если у вас нет библиотеки математики под рукой..
ВТОРОЙ БЫСТРЫЙ способ (более универсальное решение) это:
найдите Пи в Интернете, например, здесь:
http://www.eveandersson.com/pi/digits/1000000 (1 миллион цифр.. какова ваша точность с плавающей запятой?)
или здесь:
http://3.141592653589793238462643383279502884197169399375105820974944592.com/
или здесь:
http://en.wikipedia.org/wiki/Pi
Очень быстро найти нужные цифры для любой точной арифметики, которую вы хотели бы использовать, и, определяя константу, вы можете быть уверены, что не тратите драгоценное время процессора.
Это не только отчасти юмористический ответ, но на самом деле, если бы кто-то пошел дальше и вычислил значение Pi в реальном приложении... это было бы довольно большой тратой процессорного времени, не так ли? По крайней мере, я не вижу реального приложения для попытки пересчитать это.
Уважаемый Модератор: обратите внимание, что ОП спросил: "Самый быстрый способ получить значение ПИ"
Формула BBP позволяет вычислять n-ую цифру - в базе 2 (или 16) - без необходимости сначала беспокоиться о предыдущих n-1 цифрах:)
Это "классический" метод, очень простой в реализации. Эта реализация в Python (не очень быстрый язык) делает это:
from math import pi
from time import time
precision = 10**6 # higher value -> higher precision
# lower value -> higher speed
t = time()
calc = 0
for k in xrange(0, precision):
calc += ((-1)**k) / (2*k+1.)
calc *= 4. # this is just a little optimization
t = time()-t
print "Calculated: %.40f" % calc
print "Costant pi: %.40f" % pi
print "Difference: %.40f" % abs(calc-pi)
print "Time elapsed: %s" % repr(t)
Вы можете найти больше информации здесь.
В любом случае, самый быстрый способ получить точное число пи в python:
from gmpy import pi
print pi(3000) # the rule is the same as
# the precision on the previous code
Вот часть исходного кода для метода gmpy pi, я не думаю, что код так же полезен, как комментарий в этом случае:
static char doc_pi[]="\
pi(n): returns pi with n bits of precision in an mpf object\n\
";
/* This function was originally from netlib, package bmp, by
* Richard P. Brent. Paulo Cesar Pereira de Andrade converted
* it to C and used it in his LISP interpreter.
*
* Original comments:
*
* sets mp pi = 3.14159... to the available precision.
* uses the gauss-legendre algorithm.
* this method requires time o(ln(t)m(t)), so it is slower
* than mppi if m(t) = o(t**2), but would be faster for
* large t if a faster multiplication algorithm were used
* (see comments in mpmul).
* for a description of the method, see - multiple-precision
* zero-finding and the complexity of elementary function
* evaluation (by r. p. brent), in analytic computational
* complexity (edited by j. f. traub), academic press, 1976, 151-176.
* rounding options not implemented, no guard digits used.
*/
static PyObject *
Pygmpy_pi(PyObject *self, PyObject *args)
{
PympfObject *pi;
int precision;
mpf_t r_i2, r_i3, r_i4;
mpf_t ix;
ONE_ARG("pi", "i", &precision);
if(!(pi = Pympf_new(precision))) {
return NULL;
}
mpf_set_si(pi->f, 1);
mpf_init(ix);
mpf_set_ui(ix, 1);
mpf_init2(r_i2, precision);
mpf_init2(r_i3, precision);
mpf_set_d(r_i3, 0.25);
mpf_init2(r_i4, precision);
mpf_set_d(r_i4, 0.5);
mpf_sqrt(r_i4, r_i4);
for (;;) {
mpf_set(r_i2, pi->f);
mpf_add(pi->f, pi->f, r_i4);
mpf_div_ui(pi->f, pi->f, 2);
mpf_mul(r_i4, r_i2, r_i4);
mpf_sub(r_i2, pi->f, r_i2);
mpf_mul(r_i2, r_i2, r_i2);
mpf_mul(r_i2, r_i2, ix);
mpf_sub(r_i3, r_i3, r_i2);
mpf_sqrt(r_i4, r_i4);
mpf_mul_ui(ix, ix, 2);
/* Check for convergence */
if (!(mpf_cmp_si(r_i2, 0) &&
mpf_get_prec(r_i2) >= (unsigned)precision)) {
mpf_mul(pi->f, pi->f, r_i4);
mpf_div(pi->f, pi->f, r_i3);
break;
}
}
mpf_clear(ix);
mpf_clear(r_i2);
mpf_clear(r_i3);
mpf_clear(r_i4);
return (PyObject*)pi;
}
РЕДАКТИРОВАТЬ: У меня были некоторые проблемы с вырезать и вставить и идентификации, в любом случае вы можете найти источник здесь.
Вместо того, чтобы определять пи как константу, я всегда использую acos(-1),
Если эта статья верна, то алгоритм, который создал Беллард, может быть одним из самых быстрых из доступных. Он создал пи до 2,7 триллиона цифр с помощью настольного ПК!
... и он опубликовал свою работу здесь
Хорошая работа, Беллард, ты пионер!
Просто наткнулся на этот, который должен быть здесь для полноты:
У него есть довольно приятное свойство: точность можно повысить, увеличив программу.
Вот немного понимания самого языка
Используйте формулу, подобную Machin
176 * arctan (1/57) + 28 * arctan (1/239) - 48 * arctan (1/682) + 96 * arctan(1/12943)
[; \left( 176 \arctan \frac{1}{57} + 28 \arctan \frac{1}{239} - 48 \arctan \frac{1}{682} + 96 \arctan \frac{1}{12943}\right) ;], for you TeX the World people.
Реализовано в схеме, например:
(+ (- (+ (* 176 (atan (/ 1 57))) (* 28 (atan (/ 1 239)))) (* 48 (atan (/ 1 682)))) (* 96 (atan (/ 1 12943))))
Если вы хотите использовать приближение, 355 / 113 подходит для 6 десятичных цифр и имеет дополнительное преимущество, заключающееся в возможности использования с целочисленными выражениями. Это не так важно в наши дни, так как "математический сопроцессор с плавающей запятой" перестал иметь какое-либо значение, но когда-то это было довольно важно.
Пи ровно 3! [Профессор Фринк (Симпсоны)]
Шутка, но вот один в C# (требуется.NET-Framework).
using System;
using System.Text;
class Program {
static void Main(string[] args) {
int Digits = 100;
BigNumber x = new BigNumber(Digits);
BigNumber y = new BigNumber(Digits);
x.ArcTan(16, 5);
y.ArcTan(4, 239);
x.Subtract(y);
string pi = x.ToString();
Console.WriteLine(pi);
}
}
public class BigNumber {
private UInt32[] number;
private int size;
private int maxDigits;
public BigNumber(int maxDigits) {
this.maxDigits = maxDigits;
this.size = (int)Math.Ceiling((float)maxDigits * 0.104) + 2;
number = new UInt32[size];
}
public BigNumber(int maxDigits, UInt32 intPart)
: this(maxDigits) {
number[0] = intPart;
for (int i = 1; i < size; i++) {
number[i] = 0;
}
}
private void VerifySameSize(BigNumber value) {
if (Object.ReferenceEquals(this, value))
throw new Exception("BigNumbers cannot operate on themselves");
if (value.size != this.size)
throw new Exception("BigNumbers must have the same size");
}
public void Add(BigNumber value) {
VerifySameSize(value);
int index = size - 1;
while (index >= 0 && value.number[index] == 0)
index--;
UInt32 carry = 0;
while (index >= 0) {
UInt64 result = (UInt64)number[index] +
value.number[index] + carry;
number[index] = (UInt32)result;
if (result >= 0x100000000U)
carry = 1;
else
carry = 0;
index--;
}
}
public void Subtract(BigNumber value) {
VerifySameSize(value);
int index = size - 1;
while (index >= 0 && value.number[index] == 0)
index--;
UInt32 borrow = 0;
while (index >= 0) {
UInt64 result = 0x100000000U + (UInt64)number[index] -
value.number[index] - borrow;
number[index] = (UInt32)result;
if (result >= 0x100000000U)
borrow = 0;
else
borrow = 1;
index--;
}
}
public void Multiply(UInt32 value) {
int index = size - 1;
while (index >= 0 && number[index] == 0)
index--;
UInt32 carry = 0;
while (index >= 0) {
UInt64 result = (UInt64)number[index] * value + carry;
number[index] = (UInt32)result;
carry = (UInt32)(result >> 32);
index--;
}
}
public void Divide(UInt32 value) {
int index = 0;
while (index < size && number[index] == 0)
index++;
UInt32 carry = 0;
while (index < size) {
UInt64 result = number[index] + ((UInt64)carry << 32);
number[index] = (UInt32)(result / (UInt64)value);
carry = (UInt32)(result % (UInt64)value);
index++;
}
}
public void Assign(BigNumber value) {
VerifySameSize(value);
for (int i = 0; i < size; i++) {
number[i] = value.number[i];
}
}
public override string ToString() {
BigNumber temp = new BigNumber(maxDigits);
temp.Assign(this);
StringBuilder sb = new StringBuilder();
sb.Append(temp.number[0]);
sb.Append(System.Globalization.CultureInfo.CurrentCulture.NumberFormat.CurrencyDecimalSeparator);
int digitCount = 0;
while (digitCount < maxDigits) {
temp.number[0] = 0;
temp.Multiply(100000);
sb.AppendFormat("{0:D5}", temp.number[0]);
digitCount += 5;
}
return sb.ToString();
}
public bool IsZero() {
foreach (UInt32 item in number) {
if (item != 0)
return false;
}
return true;
}
public void ArcTan(UInt32 multiplicand, UInt32 reciprocal) {
BigNumber X = new BigNumber(maxDigits, multiplicand);
X.Divide(reciprocal);
reciprocal *= reciprocal;
this.Assign(X);
BigNumber term = new BigNumber(maxDigits);
UInt32 divisor = 1;
bool subtractTerm = true;
while (true) {
X.Divide(reciprocal);
term.Assign(X);
divisor += 2;
term.Divide(divisor);
if (term.IsZero())
break;
if (subtractTerm)
this.Subtract(term);
else
this.Add(term);
subtractTerm = !subtractTerm;
}
}
}
С двойниками:
4.0 * (4.0 * Math.Atan(0.2) - Math.Atan(1.0 / 239.0))
Это будет с точностью до 14 знаков после запятой, что достаточно для заполнения двойного числа (неточность, вероятно, связана с тем, что остальные десятичные знаки в арктангенсах усекаются).
Также Сет, это 3,141592653589793238463, а не 64.
Рассчитать PI во время компиляции с D.
(Скопировано с DSource.org)
/** Calculate pi at compile time
*
* Compile with dmd -c pi.d
*/
module calcpi;
import meta.math;
import meta.conv;
/** real evaluateSeries!(real x, real metafunction!(real y, int n) term)
*
* Evaluate a power series at compile time.
*
* Given a metafunction of the form
* real term!(real y, int n),
* which gives the nth term of a convergent series at the point y
* (where the first term is n==1), and a real number x,
* this metafunction calculates the infinite sum at the point x
* by adding terms until the sum doesn't change any more.
*/
template evaluateSeries(real x, alias term, int n=1, real sumsofar=0.0)
{
static if (n>1 && sumsofar == sumsofar + term!(x, n+1)) {
const real evaluateSeries = sumsofar;
} else {
const real evaluateSeries = evaluateSeries!(x, term, n+1, sumsofar + term!(x, n));
}
}
/*** Calculate atan(x) at compile time.
*
* Uses the Maclaurin formula
* atan(z) = z - z^3/3 + Z^5/5 - Z^7/7 + ...
*/
template atan(real z)
{
const real atan = evaluateSeries!(z, atanTerm);
}
template atanTerm(real x, int n)
{
const real atanTerm = (n & 1 ? 1 : -1) * pow!(x, 2*n-1)/(2*n-1);
}
/// Machin's formula for pi
/// pi/4 = 4 atan(1/5) - atan(1/239).
pragma(msg, "PI = " ~ fcvt!(4.0 * (4*atan!(1/5.0) - atan!(1/239.0))) );
В этой версии (в Delphi) нет ничего особенного, но она, по крайней мере, быстрее, чем версия, которую Ник Ходж опубликовал в своем блоге:). На моей машине около миллиарда итераций занимает около 16 секунд, что дает значение 3,14159265 25879 (точная часть выделена жирным шрифтом).
program calcpi;
{$APPTYPE CONSOLE}
uses
SysUtils;
var
start, finish: TDateTime;
function CalculatePi(iterations: integer): double;
var
numerator, denominator, i: integer;
sum: double;
begin
{
PI may be approximated with this formula:
4 * (1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 .......)
//}
numerator := 1;
denominator := 1;
sum := 0;
for i := 1 to iterations do begin
sum := sum + (numerator/denominator);
denominator := denominator + 2;
numerator := -numerator;
end;
Result := 4 * sum;
end;
begin
try
start := Now;
WriteLn(FloatToStr(CalculatePi(StrToInt(ParamStr(1)))));
finish := Now;
WriteLn('Seconds:' + FormatDateTime('hh:mm:ss.zz',finish-start));
except
on E:Exception do
Writeln(E.Classname, ': ', E.Message);
end;
end.
В прежние времена, с маленькими размерами слов и медленными или несуществующими операциями с плавающей запятой, мы делали что-то вроде этого:
/* Return approximation of n * PI; n is integer */
#define pi_times(n) (((n) * 22) / 7)
Для приложений, которые не требуют большой точности (например, видеоигры), это очень быстро и достаточно точно.
Если вы хотите вычислить аппроксимацию значения π (по некоторым причинам), вам следует попробовать алгоритм двоичного извлечения. Улучшение BBP Белларда дает ли PI в O(N^2).
Если вы хотите получить аппроксимацию значения π для выполнения расчетов, то:
PI = 3.141592654
Конечно, это только приблизительное значение, и не совсем точное. Это немного больше, чем 0,00000000004102. (четыре десять триллионных, около 4/10 000 000 000).
Если вы хотите заняться математикой с π, то возьмите себе карандаш и бумагу или пакет компьютерной алгебры и используйте точное значение π, π.
Если вы действительно хотите формулу, это весело:
π = - i ln (-1)
Метод Брента, опубликованный Крисом выше, очень хорош; Брент обычно является гигантом в области арифметики произвольной точности.
Если вам нужна только N-ая цифра, известная формула BBP полезна в шестнадцатеричном виде.
В основном ответ оптимизатора скрепок для C и гораздо более упрощенный:
#include <stdio.h>
#include <math.h>
double calc_PI(int K) {
static const int A = 545140134;
static const int B = 13591409;
static const int D = 640320;
const double ID3 = 1.0 / ((double) D * (double) D * (double) D);
double sum = 0.0;
double b = sqrt(ID3);
long long int p = 1;
long long int a = B;
sum += (double) p * (double) a * b;
for (int k = 1; k < K; ++k) {
a += A;
b *= ID3;
p *= (6 * k) * (6 * k - 1) * (6 * k - 2) * (6 * k - 3) * (6 * k - 4) * (6 * k - 5);
p /= (3 * k) * (3 * k - 1) * (3 * k - 2) * k * k * k;
p = -p;
sum += (double) p * (double) a * b;
}
return 1.0 / (12 * sum);
}
int main() {
for (int k = 1; k <= 5; ++k) {
printf("k = %i, PI = %.16f\n", k, calc_PI(k));
}
}
Но для большего упрощения этот алгоритм использует формулу Чудновского, которую я могу полностью упростить, если вы действительно не понимаете код.
Резюме: мы получим число от 1 до 5 и добавим его в функцию, которую мы будем использовать для получения PI. Затем вам дается 3 числа: 545140134 (A), 13591409 (B), 640320 (D). Тогда мы будем использовать D как
double умножение себя 3 раза на другое
double(ID3). Затем мы возьмем квадратный корень из ID3 в другой
double(b) и присвойте 2 числа: 1 (p), значение B (a). Обратите внимание, что C не чувствителен к регистру. Потом
double (сумма) будет создана путем умножения значений p, a и b, все в
doubleс. Затем цикл до тех пор, пока число, указанное для функции, не запустится и добавит значение A к a, значение b будет умножено на ID3, значение p будет умножено на несколько значений, которые, я надеюсь, вы поймете, а также разделится на несколько значений как хорошо. Сумма снова сложится на p, a и b, и цикл будет повторяться до тех пор, пока значение номера цикла не станет больше или равно 5. Позже сумма умножается на 12 и возвращается функцией, дающей нам результат ПИ.
Ладно, это было долго, но я думаю, вы это поймете...
Алгоритм Чудновского довольно быстр, если вы не против вычисления квадратного корня и пары обратных чисел. Он сходится к двойной точности всего за 2 итерации.
/*
Chudnovsky algorithm for computing PI
*/
#include <iostream>
#include <cmath>
using namespace std;
double calc_PI(int K=2) {
static const int A = 545140134;
static const int B = 13591409;
static const int D = 640320;
const double ID3 = 1./ (double(D)*double(D)*double(D));
double sum = 0.;
double b = sqrt(ID3);
long long int p = 1;
long long int a = B;
sum += double(p) * double(a)* b;
// 2 iterations enough for double convergence
for (int k=1; k<K; ++k) {
// A*k + B
a += A;
// update denominator
b *= ID3;
// p = (-1)^k 6k! / 3k! k!^3
p *= (6*k)*(6*k-1)*(6*k-2)*(6*k-3)*(6*k-4)*(6*k-5);
p /= (3*k)*(3*k-1)*(3*k-2) * k*k*k;
p = -p;
sum += double(p) * double(a)* b;
}
return 1./(12*sum);
}
int main() {
cout.precision(16);
cout.setf(ios::fixed);
for (int k=1; k<=5; ++k) cout << "k = " << k << " PI = " << calc_PI(k) << endl;
return 0;
}
Полученные результаты:
k = 1 PI = 3.1415926535897341
k = 2 PI = 3.1415926535897931
k = 3 PI = 3.1415926535897931
k = 4 PI = 3.1415926535897931
k = 5 PI = 3.1415926535897931
Вычисление π из площади круга:-)
<input id="range" type="range" min="10" max="960" value="10" step="50" oninput="calcPi()">
<br>
<div id="cont"></div>
<script>
function generateCircle(width) {
var c = width/2;
var delta = 1.0;
var str = "";
var xCount = 0;
for (var x=0; x <= width; x++) {
for (var y = 0; y <= width; y++) {
var d = Math.sqrt((x-c)*(x-c) + (y-c)*(y-c));
if (d > (width-1)/2) {
str += '.';
}
else {
xCount++;
str += 'o';
}
str += " "
}
str += "\n";
}
var pi = (xCount * 4) / (width * width);
return [str, pi];
}
function calcPi() {
var e = document.getElementById("cont");
var width = document.getElementById("range").value;
e.innerHTML = "<h4>Generating circle...</h4>";
setTimeout(function() {
var circ = generateCircle(width);
e.innerHTML = "<pre>" + "π = " + circ[1].toFixed(2) + "\n" + circ[0] +"</pre>";
}, 200);
}
calcPi();
</script>Я думаю, что значение пи - это отношение длины окружности к радиусу круга.
Это может быть просто достигнуто с помощью обычного математического расчета.
Быстрее, чем встроенные модули GMPY2 и MPmath: миллиард за 45 минут:
Я пробовал несколько способов; Manchin, AGM и Chudnovsky Bros. Чудновский с Binary Split был самым быстрым:
Мой github: https://github.com/Overboard-code/Pi-Pourri
Мой Binary Split Chudnovsky примерно в два раза быстрее встроенного gmpy2.const_pi(). MPmath.mp.pi() потребовалось 50 минут для миллиарда, так что это было почти так же быстро, как Чудновский.
Я также был бы очень признателен за советы по производительности. Я не уверен, что мой код идеален. Это на 100% точно (все формулы сходятся на 100 миллионов), но, может быть, могло бы быть быстрее?
Я попробовал gmpy2.const_pi() до 100 миллионов цифр, и это заняло 300 секунд против 150 секунд для Чудновского на той же машине. pi.txt и pi2.txt были одинаковыми.
На своем старом ноутбуке i7 16 ГБ я набрал миллиард цифр менее чем за час.
Вот фрагмент самого быстрого из 12 методов, которые я пробовал:
class PiChudnovsky:
"""Version of Chudnovsky Bros using Binary Splitting
So far this is the winner for fastest time to a million digits on my older intel i7
"""
A = mpz(13591409)
B = mpz(545140134)
C = mpz(640320)
D = mpz(426880)
E = mpz(10005)
C3_24 = pow(C, mpz(3)) // mpz(24)
#DIGITS_PER_TERM = math.log(53360 ** 3) / math.log(10) #=> 14.181647462725476
DIGITS_PER_TERM = 14.181647462725476
MMILL = mpz(1000000)
def __init__(self,ndigits):
""" Initialization
:param int ndigits: digits of PI computation
"""
self.ndigits = ndigits
self.n = mpz(self.ndigits // self.DIGITS_PER_TERM + 1)
self.prec = mpz((self.ndigits + 1) * LOG2_10)
self.one_sq = pow(mpz(10),mpz(2 * ndigits))
self.sqrt_c = isqrt(self.E * self.one_sq)
self.iters = mpz(0)
self.start_time = 0
def compute(self):
""" Computation """
try:
self.start_time = time.time()
logging.debug("Starting {} formula to {:,} decimal places"
.format(name,ndigits) )
__, q, t = self.__bs(mpz(0), self.n) # p is just for recursion
pi = (q * self.D * self.sqrt_c) // t
logging.debug('{} calulation Done! {:,} iterations and {:.2f} seconds.'
.format( name, int(self.iters),time.time() - self.start_time))
get_context().precision= int((self.ndigits+10) * LOG2_10)
pi_s = pi.digits() # digits() gmpy2 creates a string
pi_o = pi_s[:1] + "." + pi_s[1:]
return pi_o,int(self.iters),time.time() - self.start_time
except Exception as e:
print (e.message, e.args)
raise
def __bs(self, a, b):
""" PQT computation by BSA(= Binary Splitting Algorithm)
:param int a: positive integer
:param int b: positive integer
:return list [int p_ab, int q_ab, int t_ab]
"""
try:
self.iters += mpz(1)
if self.iters % self.MMILL == mpz(0):
logging.debug('Chudnovsky ... {:,} iterations and {:.2f} seconds.'
.format( int(self.iters),time.time() - self.start_time))
if a + mpz(1) == b:
if a == mpz(0):
p_ab = q_ab = mpz(1)
else:
p_ab = mpz((mpz(6) * a - mpz(5)) * (mpz(2) * a - mpz(1)) * (mpz(6) * a - mpz(1)))
q_ab = pow(a,mpz(3)) * self.C3_24
t_ab = p_ab * (self.A + self.B * a)
if a & 1:
t_ab *= mpz(-1)
else:
m = (a + b) // mpz(2)
p_am, q_am, t_am = self.__bs(a, m)
p_mb, q_mb, t_mb = self.__bs(m, b)
p_ab = p_am * p_mb
q_ab = q_am * q_mb
t_ab = q_mb * t_am + p_am * t_mb
return [p_ab, q_ab, t_ab]
except Exception as e:
print (e.message, e.args)
raise
Вот вывод 1 000 000 000 цифр менее чем за 45 минут:
python pi-pourri.py -v -d 1,000,000,000 -a 10
[INFO] 2022-10-03 09:22:51,860 <module>: MainProcess Computing π to 1,000,000,000 digits.
[DEBUG] 2022-10-03 09:25:00,543 compute: MainProcess Starting Chudnovsky brothers 1988
π = (Q(0, N) / 12T(0, N) + 12AQ(0, N))**(C**(3/2))
formula to 1,000,000,000 decimal places
[DEBUG] 2022-10-03 09:25:04,995 __bs: MainProcess Chudnovsky ... 1,000,000 iterations and 4.45 seconds.
[DEBUG] 2022-10-03 09:25:10,836 __bs: MainProcess Chudnovsky ... 2,000,000 iterations and 10.29 seconds.
[DEBUG] 2022-10-03 09:25:18,227 __bs: MainProcess Chudnovsky ... 3,000,000 iterations and 17.68 seconds.
[DEBUG] 2022-10-03 09:25:24,512 __bs: MainProcess Chudnovsky ... 4,000,000 iterations and 23.97 seconds.
[DEBUG] 2022-10-03 09:25:35,670 __bs: MainProcess Chudnovsky ... 5,000,000 iterations and 35.13 seconds.
[DEBUG] 2022-10-03 09:25:41,376 __bs: MainProcess Chudnovsky ... 6,000,000 iterations and 40.83 seconds.
[DEBUG] 2022-10-03 09:25:49,238 __bs: MainProcess Chudnovsky ... 7,000,000 iterations and 48.69 seconds.
[DEBUG] 2022-10-03 09:25:55,646 __bs: MainProcess Chudnovsky ... 8,000,000 iterations and 55.10 seconds.
[DEBUG] 2022-10-03 09:26:15,043 __bs: MainProcess Chudnovsky ... 9,000,000 iterations and 74.50 seconds.
[DEBUG] 2022-10-03 09:26:21,437 __bs: MainProcess Chudnovsky ... 10,000,000 iterations and 80.89 seconds.
[DEBUG] 2022-10-03 09:26:26,587 __bs: MainProcess Chudnovsky ... 11,000,000 iterations and 86.04 seconds.
[DEBUG] 2022-10-03 09:26:34,777 __bs: MainProcess Chudnovsky ... 12,000,000 iterations and 94.23 seconds.
[DEBUG] 2022-10-03 09:26:41,231 __bs: MainProcess Chudnovsky ... 13,000,000 iterations and 100.69 seconds.
[DEBUG] 2022-10-03 09:26:52,972 __bs: MainProcess Chudnovsky ... 14,000,000 iterations and 112.43 seconds.
[DEBUG] 2022-10-03 09:26:59,517 __bs: MainProcess Chudnovsky ... 15,000,000 iterations and 118.97 seconds.
[DEBUG] 2022-10-03 09:27:07,932 __bs: MainProcess Chudnovsky ... 16,000,000 iterations and 127.39 seconds.
[DEBUG] 2022-10-03 09:27:14,036 __bs: MainProcess Chudnovsky ... 17,000,000 iterations and 133.49 seconds.
[DEBUG] 2022-10-03 09:27:51,629 __bs: MainProcess Chudnovsky ... 18,000,000 iterations and 171.09 seconds.
[DEBUG] 2022-10-03 09:27:58,176 __bs: MainProcess Chudnovsky ... 19,000,000 iterations and 177.63 seconds.
[DEBUG] 2022-10-03 09:28:06,704 __bs: MainProcess Chudnovsky ... 20,000,000 iterations and 186.16 seconds.
[DEBUG] 2022-10-03 09:28:13,376 __bs: MainProcess Chudnovsky ... 21,000,000 iterations and 192.83 seconds.
[DEBUG] 2022-10-03 09:28:18,737 __bs: MainProcess Chudnovsky ... 22,000,000 iterations and 198.19 seconds.
[DEBUG] 2022-10-03 09:28:31,095 __bs: MainProcess Chudnovsky ... 23,000,000 iterations and 210.55 seconds.
[DEBUG] 2022-10-03 09:28:37,789 __bs: MainProcess Chudnovsky ... 24,000,000 iterations and 217.25 seconds.
[DEBUG] 2022-10-03 09:28:46,171 __bs: MainProcess Chudnovsky ... 25,000,000 iterations and 225.63 seconds.
[DEBUG] 2022-10-03 09:28:52,933 __bs: MainProcess Chudnovsky ... 26,000,000 iterations and 232.39 seconds.
[DEBUG] 2022-10-03 09:29:13,524 __bs: MainProcess Chudnovsky ... 27,000,000 iterations and 252.98 seconds.
[DEBUG] 2022-10-03 09:29:19,676 __bs: MainProcess Chudnovsky ... 28,000,000 iterations and 259.13 seconds.
[DEBUG] 2022-10-03 09:29:28,196 __bs: MainProcess Chudnovsky ... 29,000,000 iterations and 267.65 seconds.
[DEBUG] 2022-10-03 09:29:34,720 __bs: MainProcess Chudnovsky ... 30,000,000 iterations and 274.18 seconds.
[DEBUG] 2022-10-03 09:29:47,075 __bs: MainProcess Chudnovsky ... 31,000,000 iterations and 286.53 seconds.
[DEBUG] 2022-10-03 09:29:53,746 __bs: MainProcess Chudnovsky ... 32,000,000 iterations and 293.20 seconds.
[DEBUG] 2022-10-03 09:29:59,099 __bs: MainProcess Chudnovsky ... 33,000,000 iterations and 298.56 seconds.
[DEBUG] 2022-10-03 09:30:07,511 __bs: MainProcess Chudnovsky ... 34,000,000 iterations and 306.97 seconds.
[DEBUG] 2022-10-03 09:30:14,279 __bs: MainProcess Chudnovsky ... 35,000,000 iterations and 313.74 seconds.
[DEBUG] 2022-10-03 09:31:31,710 __bs: MainProcess Chudnovsky ... 36,000,000 iterations and 391.17 seconds.
[DEBUG] 2022-10-03 09:31:38,454 __bs: MainProcess Chudnovsky ... 37,000,000 iterations and 397.91 seconds.
[DEBUG] 2022-10-03 09:31:46,437 __bs: MainProcess Chudnovsky ... 38,000,000 iterations and 405.89 seconds.
[DEBUG] 2022-10-03 09:31:53,285 __bs: MainProcess Chudnovsky ... 39,000,000 iterations and 412.74 seconds.
[DEBUG] 2022-10-03 09:32:05,602 __bs: MainProcess Chudnovsky ... 40,000,000 iterations and 425.06 seconds.
[DEBUG] 2022-10-03 09:32:12,220 __bs: MainProcess Chudnovsky ... 41,000,000 iterations and 431.68 seconds.
[DEBUG] 2022-10-03 09:32:20,708 __bs: MainProcess Chudnovsky ... 42,000,000 iterations and 440.17 seconds.
[DEBUG] 2022-10-03 09:32:27,552 __bs: MainProcess Chudnovsky ... 43,000,000 iterations and 447.01 seconds.
[DEBUG] 2022-10-03 09:32:32,986 __bs: MainProcess Chudnovsky ... 44,000,000 iterations and 452.44 seconds.
[DEBUG] 2022-10-03 09:32:53,904 __bs: MainProcess Chudnovsky ... 45,000,000 iterations and 473.36 seconds.
[DEBUG] 2022-10-03 09:33:00,832 __bs: MainProcess Chudnovsky ... 46,000,000 iterations and 480.29 seconds.
[DEBUG] 2022-10-03 09:33:09,198 __bs: MainProcess Chudnovsky ... 47,000,000 iterations and 488.66 seconds.
[DEBUG] 2022-10-03 09:33:16,000 __bs: MainProcess Chudnovsky ... 48,000,000 iterations and 495.46 seconds.
[DEBUG] 2022-10-03 09:33:27,921 __bs: MainProcess Chudnovsky ... 49,000,000 iterations and 507.38 seconds.
[DEBUG] 2022-10-03 09:33:34,778 __bs: MainProcess Chudnovsky ... 50,000,000 iterations and 514.24 seconds.
[DEBUG] 2022-10-03 09:33:43,298 __bs: MainProcess Chudnovsky ... 51,000,000 iterations and 522.76 seconds.
[DEBUG] 2022-10-03 09:33:49,959 __bs: MainProcess Chudnovsky ... 52,000,000 iterations and 529.42 seconds.
[DEBUG] 2022-10-03 09:34:29,294 __bs: MainProcess Chudnovsky ... 53,000,000 iterations and 568.75 seconds.
[DEBUG] 2022-10-03 09:34:36,176 __bs: MainProcess Chudnovsky ... 54,000,000 iterations and 575.63 seconds.
[DEBUG] 2022-10-03 09:34:41,576 __bs: MainProcess Chudnovsky ... 55,000,000 iterations and 581.03 seconds.
[DEBUG] 2022-10-03 09:34:50,161 __bs: MainProcess Chudnovsky ... 56,000,000 iterations and 589.62 seconds.
[DEBUG] 2022-10-03 09:34:56,811 __bs: MainProcess Chudnovsky ... 57,000,000 iterations and 596.27 seconds.
[DEBUG] 2022-10-03 09:35:09,382 __bs: MainProcess Chudnovsky ... 58,000,000 iterations and 608.84 seconds.
[DEBUG] 2022-10-03 09:35:16,206 __bs: MainProcess Chudnovsky ... 59,000,000 iterations and 615.66 seconds.
[DEBUG] 2022-10-03 09:35:24,295 __bs: MainProcess Chudnovsky ... 60,000,000 iterations and 623.75 seconds.
[DEBUG] 2022-10-03 09:35:31,095 __bs: MainProcess Chudnovsky ... 61,000,000 iterations and 630.55 seconds.
[DEBUG] 2022-10-03 09:35:52,139 __bs: MainProcess Chudnovsky ... 62,000,000 iterations and 651.60 seconds.
[DEBUG] 2022-10-03 09:35:58,781 __bs: MainProcess Chudnovsky ... 63,000,000 iterations and 658.24 seconds.
[DEBUG] 2022-10-03 09:36:07,399 __bs: MainProcess Chudnovsky ... 64,000,000 iterations and 666.86 seconds.
[DEBUG] 2022-10-03 09:36:12,847 __bs: MainProcess Chudnovsky ... 65,000,000 iterations and 672.30 seconds.
[DEBUG] 2022-10-03 09:36:19,763 __bs: MainProcess Chudnovsky ... 66,000,000 iterations and 679.22 seconds.
[DEBUG] 2022-10-03 09:36:32,351 __bs: MainProcess Chudnovsky ... 67,000,000 iterations and 691.81 seconds.
[DEBUG] 2022-10-03 09:36:39,078 __bs: MainProcess Chudnovsky ... 68,000,000 iterations and 698.53 seconds.
[DEBUG] 2022-10-03 09:36:47,830 __bs: MainProcess Chudnovsky ... 69,000,000 iterations and 707.29 seconds.
[DEBUG] 2022-10-03 09:36:54,701 __bs: MainProcess Chudnovsky ... 70,000,000 iterations and 714.16 seconds.
[DEBUG] 2022-10-03 09:39:39,357 __bs: MainProcess Chudnovsky ... 71,000,000 iterations and 878.81 seconds.
[DEBUG] 2022-10-03 09:39:46,199 __bs: MainProcess Chudnovsky ... 72,000,000 iterations and 885.66 seconds.
[DEBUG] 2022-10-03 09:39:54,956 __bs: MainProcess Chudnovsky ... 73,000,000 iterations and 894.41 seconds.
[DEBUG] 2022-10-03 09:40:01,639 __bs: MainProcess Chudnovsky ... 74,000,000 iterations and 901.10 seconds.
[DEBUG] 2022-10-03 09:40:14,219 __bs: MainProcess Chudnovsky ... 75,000,000 iterations and 913.68 seconds.
[DEBUG] 2022-10-03 09:40:19,680 __bs: MainProcess Chudnovsky ... 76,000,000 iterations and 919.14 seconds.
[DEBUG] 2022-10-03 09:40:26,625 __bs: MainProcess Chudnovsky ... 77,000,000 iterations and 926.08 seconds.
[DEBUG] 2022-10-03 09:40:35,212 __bs: MainProcess Chudnovsky ... 78,000,000 iterations and 934.67 seconds.
[DEBUG] 2022-10-03 09:40:41,914 __bs: MainProcess Chudnovsky ... 79,000,000 iterations and 941.37 seconds.
[DEBUG] 2022-10-03 09:41:03,218 __bs: MainProcess Chudnovsky ... 80,000,000 iterations and 962.68 seconds.
[DEBUG] 2022-10-03 09:41:10,213 __bs: MainProcess Chudnovsky ... 81,000,000 iterations and 969.67 seconds.
[DEBUG] 2022-10-03 09:41:18,344 __bs: MainProcess Chudnovsky ... 82,000,000 iterations and 977.80 seconds.
[DEBUG] 2022-10-03 09:41:25,261 __bs: MainProcess Chudnovsky ... 83,000,000 iterations and 984.72 seconds.
[DEBUG] 2022-10-03 09:41:37,663 __bs: MainProcess Chudnovsky ... 84,000,000 iterations and 997.12 seconds.
[DEBUG] 2022-10-03 09:41:44,680 __bs: MainProcess Chudnovsky ... 85,000,000 iterations and 1004.14 seconds.
[DEBUG] 2022-10-03 09:41:53,411 __bs: MainProcess Chudnovsky ... 86,000,000 iterations and 1012.87 seconds.
[DEBUG] 2022-10-03 09:41:58,926 __bs: MainProcess Chudnovsky ... 87,000,000 iterations and 1018.38 seconds.
[DEBUG] 2022-10-03 09:42:05,858 __bs: MainProcess Chudnovsky ... 88,000,000 iterations and 1025.32 seconds.
[DEBUG] 2022-10-03 09:42:46,163 __bs: MainProcess Chudnovsky ... 89,000,000 iterations and 1065.62 seconds.
[DEBUG] 2022-10-03 09:42:53,054 __bs: MainProcess Chudnovsky ... 90,000,000 iterations and 1072.51 seconds.
[DEBUG] 2022-10-03 09:43:02,030 __bs: MainProcess Chudnovsky ... 91,000,000 iterations and 1081.49 seconds.
[DEBUG] 2022-10-03 09:43:09,192 __bs: MainProcess Chudnovsky ... 92,000,000 iterations and 1088.65 seconds.
[DEBUG] 2022-10-03 09:43:21,533 __bs: MainProcess Chudnovsky ... 93,000,000 iterations and 1100.99 seconds.
[DEBUG] 2022-10-03 09:43:28,643 __bs: MainProcess Chudnovsky ... 94,000,000 iterations and 1108.10 seconds.
[DEBUG] 2022-10-03 09:43:37,372 __bs: MainProcess Chudnovsky ... 95,000,000 iterations and 1116.83 seconds.
[DEBUG] 2022-10-03 09:43:44,558 __bs: MainProcess Chudnovsky ... 96,000,000 iterations and 1124.02 seconds.
[DEBUG] 2022-10-03 09:44:06,555 __bs: MainProcess Chudnovsky ... 97,000,000 iterations and 1146.01 seconds.
[DEBUG] 2022-10-03 09:44:12,220 __bs: MainProcess Chudnovsky ... 98,000,000 iterations and 1151.68 seconds.
[DEBUG] 2022-10-03 09:44:19,278 __bs: MainProcess Chudnovsky ... 99,000,000 iterations and 1158.74 seconds.
[DEBUG] 2022-10-03 09:44:28,323 __bs: MainProcess Chudnovsky ... 100,000,000 iterations and 1167.78 seconds.
[DEBUG] 2022-10-03 09:44:35,211 __bs: MainProcess Chudnovsky ... 101,000,000 iterations and 1174.67 seconds.
[DEBUG] 2022-10-03 09:44:48,331 __bs: MainProcess Chudnovsky ... 102,000,000 iterations and 1187.79 seconds.
[DEBUG] 2022-10-03 09:44:54,835 __bs: MainProcess Chudnovsky ... 103,000,000 iterations and 1194.29 seconds.
[DEBUG] 2022-10-03 09:45:03,869 __bs: MainProcess Chudnovsky ... 104,000,000 iterations and 1203.33 seconds.
[DEBUG] 2022-10-03 09:45:10,967 __bs: MainProcess Chudnovsky ... 105,000,000 iterations and 1210.42 seconds.
[DEBUG] 2022-10-03 09:46:32,760 __bs: MainProcess Chudnovsky ... 106,000,000 iterations and 1292.22 seconds.
[DEBUG] 2022-10-03 09:46:39,872 __bs: MainProcess Chudnovsky ... 107,000,000 iterations and 1299.33 seconds.
[DEBUG] 2022-10-03 09:46:48,948 __bs: MainProcess Chudnovsky ... 108,000,000 iterations and 1308.41 seconds.
[DEBUG] 2022-10-03 09:46:54,611 __bs: MainProcess Chudnovsky ... 109,000,000 iterations and 1314.07 seconds.
[DEBUG] 2022-10-03 09:47:01,727 __bs: MainProcess Chudnovsky ... 110,000,000 iterations and 1321.18 seconds.
[DEBUG] 2022-10-03 09:47:14,525 __bs: MainProcess Chudnovsky ... 111,000,000 iterations and 1333.98 seconds.
[DEBUG] 2022-10-03 09:47:21,682 __bs: MainProcess Chudnovsky ... 112,000,000 iterations and 1341.14 seconds.
[DEBUG] 2022-10-03 09:47:30,610 __bs: MainProcess Chudnovsky ... 113,000,000 iterations and 1350.07 seconds.
[DEBUG] 2022-10-03 09:47:37,176 __bs: MainProcess Chudnovsky ... 114,000,000 iterations and 1356.63 seconds.
[DEBUG] 2022-10-03 09:47:59,642 __bs: MainProcess Chudnovsky ... 115,000,000 iterations and 1379.10 seconds.
[DEBUG] 2022-10-03 09:48:06,702 __bs: MainProcess Chudnovsky ... 116,000,000 iterations and 1386.16 seconds.
[DEBUG] 2022-10-03 09:48:15,483 __bs: MainProcess Chudnovsky ... 117,000,000 iterations and 1394.94 seconds.
[DEBUG] 2022-10-03 09:48:22,537 __bs: MainProcess Chudnovsky ... 118,000,000 iterations and 1401.99 seconds.
[DEBUG] 2022-10-03 09:48:35,714 __bs: MainProcess Chudnovsky ... 119,000,000 iterations and 1415.17 seconds.
[DEBUG] 2022-10-03 09:48:41,321 __bs: MainProcess Chudnovsky ... 120,000,000 iterations and 1420.78 seconds.
[DEBUG] 2022-10-03 09:48:48,408 __bs: MainProcess Chudnovsky ... 121,000,000 iterations and 1427.87 seconds.
[DEBUG] 2022-10-03 09:48:57,138 __bs: MainProcess Chudnovsky ... 122,000,000 iterations and 1436.60 seconds.
[DEBUG] 2022-10-03 09:49:04,328 __bs: MainProcess Chudnovsky ... 123,000,000 iterations and 1443.79 seconds.
[DEBUG] 2022-10-03 09:49:46,274 __bs: MainProcess Chudnovsky ... 124,000,000 iterations and 1485.73 seconds.
[DEBUG] 2022-10-03 09:49:52,833 __bs: MainProcess Chudnovsky ... 125,000,000 iterations and 1492.29 seconds.
[DEBUG] 2022-10-03 09:50:01,786 __bs: MainProcess Chudnovsky ... 126,000,000 iterations and 1501.24 seconds.
[DEBUG] 2022-10-03 09:50:08,975 __bs: MainProcess Chudnovsky ... 127,000,000 iterations and 1508.43 seconds.
[DEBUG] 2022-10-03 09:50:21,850 __bs: MainProcess Chudnovsky ... 128,000,000 iterations and 1521.31 seconds.
[DEBUG] 2022-10-03 09:50:28,962 __bs: MainProcess Chudnovsky ... 129,000,000 iterations and 1528.42 seconds.
[DEBUG] 2022-10-03 09:50:34,594 __bs: MainProcess Chudnovsky ... 130,000,000 iterations and 1534.05 seconds.
[DEBUG] 2022-10-03 09:50:43,647 __bs: MainProcess Chudnovsky ... 131,000,000 iterations and 1543.10 seconds.
[DEBUG] 2022-10-03 09:50:50,724 __bs: MainProcess Chudnovsky ... 132,000,000 iterations and 1550.18 seconds.
[DEBUG] 2022-10-03 09:51:12,742 __bs: MainProcess Chudnovsky ... 133,000,000 iterations and 1572.20 seconds.
[DEBUG] 2022-10-03 09:51:19,799 __bs: MainProcess Chudnovsky ... 134,000,000 iterations and 1579.26 seconds.
[DEBUG] 2022-10-03 09:51:28,824 __bs: MainProcess Chudnovsky ... 135,000,000 iterations and 1588.28 seconds.
[DEBUG] 2022-10-03 09:51:35,324 __bs: MainProcess Chudnovsky ... 136,000,000 iterations and 1594.78 seconds.
[DEBUG] 2022-10-03 09:51:48,419 __bs: MainProcess Chudnovsky ... 137,000,000 iterations and 1607.88 seconds.
[DEBUG] 2022-10-03 09:51:55,634 __bs: MainProcess Chudnovsky ... 138,000,000 iterations and 1615.09 seconds.
[DEBUG] 2022-10-03 09:52:04,435 __bs: MainProcess Chudnovsky ... 139,000,000 iterations and 1623.89 seconds.
[DEBUG] 2022-10-03 09:52:11,583 __bs: MainProcess Chudnovsky ... 140,000,000 iterations and 1631.04 seconds.
[DEBUG] 2022-10-03 09:52:17,222 __bs: MainProcess Chudnovsky ... 141,000,000 iterations and 1636.68 seconds.
[DEBUG] 2022-10-03 10:02:43,939 compute: MainProcess Chudnovsky brothers 1988
π = (Q(0, N) / 12T(0, N) + 12AQ(0, N))**(C**(3/2))
calulation Done! 141,027,339 iterations and 2263.39 seconds.
[INFO] 2022-10-03 10:09:07,119 <module>: MainProcess Last 5 digits of π were 45519 as expected at offset 999,999,995
[INFO] 2022-10-03 10:09:07,119 <module>: MainProcess Calculated π to 1,000,000,000 digits using a formula of:
10 Chudnovsky brothers 1988
π = (Q(0, N) / 12T(0, N) + 12AQ(0, N))**(C**(3/2))
[INFO] 2022-10-03 10:09:07,120 <module>: MainProcess Calculation took 141,027,339 iterations and 0:44:06.398345.
math_pi.pi(b = 1000000) быстрее до миллиона. Примерно в 40 раз быстрее. Но до миллиарда не дойдет. 1 миллион - это наибольшее количество цифр.
Встроенный GMPY выглядит так:
python pi-pourri.py -v -d 1,000,000,000 -a 11
[INFO] 2022-10-03 14:33:34,729 <module>: MainProcess Computing π to 1,000,000,000 digits.
[DEBUG] 2022-10-03 14:33:34,729 compute: MainProcess Starting const_pi() function from the gmpy2 library formula to 1,000,000,000 decimal places
[DEBUG] 2022-10-03 15:46:46,575 compute: MainProcess const_pi() function from the gmpy2 library calulation Done! 1 iterations and 4391.85 seconds.
[INFO] 2022-10-03 15:46:46,575 <module>: MainProcess Last 5 digits of π were 45519 as expected at offset 999,999,995
[INFO] 2022-10-03 15:46:46,575 <module>: MainProcess Calculated π to 1,000,000,000 digits using a formula of:
11 const_pi() function from the gmpy2 library
[INFO] 2022-10-03 15:46:46,575 <module>: MainProcess Calculation took 1 iterations and 1:13:11.845652.
Встроенный MPmath работает почти так же быстро. Примерно на 12% (6 минут) медленнее:
python pi-pourri.py -v -a 12 -d 1,000,000,000
[INFO] 2022-10-04 09:10:37,085 <module>: MainProcess Computing π to 1,000,000,000 digits.
[DEBUG] 2022-10-04 09:10:37,085 compute: MainProcess Starting mp.pi() function from the mpmath library formula to 1,000,000,000 decimal places
[DEBUG] 2022-10-04 10:01:25,321 compute: MainProcess mp.pi() function from the mpmath library calulation Done! 1 iterations and 3048.22 seconds.
[INFO] 2022-10-04 10:01:25,338 <module>: MainProcess Last 5 digits of π were 45519 as expected at offset 999,999,995
[INFO] 2022-10-04 10:01:25,340 <module>: MainProcess Calculated π to 1,000,000,000 digits using a formula of:
12 mp.pi() function from the mpmath library
[INFO] 2022-10-04 10:01:25,343 <module>: MainProcess Calculation took 1 iterations and 0:50:48.250337.
Лучший подход
Чтобы получить выходные данные стандартных констант, таких как pi или стандартные понятия, мы должны сначала использовать встроенные методы, доступные на языке, который вы используете. Он вернет значение самым быстрым и лучшим способом. Я использую Python, чтобы получить самый быстрый способ получить значение пи
- Пи переменная математической библиотеки. В библиотеке Math переменная pi хранится как константа.
math_pi.py
import math
print math.pi
Запустите скрипт с утилитой времени linux /usr/bin/time -v python math_pi.py
Выход:
Command being timed: "python math_pi.py"
User time (seconds): 0.01
System time (seconds): 0.01
Percent of CPU this job got: 91%
Elapsed (wall clock) time (h:mm:ss or m:ss): 0:00.03
- Используйте метод аркос, потому что математика
acos_pi.py
import math
print math.acos(-1)
Запустите скрипт с утилитой времени linux /usr/bin/time -v python acos_pi.py
Выход:
Command being timed: "python acos_pi.py"
User time (seconds): 0.02
System time (seconds): 0.01
Percent of CPU this job got: 94%
Elapsed (wall clock) time (h:mm:ss or m:ss): 0:00.03
- использовать формулу BBP
bbp_pi.py
from decimal import Decimal, getcontext
getcontext().prec=100
print sum(1/Decimal(16)**k *
(Decimal(4)/(8*k+1) -
Decimal(2)/(8*k+4) -
Decimal(1)/(8*k+5) -
Decimal(1)/(8*k+6)) for k in range(100))
Запустите скрипт с утилитой времени linux /usr/bin/time -v python bbp_pi.py
Выход:
Command being timed: "python c.py"
User time (seconds): 0.05
System time (seconds): 0.01
Percent of CPU this job got: 98%
Elapsed (wall clock) time (h:mm:ss or m:ss): 0:00.06
Поэтому лучше всего использовать встроенный метод, предоставляемый языком, потому что он самый быстрый и лучший для получения результата. В питоне используйте math.pi