Разложение в выпуклые полигоны
Этот вопрос немного запутан. Я написал алгоритм разбиения простого многоугольника на выпуклые подполигоны, но теперь у меня возникают проблемы с доказательством того, что он не оптимален (т. Е. Минимальное количество выпуклых многоугольников с использованием точек Штейнера (добавленные вершины)). Мой профессор непреклонен, что это не может быть сделано с жадным алгоритмом, таким как этот, но я не могу придумать контрпример.
Итак, если кто-то может доказать, что мой алгоритм неоптимален (или оптимален), я был бы признателен за это.
Самый простой способ объяснить мой алгоритм с помощью картинок (это из более старой неоптимальной версии)
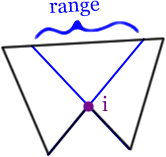
Что мой алгоритм делает, так это расширяет отрезки линии вокруг точки, через которую я попадаю, пока не достигнет точки на противоположном краю.
Если в этом диапазоне нет вершины, она создает новую (красную точку) и соединяется с ней:
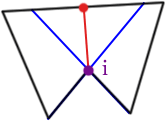
Если в диапазоне есть одна или несколько вершин, он соединяется с ближайшей. Обычно это приводит к разложению с наименьшим числом выпуклых многоугольников:
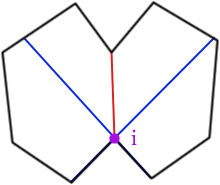
Однако в некоторых случаях это может привести к сбою - на следующем рисунке, если случится сначала соединить среднюю зеленую линию, это создаст лишний ненужный многоугольник. Для этого я предлагаю дважды проверить все ребра (диагонали), которые мы добавили, и убедиться, что они все еще необходимы. Если нет, удалите его:
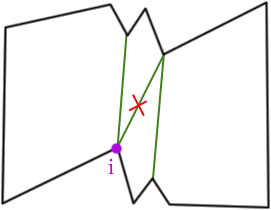
Однако в некоторых случаях этого недостаточно. Смотрите этот рисунок:
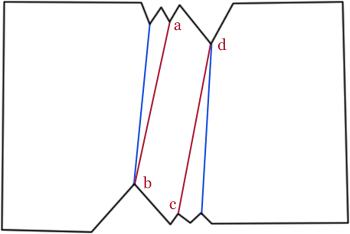
Замена ab и cd на ac даст лучшее решение. В этом сценарии, однако, нет ребер для удаления, поэтому это создает проблему. В этом случае я предлагаю порядок предпочтения: при решении, к какой вершине подключить рефлекторную вершину, она должна выбрать вершину с наивысшим приоритетом:
самая низкая) ближайшая вершина
мед) ближайшая рефлекторная вершина
самый высокий) самый близкий рефлекс, который также находится в диапазоне при работе в обратном направлении (трудно объяснить) -
На этом рисунке мы видим, что рефлекторная вершина 9 решила соединиться с 12 (потому что она была ближе всего), когда было бы лучше соединиться с 5. Обе вершины 5 и 12 находятся в диапазоне, как определено расширенной линией. сегменты 10-9 и 8-9, но вершине 5 следует отдавать предпочтение, потому что 9 находится в пределах диапазона, заданного 4-5 и 6-5, но НЕ в диапазоне, заданном 13-12 и 11-12. то есть, ребро 9-12 облегчает вершину рефлекса в 9, но НЕ удаляет вершину рефлекса в 12, но МОЖЕТ устранить вершину рефлекса в 5, поэтому 5 следует отдавать предпочтение.
Возможно, что край 5-12 все еще будет существовать с этой модифицированной версией, но он может быть удален во время последующей обработки.
Есть ли случаи, которые я пропустил?
Псевдокод (запрошенный Джоном Феминеллой) - в нем отсутствуют биты на рисунках 3 и 5
assume vertices in `poly` are given in CCW order
let 'good reflex' (better term??) mean that if poly[i] is being compared with poly[j], then poly[i] is in the range given by the rays poly[j-1], poly[j] and poly[j+1], poly[j]
for each vertex poly[i]
if poly[i] is reflex
find the closest point of intersection given by the ray starting at poly[i-1] and extending in the direction of poly[i] (call this lower bound)
repeat for the ray given by poly[i+1], poly[i] (call this upper bound)
if there are no vertices along boundary of the polygon in the range given by the upper and lower bounds
create a new vertex exactly half way between the lower and upper bound points (lower and upper will lie on the same edge)
connect poly[i] to this new point
else
iterate along the vertices in the range given by the lower and upper bounds, for each vertex poly[j]
if poly[j] is a 'good reflex'
if no other good reflexes have been found
save it (overwrite any other vertex found)
else
if it is closer then the other good reflexes vertices, save it
else
if no good reflexes have been found and it is closer than the other vertices found, save it
connect poly[i] to the best candidate
repeat entire algorithm for both halves of the polygon that was just split
// no reflex vertices found, then `poly` is convex
save poly
Оказывается, есть еще один случай, которого я не ожидал: [Рисунок 5]
Мой алгоритм попытается соединить вершины с 1 по 4, если я не добавлю еще одну проверку, чтобы убедиться, что это возможно. Поэтому я предлагаю поместить все "в диапазоне" в очередь с приоритетами, используя схему приоритетов, о которой я упоминал выше, затем взять наивысшую приоритетную, проверить, может ли она подключиться, если нет, вынуть ее и использовать следующую. Я думаю, что это делает мой алгоритм O(r n log n), если я правильно его оптимизирую.
Я собрал веб-сайт, который свободно описывает мои выводы. Я склонен что-то передвигать, так что бери, пока жарко.
4 ответа
Я считаю, что правильная пятиконечная звезда (например, с чередующимися точками, имеющими коллинеарные сегменты) является контрпримером, который вы ищете.
Редактировать в ответ на комментарии
В свете моего пересмотренного понимания, пересмотренный ответ: попробуйте острую пятиконечную звезду (например, ту, у которой руки достаточно узкие, так что только три точки, составляющие руку напротив точки рефлекса, над которой вы работаете, находятся в диапазоне, который считается "точками хорошего отражения").). По крайней мере, работая с ним на бумаге, он дает больше, чем оптимальный. Однако, окончательное чтение вашего кода заставляет меня задуматься: что вы подразумеваете под "самым близким" (то есть самым близким к чему)?
Заметка
Хотя мой ответ был принят, это не контрпример, который мы изначально думали. Как отмечает @Mark в комментариях, оно увеличивается с четырех до пяти в одно и то же время, что и оптимальное.
Триггер, триггер
Если подумать дальше, думаю, я был прав. Оптимальную границу четырех можно сохранить в острой звезде, просто убедившись, что одна пара рук имеет коллинеарные ребра. Но алгоритм находит пять, даже с исправлением.
Я получаю это:
удаление мертвой ссылки ImageShack
Когда оптимально это:
удаление мертвой ссылки ImageShack
Я думаю, что ваш алгоритм не может быть оптимальным, потому что он не использует никакой меры оптимальности. Вы используете другие метрики, такие как "ближайшие" вершины, и проверяете наличие "необходимых" диагоналей.
Чтобы вбить клин между вашим и оптимальным алгоритмом, нам нужно использовать этот разрыв, ища фигуры с близкими вершинами, которые плохо разлагаются. Например (игнорируйте строки, я нашел это в intertubenet):
http://avocado-cad.wiki.sourceforge.net/space/showimage/2007-03-19_-_convexize.png
У вас нет защиты от того, что центральная точка соединяется через вогнутый "зазор", который является внешним по отношению к многоугольнику.
Ваш алгоритм также довольно сложен, и, возможно, переусердствует с ним - точно так же, как сложный код, вы можете найти в нем ошибки, потому что сложный код делает сложные предположения.
Рассмотрим более обширную начальную стадию, чтобы разбить фигуру на более простые фигуры, такие как треугольники, а затем итеративный или генетический алгоритм для их рекомбинации. Вам понадобится такая стадия, чтобы объединить любые ненужные деления между вашими выпуклыми полисами в любом случае, и к тому времени вы, возможно, ограничите свои возможные разложения только неоптимальными решениями.
На предположение что-то вроде:
- разложить на треугольники
- недетерминированно генерировать ряд рекомбинаций
- рассчитать метрику качества (количество полисов)
- выберите лучший x% рекомбинаций
- частично разложить каждый, используя треугольники, и генерировать новый набор рекомбинаций
- повторите с 4 до некоторой степени сходимости
Как насчет этого? http://img24.imageshack.us/img24/2994/picture2uvf.png
но вершина 5 должна быть отдана предпочтение, потому что 9 находится в диапазоне, указанном 4-5 и 6-5
Что бы вы сделали, если бы 4-5 и 6-5 были еще более выпуклыми, чтобы 9 не лежало в пределах их диапазона? Тогда, по вашим правилам, правильнее всего было бы соединить 9–12, потому что 12 - ближайшая рефлекторная вершина, которая была бы неоптимальной.
Нашел это:(Они на самом деле довольно очевидны.
* Dead Imageshack IMG *
Четырехлистный клевер не будет оптимальным, если разрешены точки Штейнера... красные вершины могли быть связаны.
* Dead Imageshack IMG *
Это даже не будет оптимальным без очков Штейнера... 5 можно подключить к 14, избавляя от необходимости 3-14, 3-12 и 5-12. Это могло бы быть на два полигона лучше! Ой!