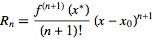Реализация Sine в Java без функции Math.sin

Question

Я пытаюсь реализовать функцию синуса в Java без использования Math.sin(x), Поэтому я пытаюсь понять это с помощью серии Тейлора. К сожалению, этот код дает неправильный результат (ы).

Если вы не знаете, что такое серия Тейлор, посмотрите:

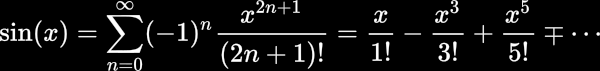
Вот фрагмент кода, который я создал:

public static double sin(double a) {
   double temp = 1;
   int denominator = -1;
   if(a == Double.NEGATIVE_INFINITY || !(a < Double.POSITIVE_INFINITY)) {
      return Double.NaN;
   } 
   if(a != 0) {
      for (int i = 0; i <= a; i++) {
         denominator += 2;
         if(i % 2 == 0) {
            temp = temp + (Math.pow(a, denominator) / Factorial.factorial(denominator));
         } else {
            temp = temp - (Math.pow(a, denominator) / Factorial.factorial(denominator));
         }
      }
   }
   return temp;
}

Я не могу найти ошибку, которую я сделал. Вы?

Answer 1

В вашем коде есть две основные проблемы. Первая проблема заключается в том, что вы цикл i от 0 в a, Это означает, что если a является отрицательным значением, for цикл даже не запускается и ваш результат всегда будет 1.0, Тогда как если a положительно, цикл запускается, но останавливается после (int) a итерации, и это не имеет особого смысла, так как аппроксимация Тейлора прекрасно работает, когда итерации n стремятся к бесконечности.

Вторая важная проблема заключается в том, что вы недостаточно контролируете входное значение. a, Как я уже говорил в Python: вычислить синус / косинус с точностью до 1 миллиона цифр

Реальное разложение Тейлора с центром в x ₀:

где Rn - остаток Лагранжа

Обратите внимание, что Rn быстро растет, как только x удаляется от центра x0.

Поскольку вы реализуете серию Маклаурина (ряд Тейлора с центром в 0), а не общую серию Тейлора, ваша функция даст действительно неверные результаты при попытке вычислить sin(x) для больших значений x.

Так что до for В цикле вы должны уменьшить домен по крайней мере до [-pi, pi]... лучше, если вы уменьшите его до [0, pi] и воспользуетесь четностью синуса.

Рабочий код:

public static double sin(double a) {

    if (a == Double.NEGATIVE_INFINITY || !(a < Double.POSITIVE_INFINITY)) {
        return Double.NaN;
    }

    // If you can't use Math.PI neither,
    // you'll have to create your own PI
    final double PI = 3.14159265358979323846;

    // Fix the domain for a...

    // Sine is a periodic function with period = 2*PI
    a %= 2 * PI;
    // Any negative angle can be brought back
    // to it's equivalent positive angle
    if (a < 0) {
        a = 2 * PI - a;
    }
    // Also sine is an odd function...
    // let's take advantage of it.
    int sign = 1;
    if (a > PI) {
        a -= PI;
        sign = -1;
    }
    // Now a is in range [0, pi].


    // Calculate sin(a)

    // Set precision to fit your needs.
    // Note that 171! > Double.MAX_VALUE, so
    // don't set PRECISION to anything greater
    // than 84 unless you are sure your
    // Factorial.factorial() can handle it
    final int PRECISION = 50;
    double temp = 0;
    for (int i = 0; i <= PRECISION; i++) {
        temp += Math.pow(-1, i) * (Math.pow(a, 2 * i + 1) / Factorial.factorial(2 * i + 1));
    }

    return sign * temp;

}

Answer 2

Ваша проблема заключается в том, что вы используете значение, которое должно оцениваться для функции синуса, в качестве предела для знаменателя. Ряд Тейлора оценивается, когда предел функции приближается к бесконечности. В этом случае вы оцениваете его только по размеру входного значения, что на самом деле не имеет смысла. Вы должны заменить свой for сравнение петель с i < x где x - это константа, представляющая, какую бы точность вы ни хотели сделать (функция будет достаточно точной для значения, равного 20 или около того).