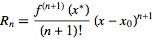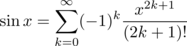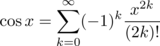Python: вычислить синус / косинус с точностью до 1 миллиона цифр

Question

Вопрос довольно понятен. Я видел пару примеров для pi, но не для функций trigo. Возможно, можно использовать серию Тейлора, как здесь, но я не совсем уверен, как реализовать это в python. Особенно, как хранить так много цифр. Я должен упомянуть: в идеале это будет работать на vanilla python, т.е.

Спасибо!

Редактировать: как я уже сказал, я знаю, что вопрос задавался ранее, но это на Java, и я искал реализацию Python:)

Редактировать 2: вау, я не знал, что люди здесь могут быть настолько погружены в себя. Я попробовал несколько подходов, но ни один из них не сработал. Я думал, что это место, куда вы можете обратиться за советом, думаю, я ошибся

Последнее редактирование: Для тех, кто может найти это полезным: многие углы могут быть рассчитаны как кратные sqrt(2), sqrt(3) и Phi (1.61803..), поскольку эти числа широко доступны с точностью до 10 миллионов цифр, полезно иметь их в файле и читать их в вашей программе напрямую

Answer 1

mpmath это путь:

from mpmath import mp
precision = 1000000
mp.dps = precision
mp.cos(0.1)

---

Если вы не можете установить mpmath или любой другой модуль, вы можете попробовать полиномиальное приближение, как предложено.

где Rn - остаток Лагранжа

Обратите внимание, что Rn быстро растет, как только x удаляется от центра x₀, поэтому будьте осторожны, используя ряд Маклаурина (ряд Тейлора с центром в 0) при попытке вычислить sin(x) или cos(x) произвольного x.

Answer 2

Попробуй это

import math
from decimal import *


def sin_taylor(x, decimals):
    p = 0
    getcontext().prec = decimals
    for n in range(decimals):
        p += Decimal(((-1)**n)*(x**(2*n+1)))/(Decimal(math.factorial(2*n+1)))
    return p


def cos_taylor(x, decimals):
    p = 0
    getcontext().prec = decimals
    for n in range(decimals):
        p += Decimal(((-1)**n)*(x**(2*n)))/(Decimal(math.factorial(2*n)))
    return p

if __name__ == "__main__":
    ang = 0.1
    decimals = 1000000
    print 'sin:', sin_taylor(ang, decimals)
    print 'cos:', cos_taylor(ang, decimals)

Answer 3

import math
x = .5
def sin(x):
    sum = 0
    for a in range(0,50): #this number (50) to be changed for more accurate results
        sum+=(math.pow(-1,a))/(math.factorial(2*a+1))*(math.pow(x,2*a+1))
    return sum

ans = sin(x)
print(str.format('{0:.15f}', ans)) #change the 15 for more decimal places

Вот пример реализации ряда Тейлора с использованием Python, как вы предложили выше. После этого изменить не будет слишком сложно.

РЕДАКТИРОВАТЬ:

Добавлено в форматирование последней строки для фактической распечатки большего количества десятичных знаков.