Подгонка нормального распределения в R

Question

Я использую следующий код, чтобы соответствовать нормальному распределению. Ссылка для набора данных для "b" (слишком велика для прямой публикации):

ссылка для б

setwd("xxxxxx")
library(fitdistrplus)

require(MASS)
tazur <-read.csv("b", header= TRUE, sep=",")
claims<-tazur$b
a<-log(claims)
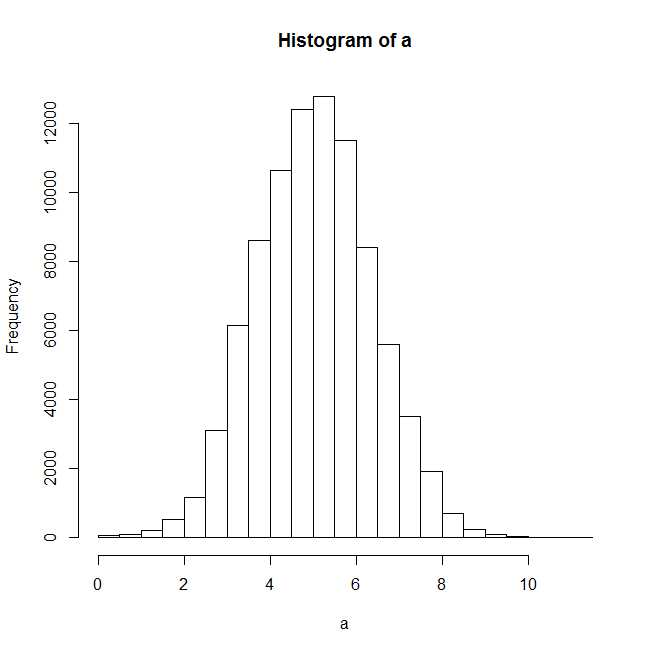
plot(hist(a))

После построения гистограммы нормальное распределение должно хорошо соответствовать.

f1n <- fitdistr(claims,"normal")
summary(f1n)

#Length Class  Mode   
#estimate 2      -none- numeric
#sd       2      -none- numeric
#vcov     4      -none- numeric
#n        1      -none- numeric
#loglik   1      -none- numeric

plot(f1n)

Ошибка в xy.coords (x, y, xlabel, ylabel, log):

"x" - это список, но не содержит компонентов "x" и "y"

Я получаю вышеуказанную ошибку, когда пытаюсь построить примерное распределение, и даже итоговая статистика отключена для f1n.

Буду признателен за любую помощь.

Answer 1

Похоже, вы путаете между MASS::fitdistr а также fitdistrplus::fitdist,

• MASS::fitdistr возвращает объект класса "fitdistr", и для этого нет метода заговора. Таким образом, вам нужно извлечь оценочные параметры и построить график предполагаемой плотности самостоятельно.
• Я не знаю почему вы грузите посылку fitdistrplusпотому что ваш вызов функции ясно показывает, что вы используете MASS, Тем не мение, fitdistrplus имеет функцию fitdist который возвращает объект класса "fitdist". Для этого класса есть метод plot, но он не будет работать для "fitdistr", возвращаемого MASS,

Я покажу вам, как работать с обоими пакетами.

## reproducible example
set.seed(0); x <- rnorm(500)

---

С помощьюMASS::fitdistr

Сюжетный метод недоступен, так что сделайте это сами.

library(MASS)
fit <- fitdistr(x, "normal")
class(fit)
# [1] "fitdistr"

para <- fit$estimate
#         mean            sd 
#-0.0002000485  0.9886248515 

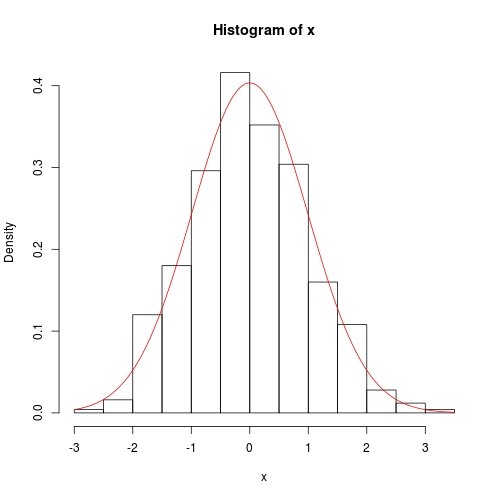
hist(x, prob = TRUE)
curve(dnorm(x, para[1], para[2]), col = 2, add = TRUE)

---

С помощьюfitdistrplus::fitdist

library(fitdistrplus)
FIT <- fitdist(x, "norm")    ## note: it is "norm" not "normal"
class(FIT)
# [1] "fitdist"

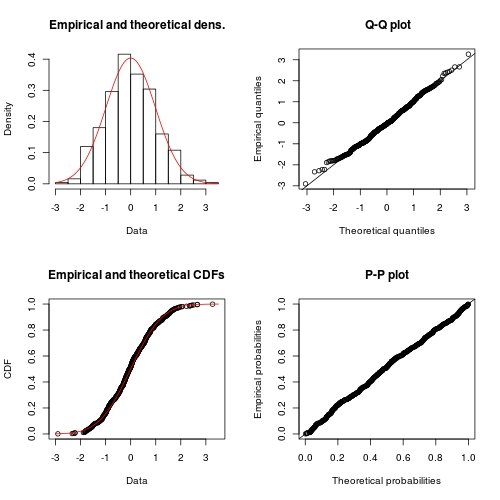
plot(FIT)    ## use method `plot.fitdist`

Answer 2

Обзор предыдущего ответа

В предыдущем ответе я не упомянул разницу между двумя методами. В общем, если мы выбираем максимальный вывод вероятности, я бы рекомендовал использовать MASS::fitdistrпотому что для многих основных распределений он выполняет точный вывод вместо численной оптимизации. Док о ?fitdistr сделал это довольно ясно:

For the Normal, log-Normal, geometric, exponential and Poisson
distributions the closed-form MLEs (and exact standard errors) are
used, and ‘start’ should not be supplied.

For all other distributions, direct optimization of the
log-likelihood is performed using ‘optim’.  The estimated standard
errors are taken from the observed information matrix, calculated
by a numerical approximation.  For one-dimensional problems the
Nelder-Mead method is used and for multi-dimensional problems the
BFGS method, unless arguments named ‘lower’ or ‘upper’ are
supplied (when ‘L-BFGS-B’ is used) or ‘method’ is supplied
explicitly.

С другой стороны, fitdistrplus::fitdist всегда выполняет вывод численным способом, даже если существует точный вывод. Конечно, преимущество fitdist является ли этот принцип более логическим выводом:

Fit of univariate distributions to non-censored data by maximum
likelihood (mle), moment matching (mme), quantile matching (qme)
or maximizing goodness-of-fit estimation (mge).

---

Цель этого ответа

Этот ответ собирается изучить точный вывод для нормального распределения. Это будет иметь теоретический характер, но нет доказательств принципа правдоподобия; даются только результаты. На основании этих результатов мы напишем нашу собственную R-функцию для точного вывода, которую можно сравнить с MASS::fitdistr, С другой стороны, сравнивать с fitdistrplus::fitdist, мы используем optim численно минимизировать отрицательную функцию логарифмического правдоподобия.

Это прекрасная возможность изучить статистику и сравнительно продвинутое использование optim, Для удобства оценю параметр масштаба: дисперсия, а не стандартная ошибка.

---

Точный вывод нормального распределения

---

Написание функции вывода сами

Следующий код хорошо прокомментирован. Есть переключатель exact, Если установлено FALSE, численное решение выбрано.

## fitting a normal distribution
fitnormal <- function (x, exact = TRUE) {
  if (exact) {
    ################################################
    ## Exact inference based on likelihood theory ##
    ################################################
    ## minimum negative log-likelihood (maximum log-likelihood) estimator of `mu` and `phi = sigma ^ 2`
    n <- length(x)
    mu <- sum(x) / n
    phi <- crossprod(x - mu)[1L] / n  # (a bised estimator, though)
    ## inverse of Fisher information matrix evaluated at MLE
    invI <- matrix(c(phi, 0, 0, phi * phi), 2L,
                   dimnames = list(c("mu", "sigma2"), c("mu", "sigma2")))
    ## log-likelihood at MLE
    loglik <- -(n / 2) * (log(2 * pi * phi) + 1)
    ## return
    return(list(theta = c(mu = mu, sigma2 = phi), vcov = invI, loglik = loglik, n = n))
    }
  else {
    ##################################################################
    ## Numerical optimization by minimizing negative log-likelihood ##
    ##################################################################
    ## negative log-likelihood function
    ## define `theta = c(mu, phi)` in order to use `optim`
    nllik <- function (theta, x) {
      (length(x) / 2) * log(2 * pi * theta[2]) + crossprod(x - theta[1])[1] / (2 * theta[2])
      }
    ## gradient function (remember to flip the sign when using partial derivative result of log-likelihood)
    ## define `theta = c(mu, phi)` in order to use `optim`
    gradient <- function (theta, x) {
      pl2pmu <- -sum(x - theta[1]) / theta[2]
      pl2pphi <- -crossprod(x - theta[1])[1] / (2 * theta[2] ^ 2) + length(x) / (2 * theta[2])
      c(pl2pmu, pl2pphi)
      }
    ## ask `optim` to return Hessian matrix by `hessian = TRUE`
    ## use "..." part to pass `x` as additional / further argument to "fn" and "gn"
    ## note, we want `phi` as positive so box constraint is used, with "L-BFGS-B" method chosen
    init <- c(sample(x, 1), sample(abs(x) + 0.1, 1))  ## arbitrary valid starting values
    z <- optim(par = init, fn = nllik, gr = gradient, x = x, lower = c(-Inf, 0), method = "L-BFGS-B", hessian = TRUE)
    ## post processing ##
    theta <- z$par
    loglik <- -z$value  ## flip the sign to get log-likelihood
    n <- length(x)
    ## Fisher information matrix (don't flip the sign as this is the Hessian for negative log-likelihood)
    I <- z$hessian / n  ## remember to take average to get mean
    invI <- solve(I, diag(2L))  ## numerical inverse
    dimnames(invI) <- list(c("mu", "sigma2"), c("mu", "sigma2"))
    ## return
    return(list(theta = theta, vcov = invI, loglik = loglik, n = n))
    }
  }

Мы все еще используем предыдущие данные для тестирования:

set.seed(0); x <- rnorm(500)

## exact inference
fit <- fitnormal(x)

#$theta
#           mu        sigma2 
#-0.0002000485  0.9773790969 
#
#$vcov
#              mu    sigma2
#mu     0.9773791 0.0000000
#sigma2 0.0000000 0.9552699
#
#$loglik
#[1] -703.7491
#
#$n
#[1] 500

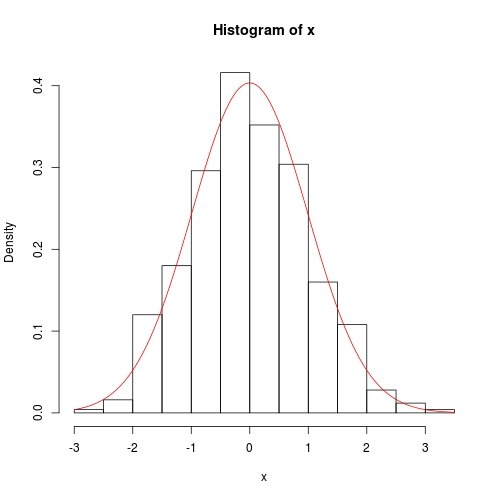
hist(x, prob = TRUE)
curve(dnorm(x, fit$theta[1], sqrt(fit$theta[2])), add = TRUE, col = 2)

Численный метод также довольно точен, за исключением того, что ковариация дисперсии не имеет точного 0 вне диагонали:

fitnormal(x, FALSE)

#$theta
#[1] -0.0002235315  0.9773732277
#
#$vcov
#                 mu       sigma2
#mu     9.773826e-01 5.359978e-06
#sigma2 5.359978e-06 1.910561e+00
#
#$loglik
#[1] -703.7491
#
#$n
#[1] 500