Как найти точку пересечения между прямой и прямоугольником?
У меня есть линия, которая идет от точек A до B; У меня есть (x,y) обеих точек. У меня также есть прямоугольник с центром в B и шириной и высотой прямоугольника.
Мне нужно найти точку в линии, которая пересекает прямоугольник. Есть ли формула, которая дает мне (x,y) этой точки?
14 ответов
/**
* Finds the intersection point between
* * the rectangle
* with parallel sides to the x and y axes
* * the half-line pointing towards (x,y)
* originating from the middle of the rectangle
*
* Note: the function works given min[XY] <= max[XY],
* even though minY may not be the "top" of the rectangle
* because the coordinate system is flipped.
* Note: if the input is inside the rectangle,
* the line segment wouldn't have an intersection with the rectangle,
* but the projected half-line does.
* Warning: passing in the middle of the rectangle will return the midpoint itself
* there are infinitely many half-lines projected in all directions,
* so let's just shortcut to midpoint (GIGO).
*
* @param x:Number x coordinate of point to build the half-line from
* @param y:Number y coordinate of point to build the half-line from
* @param minX:Number the "left" side of the rectangle
* @param minY:Number the "top" side of the rectangle
* @param maxX:Number the "right" side of the rectangle
* @param maxY:Number the "bottom" side of the rectangle
* @param validate:boolean (optional) whether to treat point inside the rect as error
* @return an object with x and y members for the intersection
* @throws if validate == true and (x,y) is inside the rectangle
* @author TWiStErRob
* @licence Dual CC0/WTFPL/Unlicence, whatever floats your boat
* @see <a href="http://stackru.com/a/31254199/253468">source</a>
* @see <a href="http://stackru.com/a/18292964/253468">based on</a>
*/
function pointOnRect(x, y, minX, minY, maxX, maxY, validate) {
//assert minX <= maxX;
//assert minY <= maxY;
if (validate && (minX < x && x < maxX) && (minY < y && y < maxY))
throw "Point " + [x,y] + "cannot be inside "
+ "the rectangle: " + [minX, minY] + " - " + [maxX, maxY] + ".";
var midX = (minX + maxX) / 2;
var midY = (minY + maxY) / 2;
// if (midX - x == 0) -> m == ±Inf -> minYx/maxYx == x (because value / ±Inf = ±0)
var m = (midY - y) / (midX - x);
if (x <= midX) { // check "left" side
var minXy = m * (minX - x) + y;
if (minY <= minXy && minXy <= maxY)
return {x: minX, y: minXy};
}
if (x >= midX) { // check "right" side
var maxXy = m * (maxX - x) + y;
if (minY <= maxXy && maxXy <= maxY)
return {x: maxX, y: maxXy};
}
if (y <= midY) { // check "top" side
var minYx = (minY - y) / m + x;
if (minX <= minYx && minYx <= maxX)
return {x: minYx, y: minY};
}
if (y >= midY) { // check "bottom" side
var maxYx = (maxY - y) / m + x;
if (minX <= maxYx && maxYx <= maxX)
return {x: maxYx, y: maxY};
}
// edge case when finding midpoint intersection: m = 0/0 = NaN
if (x === midX && y === midY) return {x: x, y: y};
// Should never happen :) If it does, please tell me!
throw "Cannot find intersection for " + [x,y]
+ " inside rectangle " + [minX, minY] + " - " + [maxX, maxY] + ".";
}
(function tests() {
var left = 100, right = 200, top = 50, bottom = 150; // a square, really
var hMiddle = (left + right) / 2, vMiddle = (top + bottom) / 2;
function intersectTestRect(x, y) { return pointOnRect(x,y, left,top, right,bottom, true); }
function intersectTestRectNoValidation(x, y) { return pointOnRect(x,y, left,top, right,bottom, false); }
function checkTestRect(x, y) { return function() { return pointOnRect(x,y, left,top, right,bottom, true); }; }
QUnit.test("intersects left side", function(assert) {
var leftOfRect = 0, closerLeftOfRect = 25;
assert.deepEqual(intersectTestRect(leftOfRect, 25), {x:left, y:75}, "point above top");
assert.deepEqual(intersectTestRect(closerLeftOfRect, top), {x:left, y:80}, "point in line with top");
assert.deepEqual(intersectTestRect(leftOfRect, 70), {x:left, y:90}, "point above middle");
assert.deepEqual(intersectTestRect(leftOfRect, vMiddle), {x:left, y:100}, "point exact middle");
assert.deepEqual(intersectTestRect(leftOfRect, 130), {x:left, y:110}, "point below middle");
assert.deepEqual(intersectTestRect(closerLeftOfRect, bottom), {x:left, y:120}, "point in line with bottom");
assert.deepEqual(intersectTestRect(leftOfRect, 175), {x:left, y:125}, "point below bottom");
});
QUnit.test("intersects right side", function(assert) {
var rightOfRect = 300, closerRightOfRect = 250;
assert.deepEqual(intersectTestRect(rightOfRect, 25), {x:right, y:75}, "point above top");
assert.deepEqual(intersectTestRect(closerRightOfRect, top), {x:right, y:75}, "point in line with top");
assert.deepEqual(intersectTestRect(rightOfRect, 70), {x:right, y:90}, "point above middle");
assert.deepEqual(intersectTestRect(rightOfRect, vMiddle), {x:right, y:100}, "point exact middle");
assert.deepEqual(intersectTestRect(rightOfRect, 130), {x:right, y:110}, "point below middle");
assert.deepEqual(intersectTestRect(closerRightOfRect, bottom), {x:right, y:125}, "point in line with bottom");
assert.deepEqual(intersectTestRect(rightOfRect, 175), {x:right, y:125}, "point below bottom");
});
QUnit.test("intersects top side", function(assert) {
var aboveRect = 0;
assert.deepEqual(intersectTestRect(80, aboveRect), {x:115, y:top}, "point left of left");
assert.deepEqual(intersectTestRect(left, aboveRect), {x:125, y:top}, "point in line with left");
assert.deepEqual(intersectTestRect(120, aboveRect), {x:135, y:top}, "point left of middle");
assert.deepEqual(intersectTestRect(hMiddle, aboveRect), {x:150, y:top}, "point exact middle");
assert.deepEqual(intersectTestRect(180, aboveRect), {x:165, y:top}, "point right of middle");
assert.deepEqual(intersectTestRect(right, aboveRect), {x:175, y:top}, "point in line with right");
assert.deepEqual(intersectTestRect(220, aboveRect), {x:185, y:top}, "point right of right");
});
QUnit.test("intersects bottom side", function(assert) {
var belowRect = 200;
assert.deepEqual(intersectTestRect(80, belowRect), {x:115, y:bottom}, "point left of left");
assert.deepEqual(intersectTestRect(left, belowRect), {x:125, y:bottom}, "point in line with left");
assert.deepEqual(intersectTestRect(120, belowRect), {x:135, y:bottom}, "point left of middle");
assert.deepEqual(intersectTestRect(hMiddle, belowRect), {x:150, y:bottom}, "point exact middle");
assert.deepEqual(intersectTestRect(180, belowRect), {x:165, y:bottom}, "point right of middle");
assert.deepEqual(intersectTestRect(right, belowRect), {x:175, y:bottom}, "point in line with right");
assert.deepEqual(intersectTestRect(220, belowRect), {x:185, y:bottom}, "point right of right");
});
QUnit.test("intersects a corner", function(assert) {
assert.deepEqual(intersectTestRect(left-50, top-50), {x:left, y:top}, "intersection line aligned with top-left corner");
assert.deepEqual(intersectTestRect(right+50, top-50), {x:right, y:top}, "intersection line aligned with top-right corner");
assert.deepEqual(intersectTestRect(left-50, bottom+50), {x:left, y:bottom}, "intersection line aligned with bottom-left corner");
assert.deepEqual(intersectTestRect(right+50, bottom+50), {x:right, y:bottom}, "intersection line aligned with bottom-right corner");
});
QUnit.test("on the corners", function(assert) {
assert.deepEqual(intersectTestRect(left, top), {x:left, y:top}, "top-left corner");
assert.deepEqual(intersectTestRect(right, top), {x:right, y:top}, "top-right corner");
assert.deepEqual(intersectTestRect(right, bottom), {x:right, y:bottom}, "bottom-right corner");
assert.deepEqual(intersectTestRect(left, bottom), {x:left, y:bottom}, "bottom-left corner");
});
QUnit.test("on the edges", function(assert) {
assert.deepEqual(intersectTestRect(hMiddle, top), {x:hMiddle, y:top}, "top edge");
assert.deepEqual(intersectTestRect(right, vMiddle), {x:right, y:vMiddle}, "right edge");
assert.deepEqual(intersectTestRect(hMiddle, bottom), {x:hMiddle, y:bottom}, "bottom edge");
assert.deepEqual(intersectTestRect(left, vMiddle), {x:left, y:vMiddle}, "left edge");
});
QUnit.test("validates inputs", function(assert) {
assert.throws(checkTestRect(hMiddle, vMiddle), /cannot be inside/, "center");
assert.throws(checkTestRect(hMiddle-10, vMiddle-10), /cannot be inside/, "top left of center");
assert.throws(checkTestRect(hMiddle-10, vMiddle), /cannot be inside/, "left of center");
assert.throws(checkTestRect(hMiddle-10, vMiddle+10), /cannot be inside/, "bottom left of center");
assert.throws(checkTestRect(hMiddle, vMiddle-10), /cannot be inside/, "above center");
assert.throws(checkTestRect(hMiddle, vMiddle), /cannot be inside/, "center");
assert.throws(checkTestRect(hMiddle, vMiddle+10), /cannot be inside/, "below center");
assert.throws(checkTestRect(hMiddle+10, vMiddle-10), /cannot be inside/, "top right of center");
assert.throws(checkTestRect(hMiddle+10, vMiddle), /cannot be inside/, "right of center");
assert.throws(checkTestRect(hMiddle+10, vMiddle+10), /cannot be inside/, "bottom right of center");
assert.throws(checkTestRect(left+10, vMiddle-10), /cannot be inside/, "right of left edge");
assert.throws(checkTestRect(left+10, vMiddle), /cannot be inside/, "right of left edge");
assert.throws(checkTestRect(left+10, vMiddle+10), /cannot be inside/, "right of left edge");
assert.throws(checkTestRect(right-10, vMiddle-10), /cannot be inside/, "left of right edge");
assert.throws(checkTestRect(right-10, vMiddle), /cannot be inside/, "left of right edge");
assert.throws(checkTestRect(right-10, vMiddle+10), /cannot be inside/, "left of right edge");
assert.throws(checkTestRect(hMiddle-10, top+10), /cannot be inside/, "below top edge");
assert.throws(checkTestRect(hMiddle, top+10), /cannot be inside/, "below top edge");
assert.throws(checkTestRect(hMiddle+10, top+10), /cannot be inside/, "below top edge");
assert.throws(checkTestRect(hMiddle-10, bottom-10), /cannot be inside/, "above bottom edge");
assert.throws(checkTestRect(hMiddle, bottom-10), /cannot be inside/, "above bottom edge");
assert.throws(checkTestRect(hMiddle+10, bottom-10), /cannot be inside/, "above bottom edge");
});
QUnit.test("doesn't validate inputs", function(assert) {
assert.deepEqual(intersectTestRectNoValidation(hMiddle-10, vMiddle-10), {x:left, y:top}, "top left of center");
assert.deepEqual(intersectTestRectNoValidation(hMiddle-10, vMiddle), {x:left, y:vMiddle}, "left of center");
assert.deepEqual(intersectTestRectNoValidation(hMiddle-10, vMiddle+10), {x:left, y:bottom}, "bottom left of center");
assert.deepEqual(intersectTestRectNoValidation(hMiddle, vMiddle-10), {x:hMiddle, y:top}, "above center");
assert.deepEqual(intersectTestRectNoValidation(hMiddle, vMiddle), {x:hMiddle, y:vMiddle}, "center");
assert.deepEqual(intersectTestRectNoValidation(hMiddle, vMiddle+10), {x:hMiddle, y:bottom}, "below center");
assert.deepEqual(intersectTestRectNoValidation(hMiddle+10, vMiddle-10), {x:right, y:top}, "top right of center");
assert.deepEqual(intersectTestRectNoValidation(hMiddle+10, vMiddle), {x:right, y:vMiddle}, "right of center");
assert.deepEqual(intersectTestRectNoValidation(hMiddle+10, vMiddle+10), {x:right, y:bottom}, "bottom right of center");
});
})();<link href="https://code.jquery.com/qunit/qunit-2.3.2.css" rel="stylesheet"/>
<script src="https://code.jquery.com/qunit/qunit-2.3.2.js"></script>
<div id="qunit"></div>Точка A всегда находится за пределами прямоугольника, а точка B всегда находится в центре прямоугольника.
Предполагая, что прямоугольник выровнен по оси, это упрощает задачу:
Наклон линии s = (Ay - By)/(Ax - Bx).
- Если -h/2 <= s * w/2 <= h/2, то линия пересекается:
- Правый край, если Ax > Bx
- Левый край, если Ax
- Если -w/2 <= (h/2)/s <= w/2, то линия пересекается:
- Верхний край, если Ay > By
- Нижний край, если Ay
Когда вы знаете, что край пересекается, вы узнаете одну координату: x = Bx ± w/2 или y = на ± h/2 в зависимости от того, по какому краю вы попали. Другая координата задается как y = By + s * w/2 или x = Bx + (h/2)/s.
Возможно, вы захотите проверить Graphics Gems - это классический набор процедур для графики и включает в себя множество необходимых алгоритмов. Несмотря на то, что он написан на C и немного устарел, алгоритмы по-прежнему блестят, и его легко перенести на другие языки.
Для вашей текущей задачи просто создайте четыре линии для прямоугольника и посмотрите, какие из них пересекают данную линию.
Вот решение в Java, которое возвращает истину, если линейный сегмент (первые 4 параметра) пересекает прямоугольник, выровненный по оси (последние 4 параметра). Было бы тривиально вернуть точку пересечения вместо логического. Это работает, сначала проверяя, если полностью вне, иначе используя уравнение линии y=m*x+b, Мы знаем, что линии, составляющие прямоугольник, выровнены по оси, поэтому проверки выполняются легко.
public boolean aabbContainsSegment (float x1, float y1, float x2, float y2, float minX, float minY, float maxX, float maxY) {
// Completely outside.
if ((x1 <= minX && x2 <= minX) || (y1 <= minY && y2 <= minY) || (x1 >= maxX && x2 >= maxX) || (y1 >= maxY && y2 >= maxY))
return false;
float m = (y2 - y1) / (x2 - x1);
float y = m * (minX - x1) + y1;
if (y > minY && y < maxY) return true;
y = m * (maxX - x1) + y1;
if (y > minY && y < maxY) return true;
float x = (minY - y1) / m + x1;
if (x > minX && x < maxX) return true;
x = (maxY - y1) / m + x1;
if (x > minX && x < maxX) return true;
return false;
}
Можно использовать ярлык, если начало или конец сегмента находится внутри прямоугольника, но, вероятно, лучше просто выполнить математику, которая всегда будет возвращать true, если один или оба конца сегмента находятся внутри. В любом случае, если вам нужен ярлык, вставьте код ниже после проверки "полностью снаружи".
// Start or end inside.
if ((x1 > minX && x1 < maxX && y1 > minY && y1 < maxY) || (x2 > minX && x2 < maxX && y2 > minY && y2 < maxY)) return true;
Учитывая первоначальный вопрос, я думаю, что ответ @ivanross на данный момент является наиболее кратким и ясным, и я обнаружил, что использую тот же подход.
Если у нас есть прямоугольник
- в центре В
- со сторонами, параллельными осям x и y
мы можем использовать немного тригонометрии, чтобы получить:
- тангенс φ (фи) = h/w
- тангенс θ (тета) = (yB-yA)/(xB-xA)
и некоторая тривиальная математика, чтобы получить, в каком квадранте (плоскости xy с центром в B) находится точка A.
наконец, мы сравниваем углы и используем касательные для вычисления координат точки пересечения, снова применяя основные принципы тригонометрии.
Вот решение, которое работает для меня. Я предполагаю, что прямоугольник выровнен по осям.
Данные:
// Center of the Rectangle
let Cx: number
let Cy: number
// Width
let w: number
// Height
let h: number
// Other Point
let Ax: number
let Ay: number
Теперь переведите точку A по центру прямоугольника, чтобы прямоугольник центрировался по O(0,0), и рассмотрите задачу в первой четверти (т.е. x > 0 и y > 0).
// Coordinates Translated
let Px = Math.abs(Ax - Cx)
let Py = Math.abs(Ay - Cy)
// Slope of line from Point P to Center
let Pm = Py / Px
// Slope of rectangle Diagonal
let Rm = h / w
// If the point is inside the rectangle, return the center
let res: [number, number] = [0, 0]
// Check if the point is inside and if so do not calculate
if (!(Px < w / 2 && Py < h / 2)) {
// Calculate point in first quarter: Px >= 0 && Py >= 0
if (Pm <= Rm) {
res[0] = w / 2
res[1] = (w * Pm) / 2
} else {
res[0] = h / (Pm * 2)
res[1] = h / 2
}
// Set original sign
if (Ax - Cx < 0) res[0] *= -1
if (Ay - Cy < 0) res[1] *= -1
}
// Translate back
return [res[0] + Cx, res[1] + Cy]
Сделаем некоторые предположения:
Точки
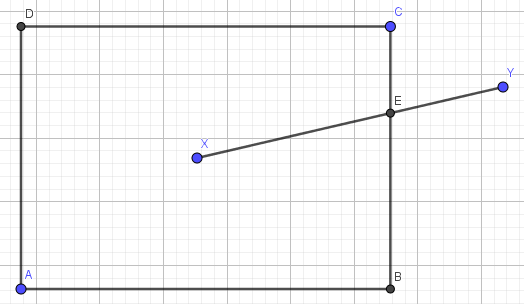
Aа такжеCданы, так что они определяют прямоугольникABCDсовмещен с традиционными топорами. Предположить, чтоAэто нижний левый угол, аCнаходится в правом верхнем углу (т.е.xA < xCа такжеyA < yC).Предположить, что
Xа такжеYданы две точки, такие чтоXлежит внутри прямоугольника (т.е.xA < xX < xC && yA < yX < yC) и Y лежит снаружи (т.е.not(xA < xY < xC && yA < yY < yC).
Это позволяет нам определить уникальную точку пересеченияE между сегментом [X,Y] и прямоугольник ∂ABCD.
Хитрость заключается в том, чтобы найти определенный 0 < t < 1 такой, что t*Y+(1-t)*X находится на прямоугольнике ∂ABCD. Переписав условиеΓ(t) ∈ ABCD в качестве:
(xY - xX) * t ∈ [xA - xX, xC - xX]а также(yY - yX) * t ∈ [yA - yX, yC - yX],
теперь есть возможность раскрутить все сценарии. Это дает:
var t = 0;
if(xY == xX) {
t = max((yA - yX)/(yY - yX), (yC - yX)/(yY - yX));
} else {
if(yY == yX) {
t = max((xA - xX)/(xY - xX), (xC - xX)/(xY - xX));
} else {
if(xY > xX) {
if(yY > yX) {
t = min((xC - xX)/(xY - xX), (yC - yX)/(yY - yX));
} else {
t = min((xC - xX)/(xY - xX), (yA - yX)/(yY - yX));
}
} else {
if(yY > yX) {
t = min((xA - xX)/(xY - xX), (yC - yX)/(yY - yX));
} else {
t = min((xA - xX)/(xY - xX), (yA - yX)/(yY - yX));
}
}
}
}
xE = t * xY + (1 - t) * xX;
yE = t * yY + (1 - t) * yX;
Я не фанат математики, и мне не особенно нравится переводить вещи с других языков, если другие уже сделали это, поэтому, когда я выполняю скучную задачу по переводу, я добавляю ее в статью, которая привела меня к коду. Чтобы никто не делал двойную работу.
Поэтому, если вы хотите иметь этот код пересечения в C#, посмотрите здесь http://dotnetbyexample.blogspot.nl/2013/09/utility-classes-to-check-if-lines-andor.html
Надеюсь, это сработает на 100%
У меня тоже была такая же проблема. Итак, после двух дней напряженных усилий я наконец создал этот метод,
Основной метод,
enum Line
{
// Inside the Rectangle so No Intersection Point(Both Entry Point and Exit Point will be Null)
InsideTheRectangle,
// One Point Inside the Rectangle another Line Outside the Rectangle. So it has only Entry Point
Entry,
// Both Point Outside the Rectangle but Intersecting. So It has both Entry and Exit Point
EntryExit,
// Both Point Outside the Rectangle and not Intersecting. So doesn't has both Entry and Exit Point
NoIntersection
}
// Tuple<entryPoint, exitPoint, lineStatus>
private Tuple<Point, Point, Line> GetIntersectionPoint(Point a, Point b, Rectangle rect)
{
if (IsWithinRectangle(a, rect) && IsWithinRectangle(b, rect))
{
// Can't set null to Point that's why I am returning just empty object
return new Tuple<Point, Point, Line>(new Point(), new Point(), Line.InsideTheRectangle);
}
else if (!IsWithinRectangle(a, rect) && !IsWithinRectangle(b, rect))
{
if (!LineIntersectsRectangle(a, b, rect))
{
// Can't set null to Point that's why I am returning just empty object
return new Tuple<Point, Point, Line>(new Point(), new Point(), Line.NoIntersection);
}
Point entryPoint = new Point();
Point exitPoint = new Point();
bool entryPointFound = false;
// Top Line of Chart Area
if (LineIntersectsLine(a, b, new Point(0, 0), new Point(rect.Width, 0)))
{
entryPoint = GetPointFromYValue(a, b, 0);
entryPointFound = true;
}
// Right Line of Chart Area
if (LineIntersectsLine(a, b, new Point(rect.Width, 0), new Point(rect.Width, rect.Height)))
{
if (entryPointFound)
exitPoint = GetPointFromXValue(a, b, rect.Width);
else
{
entryPoint = GetPointFromXValue(a, b, rect.Width);
entryPointFound = true;
}
}
// Bottom Line of Chart
if (LineIntersectsLine(a, b, new Point(0, rect.Height), new Point(rect.Width, rect.Height)))
{
if (entryPointFound)
exitPoint = GetPointFromYValue(a, b, rect.Height);
else
{
entryPoint = GetPointFromYValue(a, b, rect.Height);
}
}
// Left Line of Chart
if (LineIntersectsLine(a, b, new Point(0, 0), new Point(0, rect.Height)))
{
exitPoint = GetPointFromXValue(a, b, 0);
}
return new Tuple<Point, Point, Line>(entryPoint, exitPoint, Line.EntryExit);
}
else
{
Point entryPoint = GetEntryIntersectionPoint(rect, a, b);
return new Tuple<Point, Point, Line>(entryPoint, new Point(), Line.Entry);
}
}
Поддерживающие методы,
private Point GetEntryIntersectionPoint(Rectangle rect, Point a, Point b)
{
// For top line of the rectangle
if (LineIntersectsLine(new Point(0, 0), new Point(rect.Width, 0), a, b))
{
return GetPointFromYValue(a, b, 0);
}
// For right side line of the rectangle
else if (LineIntersectsLine(new Point(rect.Width, 0), new Point(rect.Width, rect.Height), a, b))
{
return GetPointFromXValue(a, b, rect.Width);
}
// For bottom line of the rectangle
else if (LineIntersectsLine(new Point(0, rect.Height), new Point(rect.Width, rect.Height), a, b))
{
return GetPointFromYValue(a, b, rect.Height);
}
// For left side line of the rectangle
else
{
return GetPointFromXValue(a, b, 0);
}
}
public bool LineIntersectsRectangle(Point p1, Point p2, Rectangle r)
{
return LineIntersectsLine(p1, p2, new Point(r.X, r.Y), new Point(r.X + r.Width, r.Y)) ||
LineIntersectsLine(p1, p2, new Point(r.X + r.Width, r.Y), new Point(r.X + r.Width, r.Y + r.Height)) ||
LineIntersectsLine(p1, p2, new Point(r.X + r.Width, r.Y + r.Height), new Point(r.X, r.Y + r.Height)) ||
LineIntersectsLine(p1, p2, new Point(r.X, r.Y + r.Height), new Point(r.X, r.Y)) ||
(r.Contains(p1) && r.Contains(p2));
}
private bool LineIntersectsLine(Point l1p1, Point l1p2, Point l2p1, Point l2p2)
{
float q = (l1p1.Y - l2p1.Y) * (l2p2.X - l2p1.X) - (l1p1.X - l2p1.X) * (l2p2.Y - l2p1.Y);
float d = (l1p2.X - l1p1.X) * (l2p2.Y - l2p1.Y) - (l1p2.Y - l1p1.Y) * (l2p2.X - l2p1.X);
if (d == 0)
{
return false;
}
float r = q / d;
q = (l1p1.Y - l2p1.Y) * (l1p2.X - l1p1.X) - (l1p1.X - l2p1.X) * (l1p2.Y - l1p1.Y);
float s = q / d;
if (r < 0 || r > 1 || s < 0 || s > 1)
{
return false;
}
return true;
}
// For Large values, processing with integer is not working properly
// So I here I am dealing only with double for high accuracy
private Point GetPointFromYValue(Point a, Point b, double y)
{
double x1 = a.X, x2 = b.X, y1 = a.Y, y2 = b.Y;
double x = (((y - y1) * (x2 - x1)) / (y2 - y1)) + x1;
return new Point((int)x, (int)y);
}
// For Large values, processing with integer is not working properly
// So here I am dealing only with double for high accuracy
private Point GetPointFromXValue(Point a, Point b, double x)
{
double x1 = a.X, x2 = b.X, y1 = a.Y, y2 = b.Y;
double y = (((x - x1) * (y2 - y1)) / (x2 - x1)) + y1;
return new Point((int)x, (int)y);
}
// rect.Contains(point) is not working properly in some cases.
// So here I created my own method
private bool IsWithinRectangle(Point a, Rectangle rect)
{
return a.X >= 0 && a.X <= rect.Width && a.Y >= 0 && a.Y <= rect.Height;
}
Я не дам вам программу для этого, но вот как вы можете это сделать:
- рассчитать угол наклона линии
- рассчитать угол линии от центра прямоугольника до одного из его углов
- на основе углов определить, с какой стороны линия пересекает прямоугольник
- рассчитать пересечение между стороной прямоугольника и линией
Другой вариант, который вы можете рассмотреть, особенно если вы планируете тестировать много линий с одним и тем же прямоугольником, - это преобразовать вашу систему координат, чтобы оси были выровнены по диагонали прямоугольника. Затем, так как ваша линия или луч начинаются в центре прямоугольника, вы можете определить угол, затем вы можете сказать, какой отрезок будет пересекаться по углу (т.е. <90 градусов сегмента 1, 90 градусов < <180 градусов сегмента 2 и т. Д.). Затем, конечно, вы должны преобразовать обратно в исходную систему координат
Хотя это кажется более трудоемким, матрицу преобразования и ее обратную можно вычислить один раз, а затем использовать повторно. Это также распространяется на прямоугольники с большими размерами, где вам придется учитывать квадранты и пересечения с гранями в 3D и так далее.
Вот немного многословный метод, который возвращает интервалы пересечения между (бесконечной) линией и прямоугольником, используя только основную математику:
// Line2 - 2D line with origin (= offset from 0,0) and direction
// Rectangle2 - 2D rectangle by min and max points
// Contacts - Stores entry and exit times of a line through a convex shape
Contacts findContacts(const Line2 &line, const Rectangle2 &rect) {
Contacts contacts;
// If the line is not parallel to the Y axis, find out when it will cross
// the limits of the rectangle horizontally
if(line.Direction.X != 0.0f) {
float leftTouch = (rect.Min.X - line.Origin.X) / line.Direction.X;
float rightTouch = (rect.Max.X - line.Origin.X) / line.Direction.X;
contacts.Entry = std::fmin(leftTouch, rightTouch);
contacts.Exit = std::fmax(leftTouch, rightTouch);
} else if((line.Offset.X < rect.Min.X) || (line.Offset.X >= rect.Max.X)) {
return Contacts::None; // Rectangle missed by vertical line
}
// If the line is not parallel to the X axis, find out when it will cross
// the limits of the rectangle vertically
if(line.Direction.Y != 0.0f) {
float topTouch = (rectangle.Min.Y - line.Offset.Y) / line.Direction.Y;
float bottomTouch = (rectangle.Max.Y - line.Offset.Y) / line.Direction.Y;
// If the line is parallel to the Y axis (and it goes through
// the rectangle), only the Y axis needs to be taken into account.
if(line.Direction.X == 0.0f) {
contacts.Entry = std::fmin(topTouch, bottomTouch);
contacts.Exit = std::fmax(topTouch, bottomTouch);
} else {
float verticalEntry = std::fmin(topTouch, bottomTouch);
float verticalExit = std::fmax(topTouch, bottomTouch);
// If the line already left the rectangle on one axis before entering it
// on the other, it has missed the rectangle.
if((verticalExit < contacts.Entry) || (contacts.Exit < verticalEntry)) {
return Contacts::None;
}
// Restrict the intervals from the X axis of the rectangle to where
// the line is also within the limits of the rectangle on the Y axis
contacts.Entry = std::fmax(verticalEntry, contacts.Entry);
contacts.Exit = std::fmin(verticalExit, contacts.Exit);
}
} else if((line.Offset.Y < rect.Min.Y) || (line.Offset.Y > rect.Max.Y)) {
return Contacts::None; // Rectangle missed by horizontal line
}
return contacts;
}
Этот подход обеспечивает высокую степень числовой устойчивости (интервалы во всех случаях являются результатом одного вычитания и деления), но включает некоторое ветвление.
Для отрезка линии (с начальной и конечной точками) вам нужно указать начальную точку сегмента в качестве начала и направления, end - start, Вычисление координат двух пересечений является простым как entryPoint = origin + direction * contacts.Entry а также exitPoint = origin + direction * contacts.Exit,
Я не знаю, является ли это лучшим способом, но что вы могли бы сделать, это выяснить пропорцию линии, которая находится внутри прямоугольника. Вы можете получить это из ширины прямоугольника и разницы между координатами x A и B (или высотой и координатами y; на основе ширины и высоты вы можете проверить, какой случай применяется, а другой случай будет на расширении стороны прямоугольника). Если у вас есть это, просто возьмите эту пропорцию вектора от B до A, и у вас есть координаты точки пересечения.
Приложив немного математики, вы можете решить эту проблему гораздо проще, чем предлагает большинство этих ответов.
Стратегия:
- Преобразуйте линию и прямоугольник так, чтобы центр прямоугольника находился в начале координат (0,0).
- Масштабируйте и линию, и прямоугольник по ширине/2 и высоте/2 прямоугольника (называемых xradius и yradius в моем примере кода ниже), поэтому проблема становится по существу «найти точку пересечения [линии между точкой p и началом координат] с [квадратом размера 2, центр которого находится в начале координат]».
- Теперь мы можем найти точку пересечения на ближайшей стороне квадрата, уменьшив координаты точки p так, чтобы она лежала на квадрате (сделав любую из координат равной +1 или -1).
- Поскольку проблема теперь симметрична, если мы возьмем абсолютные значения x и y, мы можем преобразовать (отразить) проблему только в «Квадрант 1» сетки, где x и y оба положительны. Это позволяет избежать индивидуальной обработки каждой стороны коробки.
- В квадранте 1 найдите точку пересечения. Если p выше линии x==y, нам нужно разделить на y, чтобы поместить точку на ближайшую линию, а если она ниже этой линии, нам нужно вместо этого разделить на x. Обратите внимание, что несмотря на то, что коэффициент масштабирования был рассчитан с использованием абсолютных значений координат x и y, его также можно использовать для масштабирования исходных координат.
- Теперь, когда у нас есть точка пересечения, выполните обратное преобразование, чтобы отменить преобразования из шага 2 и шага 1.
В С++ это выглядит примерно так:
struct point { double x, y; };
struct rect { point center; double xradius, yradius; }
point intersect(const point& p, const rect& r) {
// Steps 1 and 2: Transform to origin and scale by xradius and yradius.
point q{ (p.x - r.center.x) / r.xradius, (p.y - r.center.y) / r.yradius };
// Steps 3 and 4: Transform to Quadrant 1 and find scaling factor.
double f = max(abs(q.x), abs(q.y));
// Step 5: Divide by scaling factor to find intersection point on square.
point intersect{ q.x/f, q.y/f };
// Step 6: Inverse transformations from steps 1 and 2.
return {intersect.x * r.xradius + r.center.x, intersect.y * r.yradius + r.center.y};
}
если у вас есть доступ к истинному классу векторов и матриц с перегрузкой операторов, код становится еще проще:
point intersect(const point& p, const rect& r) {
matrix m = scale_matrix(r.xradius, r.yradius)*translate_matrix(p - r.center)
point q = m * p;
return m.inverse() * q/(max(abs(q.x), abs(q.y))
}
Предупреждение: этот код не обрабатывает случай, когда