Как понять обалденные шаги для дилетанта?
Сейчас я прохожу через numpy, и в numpy есть тема, которая называется "Шаги". Я понимаю, что это такое. Но как это работает? Я не нашел никакой полезной информации в Интернете. Кто-нибудь может дать мне понять с точки зрения непрофессионала?
2 ответа
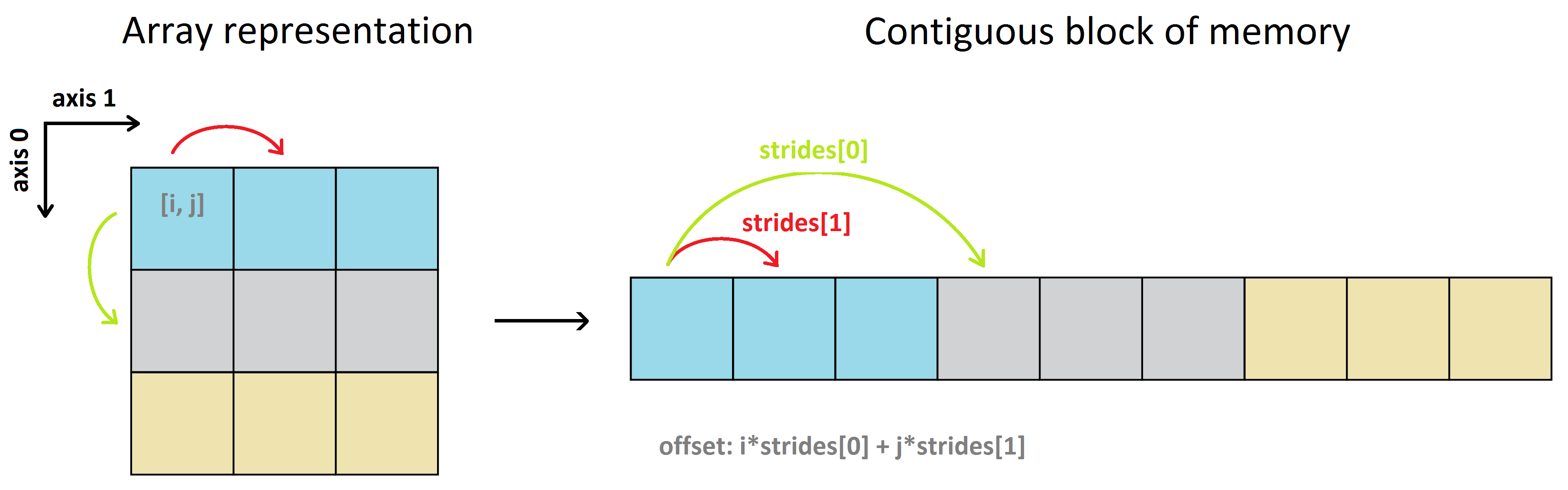
Фактические данные массива Numpy хранятся в однородном и непрерывном блоке памяти, называемом буфером данных. Для получения дополнительной информации см. Внутренности NumPy. Используя (по умолчанию) основной порядок строк, 2D-массив выглядит так:
Чтобы отобразить индексы i, j, k,... многомерного массива на позиции в буфере данных (смещение в байтах), NumPy использует понятие шагов. Шагов - это количество байтов, которые нужно перепрыгнуть в памяти, чтобы перейти от одного элемента к следующему элементу по каждому направлению / измерению массива. Другими словами, это разделение байтов между последовательными элементами для каждого измерения.
Например:
>>> a = np.arange(1,10).reshape(3,3)
>>> a
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
Этот двумерный массив имеет два направления: оси-0 (проходящие вертикально вниз по рядам) и ось-1 (проходящие горизонтально между столбцами), причем каждый элемент имеет размер:
>>> a.itemsize # in bytes
4
Итак, чтобы перейти от a[0, 0] -> a[0, 1] (перемещение по горизонтали вдоль 0-й строки, от 0-го столбца до 1-го столбца) шаг байта в буфере данных равен 4. То же самое для a[0, 1] -> a[0, 2], a[1, 0] -> a[1, 1] и т.д. Это означает, что количество шагов для горизонтального направления (ось-1) составляет 4 байта.
Тем не менее, чтобы перейти от a[0, 0] -> a[1, 0] (двигаясь по вертикали вдоль 0-го столбца, от 0-го ряда до 1-го ряда), вам нужно сначала пройти все оставшиеся элементы в 0-м ряду, чтобы добраться до 1-го ряда, а затем пройти через 1-й ряд, чтобы добраться до предмета. a[1, 0] т.е. a[0, 0] -> a[0, 1] -> a[0, 2] -> a[1, 0], Поэтому число шагов для вертикального направления (ось-0) составляет 3*4 = 12 байтов. Обратите внимание, что происходит от a[0, 2] -> a[1, 0] и, как правило, от последнего элемента i-й строки до первого элемента (i+1)-й строки также составляет 4 байта, поскольку массив a хранится в главном порядке строк.
Вот почему
>>> a.strides # (strides[0], strides[1])
(12, 4)
Вот еще один пример, показывающий, что шаги в горизонтальном направлении (ось-1), strides[1] двумерного массива необязательно равен размеру элемента (например, массив с основным порядком столбцов):
>>> b = np.array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]]).T
>>> b
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>> b.strides
(4, 12)
Вот strides[1] кратно размеру элемента. Хотя массив b выглядит идентично массиву a это другой массив: внутренне b хранится как |1|4|7|2|5|8|3|6|9| (потому что транспонирование не влияет на буфер данных, а только меняет шаги и форму), тогда как a как |1|2|3|4|5|6|7|8|9|, Что делает их похожими, так это разные шаги. То есть шаг байта для b[0, 0] -> b[0, 1] 3*4 = 12 байт и для b[0, 0] -> b[1, 0] 4 байта, тогда как для a[0, 0] -> a[0, 1] 4 байта и для a[0, 0] -> a[1, 0] 12 байт.
И последнее, но не менее важное: NumPy позволяет создавать виды существующих массивов с возможностью изменения шагов и формы, см. Трюки с шагами. Например:
>>> np.lib.stride_tricks.as_strided(a, shape=a.shape[::-1], strides=a.strides[::-1])
array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])
что эквивалентно транспонированию массива a,
Позвольте мне добавить, но не вдаваясь в подробности, что можно даже определить шаги, которые не кратны размеру предмета. Вот пример:
>>> a = np.lib.stride_tricks.as_strided(np.array([1, 512, 0, 3], dtype=np.int16),
shape=(3,), strides=(3,))
>>> a
array([1, 2, 3], dtype=int16)
>>> a.strides[0]
3
>>> a.itemsize
2
Просто чтобы добавить отличный ответ от @AndyK, я узнал об успехах Numpy MedKit. Там они показывают использование с проблемой следующим образом:
Учитывая вход:
x = np.arange(20).reshape([4, 5])
>>> x
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
Ожидаемый результат:
array([[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9]],
[[ 5, 6, 7, 8, 9],
[ 10, 11, 12, 13, 14]],
[[ 10, 11, 12, 13, 14],
[ 15, 16, 17, 18, 19]]])
Для этого нам нужно знать следующие термины:
shape - Размеры массива по каждой оси.
шаг - количество байтов памяти, которое необходимо пропустить, чтобы перейти к следующему элементу в определенном измерении.
>>> x.strides
(20, 4)
>>> np.int32().itemsize
4
Теперь, если мы посмотрим на ожидаемый результат:
array([[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9]],
[[ 5, 6, 7, 8, 9],
[ 10, 11, 12, 13, 14]],
[[ 10, 11, 12, 13, 14],
[ 15, 16, 17, 18, 19]]])
Нам нужно манипулировать формой массива и шагами. Выходная форма должна быть (3, 2, 5), то есть 3 элемента, каждый из которых содержит две строки (m == 2), а каждая строка имеет 5 элементов.
Шаг должен быть изменен с (20, 4) на (20, 20, 4). Каждый элемент в новом выходном массиве начинается с новой строки, каждая строка состоит из 20 байтов (5 элементов по 4 байта в каждом), а каждый элемент занимает 4 байта (int32).
Так:
>>> from numpy.lib import stride_tricks
>>> stride_tricks.as_strided(x, shape=(3, 2, 5),
strides=(20, 20, 4))
...
array([[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9]],
[[ 5, 6, 7, 8, 9],
[ 10, 11, 12, 13, 14]],
[[ 10, 11, 12, 13, 14],
[ 15, 16, 17, 18, 19]]])
Альтернативой будет:
>>> d = dict(x.__array_interface__)
>>> d['shape'] = (3, 2, 5)
>>> s['strides'] = (20, 20, 4)
>>> class Arr:
... __array_interface__ = d
... base = x
>>> np.array(Arr())
array([[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9]],
[[ 5, 6, 7, 8, 9],
[ 10, 11, 12, 13, 14]],
[[ 10, 11, 12, 13, 14],
[ 15, 16, 17, 18, 19]]])
Я использую этот метод очень часто вместо numpy.hstack или numpy.vstack и доверяю мне, в вычислительном отношении это намного быстрее.
Замечания:
При использовании очень больших массивов с этим трюком вычисление точных шагов не так тривиально. Я обычно делаю numpy.zeroes массив желаемой формы и получить шаги с помощью array.strides и использовать это в функции stride_tricks.as_strided,
Надеюсь, поможет!
Я адаптировал работу, представленную @Rick M., для решения моей проблемы, связанной с перемещением оконных нарезок numpy массивов любой формы. Вот код:
def sliding_window_slicing(a, no_items, item_type=0):
"""This method perfoms sliding window slicing of numpy arrays
Parameters
----------
a : numpy
An array to be slided in subarrays
no_items : int
Number of sliced arrays or elements in sliced arrays
item_type: int
Indicates if no_items is number of sliced arrays (item_type=0) or
number of elements in sliced array (item_type=1), by default 0
Return
------
numpy
Sliced numpy array
"""
if item_type == 0:
no_slices = no_items
no_elements = len(a) + 1 - no_slices
if no_elements <=0:
raise ValueError('Sliding slicing not possible, no_items is larger than ' + str(len(a)))
else:
no_elements = no_items
no_slices = len(a) - no_elements + 1
if no_slices <=0:
raise ValueError('Sliding slicing not possible, no_items is larger than ' + str(len(a)))
subarray_shape = a.shape[1:]
shape_cfg = (no_slices, no_elements) + subarray_shape
strides_cfg = (a.strides[0],) + a.strides
as_strided = np.lib.stride_tricks.as_strided #shorthand
return as_strided(a, shape=shape_cfg, strides=strides_cfg)
Этот метод автоматически рассчитает шаги, и она работает с Numpy массивами любых размеров:
1D массив - нарезка по ряду срезов
In [11]: a
Out[11]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [12]: sliding_window_slicing(a, 5, item_type=0)
Out[12]:
array([[0, 1, 2, 3, 4, 5],
[1, 2, 3, 4, 5, 6],
[2, 3, 4, 5, 6, 7],
[3, 4, 5, 6, 7, 8],
[4, 5, 6, 7, 8, 9]])
1D-массив - нарезка по количеству элементов на срез
In [13]: sliding_window_slicing(a, 5, item_type=1)
Out[13]:
array([[0, 1, 2, 3, 4],
[1, 2, 3, 4, 5],
[2, 3, 4, 5, 6],
[3, 4, 5, 6, 7],
[4, 5, 6, 7, 8],
[5, 6, 7, 8, 9]])
2D-массив - нарезка по ряду срезов
In [16]: a = np.arange(10).reshape([5,2])
In [17]: a
Out[17]:
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
In [18]: sliding_window_slicing(a, 2, item_type=0)
Out[18]:
array([[[0, 1],
[2, 3],
[4, 5],
[6, 7]],
[[2, 3],
[4, 5],
[6, 7],
[8, 9]]])
2D-массив - нарезка по количеству элементов на срез
In [19]: sliding_window_slicing(a, 2, item_type=1)
Out[19]:
array([[[0, 1],
[2, 3]],
[[2, 3],
[4, 5]],
[[4, 5],
[6, 7]],
[[6, 7],
[8, 9]]])