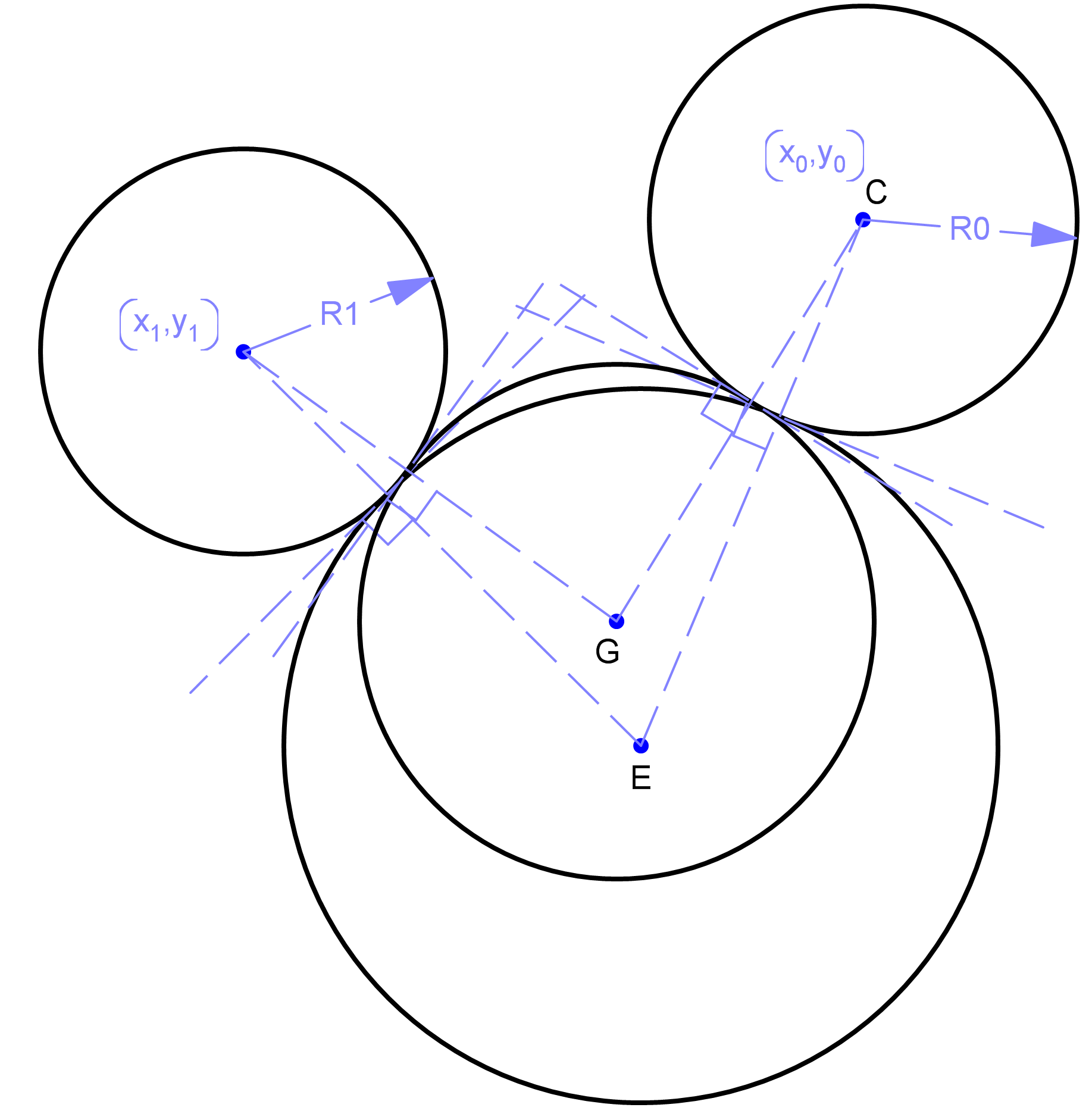
Вычисление касательной дуги между двумя точками на двух окружностях
Как я могу рассчитать дугу между двумя кругами? Дуга должна касаться двух точек на окружностях.
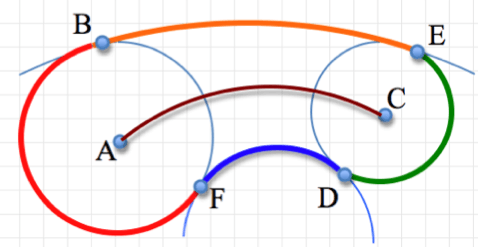
Вот картинка, иллюстрирующая это. Я пытаюсь закодировать и вычислить оранжевую и синюю дуги.
больше деталей:
Ваш апплет должен иметь 2 режима: 2D и 3D. Пользователь должен иметь возможность переключаться между ними, нажимая клавишу пробела. В режиме 2D пользователь может редактировать положение четырех контрольных точек A, B, C и D и должен видеть 4 дуги окружности, определяемые этими точками следующим образом. Красная дуга лежит на окружности центра A и радиуса ||AB||. Зеленая дуга лежит на окружности центра C и радиуса ||CD||. Оранжевая дуга лежит на опорном окружности, касательной к опорной окружности красной дуги в точке В, а также по касательной к окружности в зеленой точке Е, который ваш код должен вычислить. Этот поддерживающий круг не должен отделять A и C (т. Е. A и C должны быть либо в этом круге, либо вне его). Кроме того, синий дуга лежит на окружности, которая не разделяет А и С, а по касательной к опорной окружности зеленой дуги на D, а также по касательной к опорной окружности красной дуги в некоторой точке Р, ваша программа должна вычислить. Красная дуга проходит по часовой стрелке от F до B. Оранжевая дуга проходит от B до E. Зеленая дуга проходит от E до D. Синяя дуга идет от D обратно к F. Эти четыре дуги образуют плавную границу области S из самолет. Обратите внимание, что в зависимости от положения контрольных точек оранжевая и синяя дуги могут быть либо вогнутыми, либо выпуклыми. На рисунке ниже синяя дуга вогнутая. (на фото выше)
3 ответа
Вообще говоря, вы не можете. Проведите прямые линии через AB и CE и вытяните их до точки пересечения. Назовите пересечение M. Вы можете провести дугу через B и E, которая касается окружностей тогда и только тогда, когда BM = EM.
Пусть G - центр круга для дуги между B и E, а H - круг для дуги между F и D.
Ключевым моментом является то, что линия, которая пересекает окружность, является касательной, если и только если она перпендикулярна радиусу в точке пересечения. Это означает, что если у вас есть две окружности, которые касаются, то точка касания и центры окружностей коллинеарны.
Таким образом, это означает, что центр G является пересечением линии, определенной B и A, и линией, определенной E и C. Аналогично, центр H является пересечением линии, определенной A и F, и линии, определенной C и D.
Учитывая эти центры, вы можете определить радиусы двух окружностей просто от расстояния от центра до точки касания. Оттуда вы можете использовать стандартные методы для рисования дуги с учетом ее конечных точек и круга, частью которого она является.