Очень быстрый метод для аппроксимации np.random.dirichlet с большой размерностью

Question

Я хотел бы оценить np.random.dirichlet с большим размером как можно быстрее. Точнее, я хотел бы функцию, аппроксимирующую ниже, по крайней мере, в 10 раз быстрее. Опытным путем я заметил, что версия этой функции для малого размера выводит одну или две записи, которые имеют порядок 0,1, а все остальные записи настолько малы, что они несущественны. Но это наблюдение не основано на какой-либо строгой оценке. Приближение не должно быть таким точным, но я хочу что-то не слишком грубое, так как я использую этот шум для MCTS.

def g():
   np.random.dirichlet([0.03]*4840)

>>> timeit.timeit(g,number=1000)
0.35117408499991143

Answer 1

Предполагая, что ваша альфа фиксирована по компонентам и используется для многих итераций, вы можете составить таблицу ppf соответствующего гамма-распределения. Это, вероятно, доступно как scipy.stats.gamma.ppf но мы также можем использовать scipy.special.gammaincinv, Эта функция кажется довольно медленной, так что это существенные предварительные инвестиции.

Вот грубая реализация общей идеи:

import numpy as np
from scipy import special

class symm_dirichlet:
    def __init__(self, alpha, resolution=2**16):
        self.alpha = alpha
        self.resolution = resolution
        self.range, delta = np.linspace(0, 1, resolution,
                                        endpoint=False, retstep=True)
        self.range += delta / 2
        self.table = special.gammaincinv(self.alpha, self.range)
    def draw(self, n_sampl, n_comp, interp='nearest'):
        if interp != 'nearest':
            raise NotImplementedError
        gamma = self.table[np.random.randint(0, self.resolution,
                                             (n_sampl, n_comp))]
        return gamma / gamma.sum(axis=1, keepdims=True)

import time, timeit

t0 = time.perf_counter()
X = symm_dirichlet(0.03)
t1 = time.perf_counter()
print(f'Upfront cost {t1-t0:.3f} sec')
print('Running cost per 1000 samples of width 4840')
print('tabulated           {:3f} sec'.format(timeit.timeit(
    'X.draw(1, 4840)', number=1000, globals=globals())))
print('np.random.dirichlet {:3f} sec'.format(timeit.timeit(
    'np.random.dirichlet([0.03]*4840)', number=1000, globals=globals())))

Образец вывода:

Upfront cost 13.067 sec
Running cost per 1000 samples of width 4840
tabulated           0.059365 sec
np.random.dirichlet 0.980067 sec

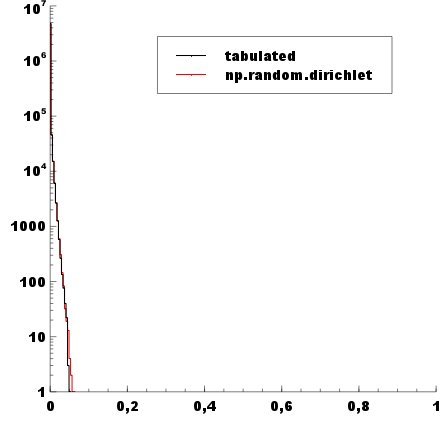
Лучше проверить, правильно ли это: