R-уравнение (уравнение Никольского-Эйзенмана) к данным
Раньше я использовал SigmaPlot, чтобы соответствовать модифицированной версии уравнения Никольского-Эйзенмана в форме
y = P1 + P2 * log(10^(-x) + P3)
используя функцию подбора глобальной кривой. Детали параметров можно найти в отчете Sigmaplot ниже. Я хочу сделать это сейчас в R.
Некоторые данные:
pNO3 <- c(1.1203, 2.0410, 3.0155, 4.0048, 4.3045, 5.0, 6.0)
mV <- c(45.2, 100.9, 160.9, 215.7, 231.5, 244.5, 257.4)
data <- data.frame(pNO3, mV)
plot(data$pNO3, data$mV)
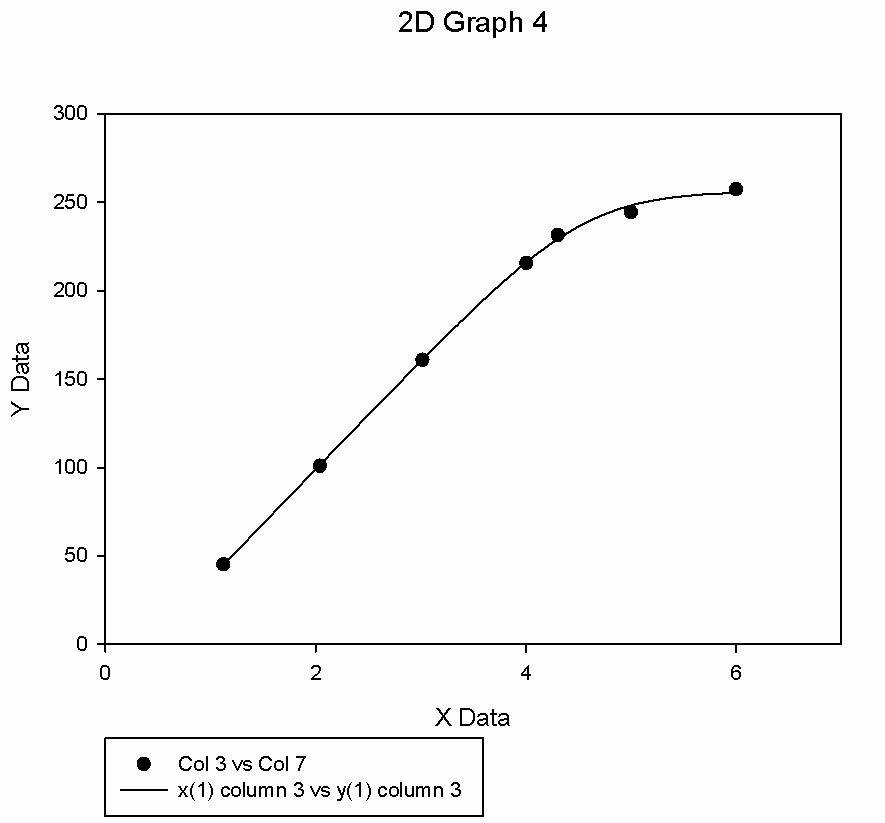
График и отчет, сгенерированный sigmaplot для вышеуказанных данных, показан ниже. Может кто-нибудь указать мне в правильном направлении, как создать нечто подобное в R?
NonLinear Regression - Global Curve Fitting Wednesday, May 01, 2013, 13:04:55
Data Source: Data 1 in Notebook1
Equation: User-Defined, Nicolsky Eisenman
f=P1+P2*log(10^(-x)+P3)
Data Set Specifications:
Data Set Independent Variable Dependent Variable
1 Column 3 Column 7
Global Parameters:
A Global Parameter is shared across all data sets.
Global Goodness of Fit:
R Rsqr Adj Rsqr Standard Error of Estimate
0.9997 0.9994 0.9991 2.4421
Analysis of Variance:
Analysis of Variance:
DF SS MS
Regression 3 264242.5551 88080.8517
Residual 4 23.8549 5.9637
Total 7 264266.4100 37752.3443
Corrected for the mean of the observations:
DF SS MS F P
Regression 2 38844.3822 19422.1911 3256.7192 <0.0001
Residual 4 23.8549 5.9637
Total 6 38868.2371 6478.0395
Statistical Tests:
Normality Test (Shapiro-Wilk) Passed (P = 0.4003)
W Statistic= 0.9106 Significance Level = 0.0500
Constant Variance Test Passed (P = 0.1209)
Number of Observations = 7
Rsqr = 0.9994
Residual Sum of Squares = 23.8549
Parameter Estimates:
Coefficient Std. Error t P
P1 -24.3265 3.3330 -7.2987 0.0019
P2 -61.7088 1.2861 -47.9796 <0.0001
P3 2.8351E-005 4.6040E-006 6.1579 0.0035
Fit Equation Description:
[Variables]
f0_x = col(3)
f0_y = col(7)
[Parameters]
f0_P1 = 0 ' {{previous: -24.3265}}
f0_P2 = -5 ' {{previous: -61.7088}}
f0_P3 = 0 ' {{previous: 2.8351e-005}}
[Equation]
f0 = f0_P1+f0_P2*log(10^(-f0_x)+f0_P3)
fit f0 to f0_y
[Constraints]
[Options]
tolerance=0.000100
stepsize=100
iterations=100
Number of Iterations Performed = 4
2 ответа
Предполагая, что ваш критерий подгонки сводит к минимуму сумму квадратов ошибок, вы можете использовать nls, но вам нужна справедливая стартовая стоимость. Я понятия не имею, что является разумным для ваших параметров, поэтому я потратил некоторое время, пока скопировал параметры из вашего примера sigmaplot, что, я думаю, было разумно для этого набора данных, который может быть похож на этот набор данных. В любом случае, если вы знаете, что означают параметры, вы, вероятно, сможете угадать разумные начальные значения.
> start=list(P1=-24,P2=-61,P3=2.8e-5)
> m = nls(formula= mV ~ P1 + P2 * log(10^(-pNO3) + P3),data=data,start=start)
> summary(m)
Formula: mV ~ P1 + P2 * log(10^(-pNO3) + P3)
Parameters:
Estimate Std. Error t value Pr(>|t|)
P1 -1.420e+01 4.642e+00 -3.059 0.055 .
P2 -2.732e+01 9.257e-01 -29.514 8.54e-05 ***
P3 8.417e-05 1.818e-05 4.630 0.019 *
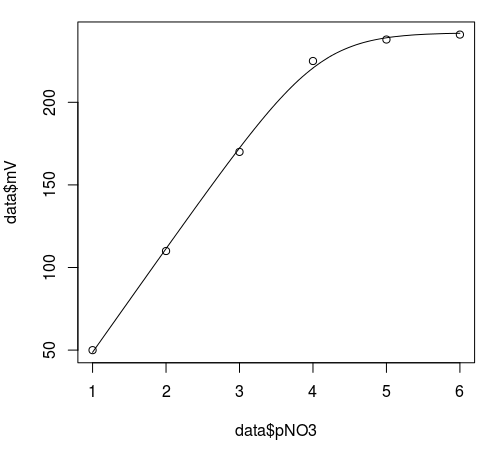
Вы можете нанести данные и подгонку плавной кривой, создав новый набор pNO3 меры:
plot(data$pNO3,data$mV)
newdata = data.frame(pNO3=seq(1,6,len=100))
lines(newdata$pNO3,predict(m, newdata=newdata))
Обратите внимание, что "log" - это натуральный логарифм в R, если вы хотите записать в основание 10, используйте log10 - это немного меняет P2, примерно до -62 вместо -27, как указано выше...
С вашими новыми данными и с "log10" вместо "log" в выражении формулы я получаю:
> m10 = nls(formula= mV ~ P1 + P2 * log10(10^(-pNO3) + P3),data=data,start=start)
> summary(m10)
Formula: mV ~ P1 + P2 * log10(10^(-pNO3) + P3)
Parameters:
Estimate Std. Error t value Pr(>|t|)
P1 -2.433e+01 3.334e+00 -7.298 0.00187 **
P2 -6.171e+01 1.286e+00 -47.972 1.13e-06 ***
P3 2.835e-05 4.605e-06 6.157 0.00353 **
Как выглядит ваш вывод Sigmaplot:
Parameter Estimates:
Coefficient Std. Error t P
P1 -24.3265 3.3330 -7.2987 0.0019
P2 -61.7088 1.2861 -47.9796 <0.0001
P3 2.8351E-005 4.6040E-006 6.1579 0.0035
С "plinear" алгоритм nls только параметры, которые вводятся нелинейно, требуют начальных значений. Обратите внимание, что plinear требует изменения формулы, как показано для представления этой модели:
fo <- mV ~ cbind(log10(10^(-pNO3) + P3), 1)
fm <- nls(fo, data, start = c(P3 = 0), alg = "plinear")
summary(fm)
давая:
Formula: mV ~ cbind(log10(10^(-pNO3) + P3), 1)
Parameters:
Estimate Std. Error t value Pr(>|t|)
P3 2.84e-05 4.60e-06 6.16 0.0035 **
.lin1 -6.17e+01 1.29e+00 -47.97 1.1e-06 ***
.lin2 -2.43e+01 3.33e+00 -7.30 0.0019 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.44 on 4 degrees of freedom
Number of iterations to convergence: 7
Achieved convergence tolerance: 2.94e-06
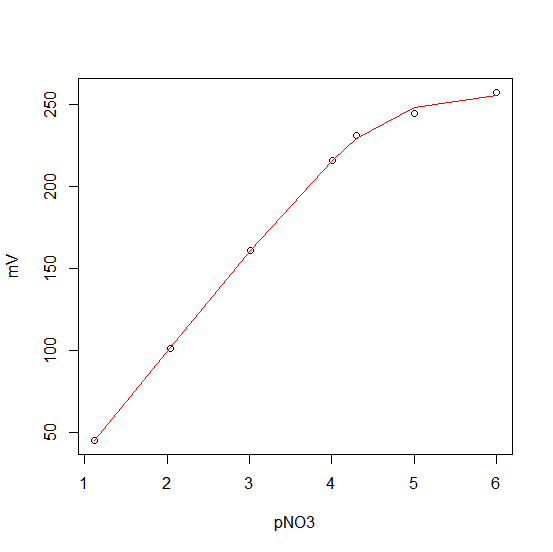
И мы можем построить это так:
plot(data)
lines(fitted(fm) ~ pNO3, data, col = "red")