Cepstral Анализ для обнаружения основного тона

Question

Я ищу, чтобы извлечь смолы из звукового сигнала.

Кто-то из IRC только что объяснил мне, как это достигается благодаря двойному БПФ. В частности:

1. взять БПФ
2. взять журнал квадрата абсолютного значения (можно сделать с помощью таблицы поиска)
3. взять еще один БПФ
4. принять абсолютное значение

Я пытаюсь это с помощью vDSP

Я не могу понять, как я не сталкивался с этой техникой раньше. Я много охотился и задавал вопросы; стоит несколько недель. Более того, я не могу понять, почему я не подумал об этом.

Я пытаюсь достичь этого с помощью библиотеки vDSP. Похоже, что он имеет функции для решения всех этих задач.

Однако меня интересует точность итогового результата.

Ранее я использовал технику, которая ищет частотные интервалы одного БПФ для локальных максимумов. Когда он сталкивается с одним из них, он использует хитрый метод (изменение фазы со времени последнего БПФ), чтобы более точно разместить фактический пик в ячейке.

Я беспокоюсь, что эта точность будет потеряна с помощью этой техники, которую я здесь представляю.

Я полагаю, что эту технику можно использовать после второго БПФ, чтобы точно получить фундаментальное значение. Но похоже, что информация теряется на шаге 2.

Поскольку это потенциально сложный процесс, может ли кто-то с некоторым опытом просто посмотреть, что я делаю, и проверить это на здравомыслие?

Кроме того, я слышал, что есть альтернативный метод, включающий подгонку квадратика к соседним лоткам. Это сопоставимая точность? Если это так, я бы предпочел это, так как это не связано с запоминанием фаз бина.

Итак, вопросы:

• имеет ли этот подход смысл? Можно ли это улучшить?
• Я немного беспокоюсь о компоненте "log square"; похоже, что для этого есть функция vDSP: vDSP_vdbcon. Тем не менее, нет никаких признаков того, что он предварительно вычисляет таблицу журнала - я предполагаю, что это не так, поскольку функция FFT требует, чтобы явная функция предварительного вычисления была вызвана и передана в нее. И эта функция не делает.
• Есть ли какая-то опасность попадания гармоник?
• Есть ли какой-нибудь хитрый способ заставить vDSP извлекать максимумы, сначала самые большие?

• Кто-нибудь может указать мне на некоторые исследования или литературу по этой технике?

• главный вопрос: достаточно ли это точно? Можно ли улучшить точность? Мне только что сказал эксперт, что точность INDEED недостаточна. Это конец линии?

число Пи

PS Я очень раздражен, когда хочу создать теги, но не могу.:| Я предложил сопровождающим, чтобы ТАК отслеживал предпринятые теги, но я уверен, что меня проигнорировали. Нам нужны теги для vDSP, ускорение фреймворка, кепстральный анализ

Answer 1

Хорошо, давайте пройдемся по одному:

Я ищу, чтобы извлечь смолы из звукового сигнала.

Хотя я не эксперт и прошел минимальную формальную подготовку, я думаю, что знаю лучший ответ на эту проблему. За последние несколько лет я много занимался поиском, чтением и экспериментами. Я согласен с тем, что метод автокорреляции является безусловно лучшим детектором основного тона с точки зрения компромисса между точностью, сложностью, помехоустойчивостью и скоростью. Если у вас нет особых обстоятельств, я бы почти всегда рекомендовал использовать автокорреляцию. Подробнее об этом позже, позвольте мне ответить на ваши другие вопросы.

То, что вы описываете, это "кепстральный анализ", который используется в основном для извлечения высоты тона из речи. Цепстральный анализ полностью зависит от обилия и силы обертонов вашего сигнала. Например, если вы проведете чистую синусоидальную волну через кепстральный анализ, вы получите ужасные результаты. Однако для речи, которая является сложным сигналом, существует большое количество обертонов. (Между прочим, обертоны - это элементы сигнала, которые колеблются с кратностью основной частоты, то есть высоты, которую мы воспринимаем). Цепстральный анализ может быть надежным при обнаружении речи с отсутствующей основной частотой. То есть предположим, что вы построили функцию sin (4x) + sin (6x) + sin (8x) + sin (10x). Если вы посмотрите на это, то ясно, что оно имеет ту же частоту, что и функция sin(2x). Однако, если вы примените к этой функции анализ Фурье, ячейка, соответствующая sin (2x), будет иметь нулевую величину. Таким образом, считается, что этот сигнал имеет "отсутствующую основную частоту", потому что он не содержит синусоиды частоты, которой мы считаем ее. Таким образом, простое выделение самого большого пика преобразования Фурье не будет работать с этим сигналом.

Ранее я использовал технику, которая ищет частотные интервалы одного БПФ для локальных максимумов. когда он сталкивается с одним из них, он использует хитрый метод (изменение фазы со времени последнего БПФ), чтобы более точно разместить фактический пик в ячейке.

То, что вы описываете, это метод фазового вокодера для более точного измерения частоты данного партиала. Тем не менее, основной метод выбора самого большого приемника вызовет у вас проблемы, если вы используете сигнал с отсутствующим или слабым компонентом основной частоты.

Я беспокоюсь, что эта точность будет потеряна с помощью этой техники, которую я здесь представляю.

Прежде всего, помните, что метод фазового вокодера только более точно измеряет частоту одного частичного. Он игнорирует информацию, содержащуюся в более высоких частях об основной частоте. Во-вторых, учитывая приличный размер БПФ, вы можете получить очень хорошую точность, используя пиковую интерполяцию. Кто-то еще указал вам на параболическую интерполяцию. Я также хотел бы предложить это.

Если вы параболически интерполируете FFT блока данных 4098 с частотой 44100 Гц с шагом около 440 Гц, это будет означать, что он будет между 40-м (430,66 Гц) и 41-м (441,430664064) бином. Предполагая, что эта статья приблизительно верна в общем случае, она говорит, что параболическая интерполяция увеличивает разрешение более чем на один порядок. Это оставляет разрешение не менее 1 Гц, что является порогом человеческого слуха. На самом деле, если вы используете идеальное гауссовское окно, параболическая интерполяция является точной на пиках (это верно, точно. Помните, однако, что вы никогда не сможете использовать настоящее гауссовское окно, потому что оно расширяется навсегда в обоих направлениях.) Если вы все еще волнуясь о получении более высокой точности, вы всегда можете дополнить БПФ. Это означает добавление нулей в конец БПФ перед преобразованием. Выясняется, что это эквивалентно "синхрополярной интерполяции", которая является идеальной функцией интерполяции для сигналов с ограниченной частотой.

Я полагаю, что эту технику можно использовать после второго БПФ, чтобы точно получить фундаментальное значение. Но похоже, что информация теряется на шаге 2.

Это правильно. Метод фазового вокодера основан на том факте, что последовательные кадры связаны и имеют определенное фазовое соотношение. Тем не менее, логарифмическая величина БПФ последовательных кадров не показывает такую ​​же взаимосвязь с точки зрения фазы, поэтому было бы бесполезно использовать это преобразование для второго БПФ.

• имеет ли этот подход смысл? Можно ли это улучшить?

Да и да, в конце я подробно остановлюсь на улучшении автокорреляции.

• Я немного обеспокоен И компонентом квадратного сечения; Кажется, есть функция vDSP, которая делает именно это: vDSP_vdbcon, однако, нет никаких указаний на то, что она предварительно вычисляет таблицу журналов - я предполагаю, что это не так, поскольку функция FFT требует, чтобы явная функция предварительного вычисления была вызвана и передана внутрь. и эта функция не делает.

Я не знаю специфики библиотеки vDSP, извините.

• Есть ли какая-то опасность попадания гармоник?

В вашей оригинальной фазо-вокодерной технике выбора пиков? да. С кепстральным методом? нет, не совсем, весь смысл в том, что он рассматривает все гармоники, чтобы получить свою оценку частоты. Например, скажем, наша частота равна 1. Наши обертоны 2,3,4,5,6,7,8,9, и т. Д. Мы должны были бы убрать все нечетные гармоники, т.е. оставить 2,4,6,8 и т. Д., И удалите основную частоту, прежде чем ее начнут путать с одним из ее обертонов.

• Есть ли какой-нибудь хитрый способ заставить vDSP извлекать максимумы, сначала самые большие?

Не знаю vDSP, но в общем случае вы обычно просто перебираете все из них и отслеживаете самое большое.

• Кто-нибудь может указать мне на некоторые исследования или литературу по этой технике?

Ссылка, которую я дал вам в комментарии, казалась хорошей.

Кроме того, этот сайт предлагает невероятно глубокое и удивительно широкое объяснение тем DSP, включая все виды извлечения высоты тона, манипуляции и т. Д., Как теоретическим, так и практическим способом. ( это более общая ссылка на индекс на сайте). Я всегда возвращаюсь к этому. Иногда это может быть немного ошеломляющим, если вы прыгаете в середину, но вы всегда можете следовать каждому объяснению обратно к основным строительным блокам.

Теперь для автокорреляции. В основном техника такова: вы берете ваш (оконный) сигнал и время задержки его в разном количестве. Найдите сумму, которая лучше всего соответствует вашему исходному сигналу. Это фундаментальный период. Это имеет большой теоретический смысл. Вы охотитесь за повторяющимися частями вашего сигнала.

На практике получение корреляции со всеми этими задержанными по времени копиями сигнала происходит медленно. Вместо этого он обычно реализуется следующим образом (что математически эквивалентно):

Zero-Pad это удвоить его первоначальную длину. Возьмите БПФ. Затем замените все коэффициенты их квадратной величиной, кроме первого, для которого вы установили 0. Теперь возьмите IFFT. Разделите каждый элемент на первый. Это дает вам автокорреляцию. Математически вы используете теорему о круговой свертке (ищите ее) и используете заполнение нулями для преобразования задачи линейной свертки в задачу с круговой сверткой, которая может быть эффективно решена.

Однако будьте осторожны при выборе вершины. При очень малых задержках сигнал очень хорошо согласуется с самим собой, просто потому, что он непрерывный. (Я имею в виду, если вы откладываете его на ноль, он идеально соотносится с самим собой). Вместо этого выберите самый большой пик после первого пересечения нуля. Вы можете параболически интерполировать функцию автокорреляции так же, как и другие методы, чтобы получить гораздо более точные значения.

Это само по себе даст вам очень хорошее обнаружение высоты тона по всем критериям. Тем не менее, иногда вы можете столкнуться с проблемой уменьшения вдвое и удвоения высоты. В основном проблема заключается в том, что если сигнал повторяется каждые 1 секунду, он также повторяется каждые две секунды. Точно так же, если у него очень сильный обертон, вы можете получить половину высоты тона. Так что самая большая вершина не всегда может быть той, которую вы хотите. Решением этой проблемы является алгоритм MPM Филиппа МакЛауда. Идея заключается в следующем:

Вместо того, чтобы выбирать самую большую вершину, вы хотите выбрать первую вершину, которая достаточно велика для рассмотрения. Как вы определяете, является ли пик достаточно большим, чтобы его можно было рассмотреть? Если он, по крайней мере, так же высок, как A*, самый большой пик, где A - некоторая постоянная величина. Я думаю, что Филипп предлагает значение А около 0,9. На самом деле программа, которую он написал, Tartini, позволяет сравнивать несколько разных алгоритмов определения высоты звука в реальном времени. Я настоятельно рекомендую загрузить его и опробовать (в нем реализован Cepstrum, прямая автокорреляция и MPM): (если у вас проблемы со сборкой, попробуйте инструкции здесь.

И последнее, что я должен отметить, - это создание окон. В общем, подойдет любое гладкое окно. Окно Ханнинга, окно Хэмминга и т. Д. Надеюсь, вы должны знать, как окно. Я бы также предложил сделать перекрывающиеся окна, если вы хотите более точные временные измерения.

Кстати, классная особенность автокорреляции заключается в том, что если частота измеряется линейно по оконному участку, который вы измеряете, это даст вам правильную частоту в центре окна.

Еще одна вещь: то, что я описал, называется смещенной функцией автокорреляции. Это связано с тем, что для более высоких временных задержек перекрытие между исходным сигналом и версией с временной задержкой становится все меньше и меньше. Например, если вы посмотрите на окно размера N, в котором было задержано N-1 выборок, вы увидите, что перекрывается только одна выборка. Таким образом, корреляция при этой задержке, очевидно, будет очень близка к нулю. Вы можете компенсировать это, погружая каждое значение функции автокорреляции на количество перекрывающихся выборок, чтобы получить его. Это называется беспристрастной автокорреляцией. Однако, в целом, вы получите худшие результаты с этим, поскольку более высокие значения задержки автокорреляции очень шумные, так как они основаны только на нескольких выборках, поэтому имеет смысл взвешивать их меньше.

Если вы ищете дополнительную информацию, как всегда, Google - ваш друг. Хорошие условия поиска: автокорреляция, определение высоты тона, отслеживание высоты тона, извлечение высоты тона, оценка высоты тона, кепстр и т. Д.

Answer 2

Это краткий анализ кепстра, используемого для определения высоты тона.

Сначала давайте рассмотрим синтетический сигнал.

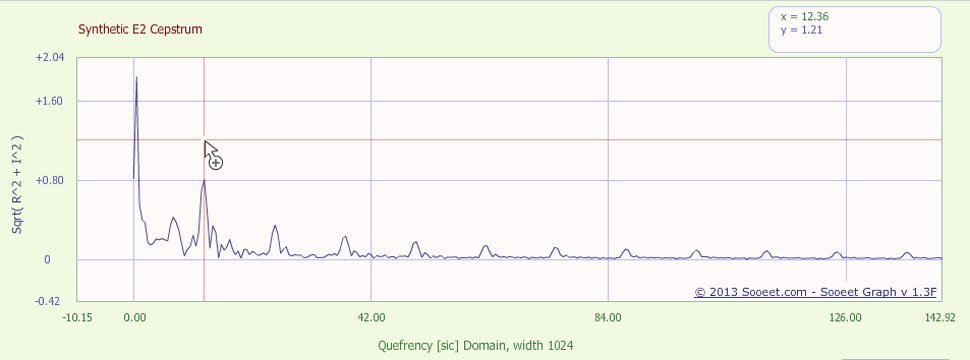
На графике ниже показан Cepstrum синтетической стационарной ноты E2, синтезированной с использованием типичного компонента, близкого к постоянному току, основного тона при 82,4 Гц и 8 гармоник при целых кратных 82,4 Гц. Синтетическая синусоида была запрограммирована для генерации 4096 образцов.

Соблюдайте заметный пик без постоянного тока в 12,36. Ширина Cepstrum равна 1024 (выход второго БПФ), поэтому пик соответствует 1024/12,36 = 82,8 Гц, что очень близко к 82,4 Гц истинной основной частоте.

Теперь давайте рассмотрим настоящий слуховой сигнал.

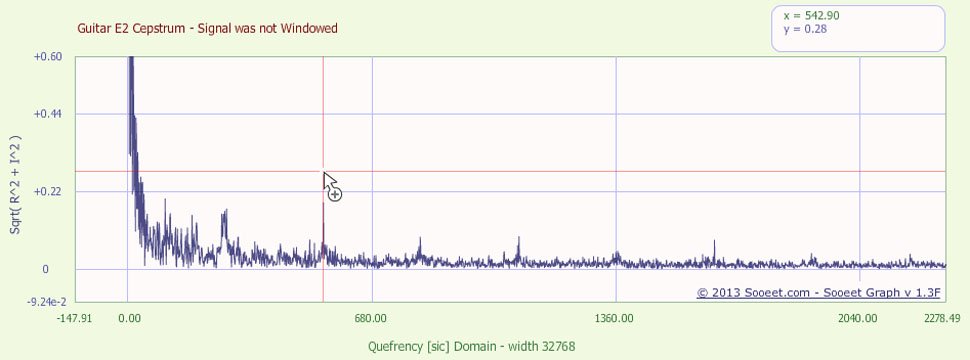
График ниже показывает Cepstrum реальной ноты E2 для акустической гитары. Сигнал не был оконным до первого БПФ. Соблюдайте заметный пик без постоянного тока на 542,9. Ширина Cepstrum равна 32768 (выход второго БПФ), поэтому пик соответствует 32768/542,9 = 60,4 Гц, что довольно далеко от 82,4 Гц истинной основной частоты.

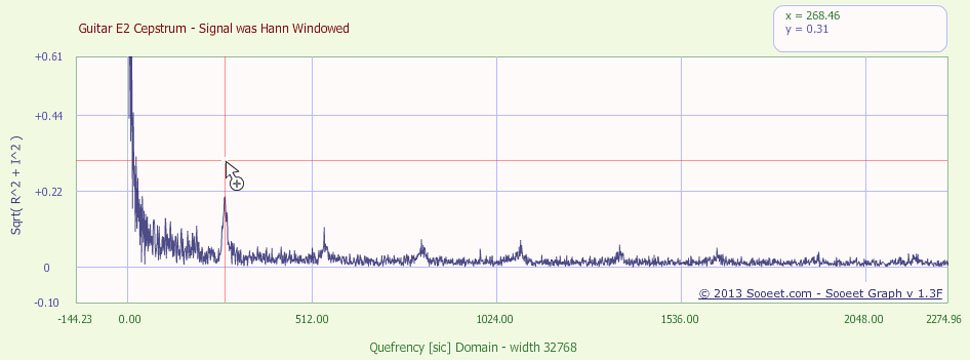
На графике ниже показан Cepstrum той же ноты E2, что и на настоящей акустической гитаре, но на этот раз сигнал был обработан Ханном до первого FFT. Соблюдайте заметный пик без постоянного тока на 268,46. Ширина Cepstrum равна 32768 (выход второго БПФ), поэтому пик соответствует 32768/268,46 = 122,1 Гц, что еще дальше от 82,4 Гц истинной основной частоты.

Нота E2 для акустической гитары, использованная для этого анализа, была взята на частоте 44,1 кГц с помощью высококачественного микрофона в студийных условиях, она практически не содержит фонового шума, никаких других инструментов или голосов и никакой постобработки.

Это иллюстрирует значительную проблему использования Cepstral анализа для определения высоты звука в реальных акустических сигналах.

Рекомендации:

Реальные данные аудиосигнала, генерация синтетического сигнала, графики, БПФ и Cepstral анализ были сделаны здесь: Кепстр музыкального инструмента

Answer 3

Что не так с вашей существующей техникой, что вы заинтересованы в новой? Я не думаю, что кепстр даст вам более точную высоту звука, если это цель. Это, однако, поможет вам с подавленными основами. Я полагаю, что вы могли бы использовать кепстр, чтобы приблизить вас, а затем вернуться к первому БПФ (которое я бы сохранил в его первоначальном виде), а затем применить свою хитрую технику к корзине, к которой ведет вас кепстр.

Что касается квадратичной аппроксимации, это упоминается в этой статье Теда Ноултона, которая недавно возникла в другом SO-вопросе, но я никогда не использовал его.

Я должен добавить, что техника квадратичного подбора, по крайней мере, как указано в справке от Knowlton, зависит от использования прямоугольного окна на первом БПФ. Как объяснил Пол Р. в другом из ваших вопросов, если вы выполняете обработку звука, вы должны использовать окно Ханна или Хемминга на первом БПФ. Поэтому я думаю, что общий алгоритм может выглядеть так:

• Возьмите буфер временной области x, сделайте оконную копию w,
• Sx = FFT(x), Sw = FFT(w)
• c = Log of square magnitude of Sw
• Cx = FFT(c)
• Оцените фундаментальные (и, возможно, гармонические), используя Cx
• использование Sw сделать хитрый фазовый трюк на базовых (или высших гармонических) бинах
• И / или использовать Sx сделать квадратичный бин в соответствии с основной (или более высокой гармоникой)

(or higher harmonic) Примечание применяется, если у вас действительно есть подавленные основы.

И я упоминал об этом в вашем другом вопросе, но с чего вы взяли, что журнал требует таблицы поиска? Почему бы просто не вызвать функцию журнала? Я полагаю, что время, затрачиваемое двумя FFT (O(n*logn)), затмевает любую другую обработку, которую вы можете выполнить.

Answer 4

Анализ кепстра - это форма гомоморфной обработки, описанная в книге Оппенхайма и Шафера "Обработка сигналов с дискретным временем". Когда-то это считалось полезным для отделения частоты возбудителя от огибающей формента (возможно, до сих пор, не знаю). Кажется, это работает лучше, когда дано довольно длинное окно стационарных данных.

Но Cepstral анализ не предназначен для точности оценки частоты. Это на самом деле форма анализа с потерями. Но это может быть полезно при нахождении основной частоты из последовательности гармоник, где спектральная составляющая основной частоты может быть сравнительно слабой или даже отсутствовать.

Анализ фазового вокодера (не такой хитрый, как метод, существующий уже около полувека) лучше подходит для оценки частоты для данного пика, при условии, что вы выбрали правильный пик (не обязательно самый сильный), спектр пика является постоянным и кадры БПФ, и основа не полностью отсутствуют в спектре.

Квадратичная или параболическая интерполяция может подойти, если преобразование вашей оконной функции напоминает параболу. Sinc интерполяция работает лучше с прямоугольными окнами.

Answer 5

Этот ответ предназначен для чтения в дополнение к посту Джереми Сальвена, а также для ответа на вопрос о литературе.

Прежде всего важно рассмотреть, какова периодичность сигнала. Является ли сигнал ближе к полностью периодическому сигналу для данного окна анализа.

Обратитесь сюда для подробного объяснения термина и математики https://en.wikipedia.org/wiki/Almost_periodic_function

Короткий ответ заключается в том, что если для данного окна анализа сигнал является полностью периодическим, или если сигнал является квазипериодическим, а окно анализа является достаточно маленьким, чтобы периодичность была достигнута, то для выполнения задачи достаточно автокорреляции. Примеры сигналов, которые удовлетворяют этим условиям:

• Чистый синусоидальный тон
• Струнные инструменты с длинными сустейнами и стабильным тоном (без вибрато), особенно верно для сустейн-части, не так верно для переходных процессов.
• Духовые инструменты, которые дуют достаточно долго.

Пример сигналов, которые не соответствуют этим условиям:

• Ударные звуки
• Струнные или духовые инструменты, играемые с каждой нотой, держатся очень коротко или меняются в течение короткого времени
• Сложная музыка, или в основном комбинация нескольких инструментов, на которых играют с разными тонами.

Для определения высоты тона с использованием автокорреляции есть руководство по его реализации в Praat:

• http://www.pinguinorodriguez.cl/blog/pitch-in-praat/ Pitch in Praat Краткое описание алгоритма определения высоты звука Praat. Это описывает алгоритм с именем "AC".
• www.fon.hum.uva.nl/paul/praat.html Точный краткосрочный анализ основной частоты и отношения гармоник к шуму дискретизированного звука. Пол Бурсма IFA Proceedings 17: 97-110.

В документе подробно описывается использование несмещенной автокорреляции (термин, используемый Джереми Сальвеном) для обнаружения основного тона, а также показано, что он превосходит смещенную автокорреляцию для обнаружения основного тона. Хотя он отмечает, что результаты автокорреляции имеют значение только для половины размера окна, вы не должны рассчитывать вторую половину.

Предвзятая автокорреляция выполняется путем оконного преобразования сигналов с использованием сужающегося окна, а затем выполняется автокорреляция. Это уменьшает влияние низкочастотной модуляции (изменение амплитуды в медленном масштабе времени), которая наносит ущерб обнаружению основного тона, поскольку в противном случае части с большей амплитудой будут давать больший коэффициент автокорреляции, который будет предпочтительным.

Алгоритм, используемый в работе Бурсмы, может быть описан в 5 шагов:

1. Удалить DC из сигнала, который собирается быть оконным (x - x_avg)
2. Окно сигнала, используя функцию конусности (он утверждает, что для него используется окно Ханна, или, лучше, гауссово окно)
3. Автокоррелирует сигнал
4. Разделите автокорреляционную функцию на автокорреляцию используемого окна.
5. Выбор пика (аналогично предыдущим алгоритмам)

Важно отметить, что окно будет стремиться к нулю на обоих концах, и автокорреляция окна также будет стремиться к нулю. Вот почему вторая половина несмещенной автокорреляции бесполезна, это деление на ноль, приближающееся к концу окна.

Далее идет Инь: - Де Шевинье, Ален и Хидеки Кавахара. "Инь, фундаментальный частотный оценщик речи и музыки". Журнал Акустического общества Америки 111,4 (2002): 1917-1930.

Насколько я понимаю, статья YIN также свидетельствует о том, что использование конусного окна отрицательно влияет на точность определения высоты тона. И что интересно, он предпочитает не использовать какую-либо функцию сужающегося окна (это говорит о том, что сужающееся окно не приносит каких-либо улучшений в результаты и вместо этого усложняет это).

Последними являются SNAC и WSNAC Филиппа МакЛауда (уже связанные Джереми Салвеном):

• Philip McLeod, Быстрые, точные инструменты определения высоты звука для анализа музыки, кандидатская диссертация, факультет компьютерных наук, Университет Отаго, 2008.
• Маклеод. P, Wyvill. G, "Разумный способ найти поле", учеб. Международная конференция по компьютерной музыке, Барселона, Испания, 5-9 сентября 2005 г., с. 138-141.
• Маклеод. P, Wyvill. G, "Визуализация музыкального поля", учеб. Computer Graphics International, Токио, Япония, 9-11 июля 2003 г., стр. 300-303.

Их можно найти по адресу miracle.otago.ac.nz/tartini/papers.html.

Я не слишком углубился в это, но есть упоминание о нем как о методе уменьшения вредного воздействия сужающегося окна смещенной автокорреляции, которое отличается от метода, используемого Boersma. (обратите внимание, что я ничего не слышал о MPM, поэтому ничего не могу сказать по этому поводу)

Последнее предложение заключается в том, что если вы создаете инструментальный тюнер, способ, который будет проще и даст немного лучший результат по сравнению с автокорреляцией, заключается в использовании взаимной корреляции с чистым синусоидальным сигналом с заранее определенной частотой.

Джереми Салвен:

То есть предположим, что вы построили функцию sin(4x)+sin(6x)+sin(8x)+sin(10x). Если вы посмотрите на это, то ясно, что оно имеет ту же частоту, что и функция sin(2x). Однако, если вы примените к этой функции анализ Фурье, ячейка, соответствующая sin(2x), будет иметь нулевую величину. Таким образом, считается, что этот сигнал имеет "отсутствующую основную частоту", потому что он не содержит синусоиды частоты, которой мы считаем ее.

Я хотел бы доказать, что хотя данный сигнал является периодическим при \ omega = 2, он не совпадает с частотой, равной функции sin(2x). Как показывает анализ Фурье, компонент sin (2x) имеет нулевую величину. Это связано с тем, что существует связь между высотой тона, частотой и основной частотой сигнала, но они различны и не взаимозаменяемы. Важно помнить, что высота звука является субъективным измерением, что она зависит от человека как человека, который его воспринимает. Похоже, что он имеет ту же частоту, что и грех (2х), именно так мы воспринимаем это визуально. Тот же эффект также происходит аналогичным образом в отношении восприятия высоты звука и звука. Пример, который сразу пришел в голову, - это "Удары", то есть воспринимаемая высота звука, которая слышна, когда есть две синусоидальные волны с близкими, но разными частотами.