Запросы, чтобы выяснить, лежит ли точка внутри многоугольника

Question

Мне дали строго выпуклый многоугольник из S сторон и Q запросов для обработки.

Все точки многоугольника и точки запроса задаются парами (x,y). Точки многоугольника задаются против часовой стрелки.

Вышеупомянутые переменные ограничены так, что 1<=S<=10^6 а также 1<=Q<=10^5 а также 1<=|x|,|y|<=10^9,

Для каждого запроса я должен вывести "Да", если данная точка лежит внутри многоугольника; иначе нет

Я попытался использовать тест на включение O(S) (приведение к лучам), и он оказался тайм-аут для больших тестовых случаев, но также не прошел все предварительные тесты.

Очевидно, что реализация не охватывала все крайние случаи, и я узнал о конкретном алгоритме для этого вопроса, который мог бы ответить на каждый запрос в O(log S) с помощью бинарного поиска, но я не могу понять, как реализовать его из псевдокод (впервые занимаюсь вычислительной геометрией).

Может ли кто-нибудь предоставить мне алгоритм, который охватывает все крайние случаи в пределах требуемой сложности времени (Q log S), или направить меня на страницу или статью, в которой он реализован?

Answer 1

Вы можете сделать алгоритм сканирования линии. Вам нужно отсортировать точки Q по их координате x. Затем найдите точку S с самым низким значением x и рассмотрите линию, движущуюся вдоль оси x. Вам нужно отследить две стороны многоугольника.

Затем двигайтесь вдоль многоугольника и установите Q в возрастающей координате x. Для каждой точки вам просто нужно проверить, находится ли она между двумя линиями, которые вы отслеживаете.

Сложность равна O(Q logQ + S), если Q не отсортирован, и O(Q+S), если Q уже отсортирован.

Answer 2

Во-первых, вы можете разбить выпуклый многоугольник на левую и правую части, начиная с верхней точки и заканчивая нижней. Точки в обеих частях уже отсортированы по yкоордината.

Предположим, что точка запроса имеет координаты (qx, qy), Теперь вы можете попытаться найти (используя бинарный поиск) сегмент из левой части и сегмент из правой части, которые пересекаются с линией y = qy, Если бы вы могли найти оба сегмента и qx лежит между x-координаты пересечений отрезков с линией y = qyэто внутри многоугольника.

Сложность запроса O(log(S)),

Answer 3

Нет необходимости сортировать, выпуклый многоугольник уже отсортирован!

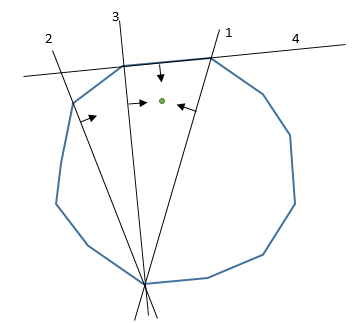
Для выпуклого многоугольника расположение точки быстро и просто: разбейте многоугольник на две части, используя прямую линию между вершиной 0 и вершиной S/2. Подписанный тест области скажет вам, на какой стороне находится контрольная точка, а какую половину оставить (половина также является выпуклым многоугольником).

Продолжить рекурсивно до S=3 и сравнения с опорной линией третьей стороны.

O (Log (S)) тестов всего за запрос.

(Числа показывают порядок разбиений.)