Неожиданные результаты БПФ с Python

Question

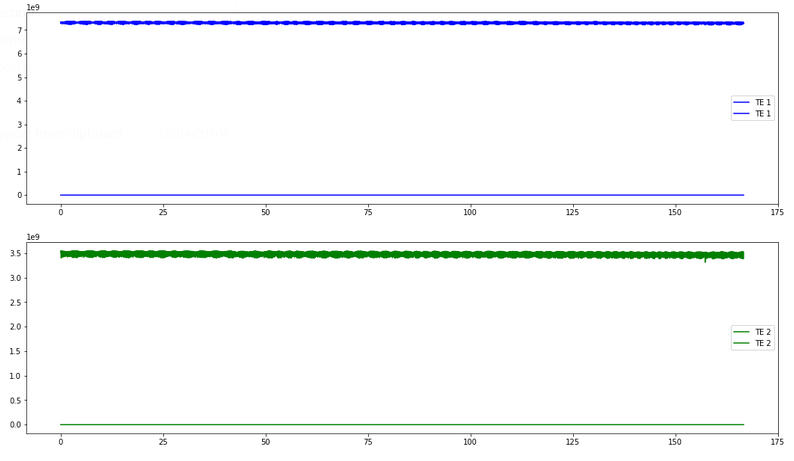
Я анализирую то, что по сути является дыхательной формой волны, построенной в 3 различных формах (данные получены из МРТ, поэтому использовалось многократное время эхо-сигнала; посмотрите здесь, если вам нужен какой-то быстрый фон). Вот пара сегментов двух из построенных кривых для некоторого контекста:

Для каждого сигнала я пытаюсь выполнить ДПФ, чтобы обнаружить доминирующую частоту или частоты дыхания.

Моя проблема заключается в том, что когда я строю выполняемые мной ДПФ, я получаю одну из двух вещей, в зависимости от используемой библиотеки БПФ. Кроме того, ни один из них не является представителем того, что я ожидаю. Я понимаю, что данные не всегда выглядят так, как мы хотим, но у меня явно присутствуют осциллограммы в моих данных, поэтому я ожидаю, что дискретное преобразование Фурье приведет к пику частоты где-то разумно. Для справки здесь я бы ожидал около 80-130 Гц.

Мои данные хранятся в pandas фрейм данных, с данными каждого эхо-времени в отдельной серии. Я применяю выбранную функцию FFT (см. Код ниже) и получаю разные результаты для каждого из них.

SciPy (fftpack)

import pandas as pd
import scipy.fftpack

# temporary copy to maintain data structure
lead_pts_fft_df = lead_pts_df.copy()

# apply a discrete fast Fourier transform to each data series in the data frame
lead_pts_fft_df.magnitude = lead_pts_df.magnitude.apply(scipy.fftpack.fft)
lead_pts_fft_df

NumPy:

import pandas as pd
import numpy as np 

# temporary copy to maintain data structure
lead_pts_fft_df = lead_pts_df.copy()

# apply a discrete fast Fourier transform to each data series in the data frame
lead_pts_fft_df.magnitude = lead_pts_df.magnitude.apply(np.fft.fft)
lead_pts_fft_df

Остальная часть соответствующего кода:

ECHO_TIMES = [0.080, 0.200, 0.400] # milliseconds

f_s = 1 / (0.006) # 0.006 = time between samples
freq = np.linspace(0, 29556, 29556) * (f_s / 29556) # (29556 = length of data)

# generate subplots
fig, axes = plt.subplots(3, 1, figsize=(18, 16))

for idx in range(len(ECHO_TIMES)):
    axes[idx].plot(freq, lead_pts_fft_df.magnitude[idx].real, # real part
                   freq, lead_pts_fft_df.magnitude[idx].imag, # imaginary part

    axes[idx].legend() # apply legend to each set of axes

# show the plot
plt.show()

Post-DFT (SciPy fftpack):

Post-DFT (NumPy)

Вот ссылка на набор данных (в Dropbox), использованный для создания этих графиков, а также ссылка на Блокнот Jupyter.

РЕДАКТИРОВАТЬ:

Я использовал опубликованный совет и взял величину (абсолютное значение) данных, а также построил график с логарифмической осью Y. Новые результаты размещены ниже. Похоже, что у меня есть некоторый поворот в моем сигнале. Я не использую правильную частотную шкалу? Обновленный код и графики приведены ниже.

# generate subplots
fig, axes = plt.subplots(3, 1, figsize=(18, 16))

for idx in range(len(ECHO_TIMES)):
    axes[idx].plot(freq[1::], np.log(np.abs(lead_pts_fft_df.magnitude[idx][1::])),
                   label=lead_pts_df.index[idx], # apply labels
                   color=plot_colors[idx]) # colors
    axes[idx].legend() # apply legend to each set of axes

# show the plot
plt.show()

Answer 1

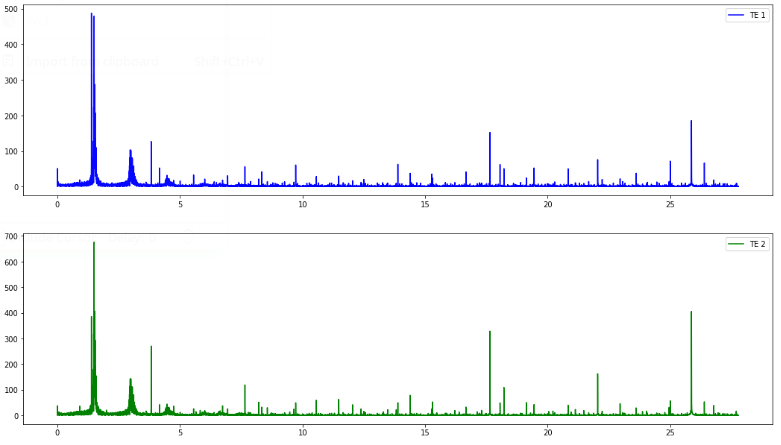
Я выяснил свои проблемы.

Cris Luengo очень помог с этой ссылкой, которая помогла мне определить, как правильно масштабировать мои частотные интервалы и правильно построить DFT.

ДОПОЛНИТЕЛЬНО: я забыл принять во внимание смещение, присутствующее в сигнале. Это не только вызывает проблемы с огромным пиком при 0 Гц в DFT, но также является причиной большей части шума в преобразованном сигнале. Я использовал scipy.signal.detrend() чтобы устранить это и получил очень подходящий вид DFT.

# import DFT and signal packages from SciPy
import scipy.fftpack
import scipy.signal

# temporary copy to maintain data structure; original data frame is NOT changed due to ".copy()"
lead_pts_fft_df = lead_pts_df.copy()

# apply a discrete fast Fourier transform to each data series in the data frame AND detrend the signal
lead_pts_fft_df.magnitude = lead_pts_fft_df.magnitude.apply(scipy.signal.detrend)
lead_pts_fft_df.magnitude = lead_pts_fft_df.magnitude.apply(np.fft.fft)
lead_pts_fft_df

Расположите ячейки частоты соответственно:

num_projections = 29556
N = num_projections
T = (6 * 3) / 1000 # 6*3 b/c of the nature of my signal: 1 pt for each waveform collected every third acquisition
xf = np.linspace(0.0, 1.0 / (2.0 * T), num_projections / 2)

Тогда сюжет:

# generate subplots
fig, axes = plt.subplots(3, 1, figsize=(18, 16))

for idx in range(len(ECHO_TIMES)):
    axes[idx].plot(xf, 2.0/num_projections * np.abs(lead_pts_fft_df.magnitude[idx][:num_projections//2]),
                   label=lead_pts_df.index[idx], # apply labels
                   color=plot_colors[idx]) # colors
    axes[idx].legend() # apply legend to each set of axes

# show the plot
plt.show()