Построение быстрого преобразования Фурье в Python

Question

У меня есть доступ к NumPy и Scipy и хочу создать простой БПФ из набора данных. У меня есть два списка, один из которых представляет собой значения y, а другой - метки времени для этих значений y.

Какой самый простой способ подать эти списки в метод scipy или numpy и построить результирующее FFT?

Я посмотрел примеры, но все они основаны на создании набора фальшивых данных с некоторым определенным количеством точек данных, частотой и т. Д., И на самом деле не показывают, как это сделать, используя только набор данных и соответствующие временные метки.,

Я попробовал следующий пример:

from scipy.fftpack import fft
# Number of samplepoints
N = 600
# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N)
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = fft(y)
xf = np.linspace(0.0, 1.0/(2.0*T), N/2)
import matplotlib.pyplot as plt
plt.plot(xf, 2.0/N * np.abs(yf[0:N/2]))
plt.grid()
plt.show()

Но когда я изменяю аргумент fft на свой набор данных и строю его, я получаю очень странные результаты, кажется, что масштабирование частоты может быть отключено. я не уверен

Вот пастбин данных, которые я пытаюсь БПФ

http://pastebin.com/0WhjjMkb http://pastebin.com/ksM4FvZS

Когда я делаю FFT для всего этого, он просто имеет огромный всплеск в ноль и ничего больше

Вот мой код:

## Perform FFT WITH SCIPY
signalFFT = fft(yInterp)

## Get Power Spectral Density
signalPSD = np.abs(signalFFT) ** 2

## Get frequencies corresponding to signal PSD
fftFreq = fftfreq(len(signalPSD), spacing)

## Get positive half of frequencies
i = fftfreq>0

##
plt.figurefigsize=(8,4));
plt.plot(fftFreq[i], 10*np.log10(signalPSD[i]));
#plt.xlim(0, 100);
plt.xlabel('Frequency Hz');
plt.ylabel('PSD (dB)')

расстояние просто равно xInterp[1]-xInterp[0]

Answer 1

Итак, я запускаю функционально эквивалентную форму вашего кода в блокноте IPython:

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack

# Number of samplepoints
N = 600
# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N)
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = scipy.fftpack.fft(y)
xf = np.linspace(0.0, 1.0/(2.0*T), N/2)

fig, ax = plt.subplots()
ax.plot(xf, 2.0/N * np.abs(yf[:N//2]))
plt.show()

Я получаю то, что считаю очень разумным выходом.

Прошло больше времени, чем я хотел бы признать, с тех пор как я учился в инженерной школе и думал об обработке сигналов, но скачки в 50 и 80 - это именно то, чего я ожидал. Так в чем же проблема?

В ответ на необработанные данные и публикуемые комментарии

Проблема здесь в том, что у вас нет периодических данных. Вы должны всегда проверять данные, которые вы вводите в любой алгоритм, чтобы убедиться, что он уместен.

import pandas
import matplotlib.pyplot as plt
#import seaborn
%matplotlib inline

# the OP's data
x = pandas.read_csv('http://pastebin.com/raw.php?i=ksM4FvZS', skiprows=2, header=None).values
y = pandas.read_csv('http://pastebin.com/raw.php?i=0WhjjMkb', skiprows=2, header=None).values
fig, ax = plt.subplots()
ax.plot(x, y)

Answer 2

Важной особенностью fft является то, что его можно применять только к данным, в которых временная метка является однородной (т. Е. Равномерная выборка по времени, как показано выше).

В случае неравномерной выборки, пожалуйста, используйте функцию для подбора данных. Есть несколько уроков и функций на выбор:

https://github.com/tiagopereira/python_tips/wiki/Scipy%3A-curve-fitting http://docs.scipy.org/doc/numpy/reference/generated/numpy.polyfit.html

Если подгонка не является опцией, вы можете напрямую использовать некоторую форму интерполяции для интерполяции данных в единую выборку:

https://docs.scipy.org/doc/scipy-0.14.0/reference/tutorial/interpolate.html

Когда у вас есть единообразные образцы, вам придется беспокоиться только о дельте времени (t[1] - t[0]) ваших образцов. В этом случае вы можете напрямую использовать функции FFT

Y    = numpy.fft.fft(y)
freq = numpy.fft.fftfreq(len(y), t[1] - t[0])

pylab.figure()
pylab.plot( freq, numpy.abs(Y) )
pylab.figure()
pylab.plot(freq, numpy.angle(Y) )
pylab.show()

Это должно решить вашу проблему.

Answer 3

Мне нужно создать функцию, которая занимается построением БПФ реальных сигналов. В моей функции есть АКТУАЛЬНАЯ амплитуда сигнала (опять же, из-за предположения о реальном сигнале, что означает симметрию...):

import matplotlib.pyplot as plt
import numpy as np
import warnings

def fftPlot(sig, dt=None, block=False, plot=True):
    # here it's assumes analytic signal (real signal...)- so only half of the axis is required

    if dt is None:
        dt = 1
        t = np.arange(0, sig.shape[-1])
        xLabel = 'samples'
    else:
        t = np.arange(0, sig.shape[-1]) * dt
        xLabel = 'freq [Hz]'

    if sig.shape[0] % 2 != 0:
        warnings.warn("signal prefered to be even in size, autoFixing it...")
        t = t[0:-1]
        sig = sig[0:-1]

    sigFFT = np.fft.fft(sig) / t.shape[0]  # divided by size t for coherent magnitude

    freq = np.fft.fftfreq(t.shape[0], d=dt)

    # plot analytic signal - right half of freq axis needed only...
    firstNegInd = np.argmax(freq < 0)
    freqAxisPos = freq[0:firstNegInd]
    sigFFTPos = 2 * sigFFT[0:firstNegInd]  # *2 because of magnitude of analytic signal

    if plot:
        plt.figure()
        plt.plot(freqAxisPos, np.abs(sigFFTPos))
        plt.xlabel(xLabel)
        plt.ylabel('mag')
        plt.title('Analytic FFT plot')
        plt.show(block=block)

    return sigFFTPos, freqAxisPos


if __name__ == "__main__":
    dt = 1 / 1000
    f0 = 1 / dt / 4

    t = np.arange(0, 1 + dt, dt)
    sig = np.sin(2 * np.pi * f0 * t)
    fftPlot(sig, dt=dt)
    fftPlot(sig)

    t = np.arange(0, 1 + dt, dt)
    sig = np.sin(2 * np.pi * f0 * t) + 10 * np.sin(2 * np.pi * f0 / 2 * t)
    fftPlot(sig, dt=dt, block=True)

Answer 4

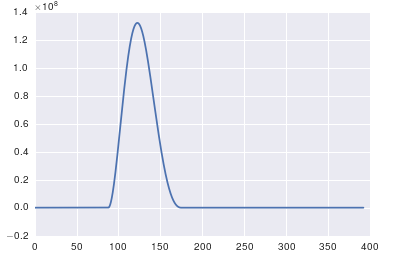
Высокий всплеск, который у вас есть, связан с DC (неизменяемой, т.е. freq = 0) частью вашего сигнала. Это проблема масштаба. Если вы хотите просматривать содержимое, не относящееся к постоянному току, для визуализации вам может потребоваться построить график от смещения 1, а не от смещения 0 БПФ сигнала.

Изменение приведенного выше примера @PaulH

import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack

# Number of samplepoints
N = 600
# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N)
y = 10 + np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = scipy.fftpack.fft(y)
xf = np.linspace(0.0, 1.0/(2.0*T), N/2)

plt.subplot(2, 1, 1)
plt.plot(xf, 2.0/N * np.abs(yf[0:N/2]))
plt.subplot(2, 1, 2)
plt.plot(xf[1:], 2.0/N * np.abs(yf[0:N/2])[1:])

Выходные участки: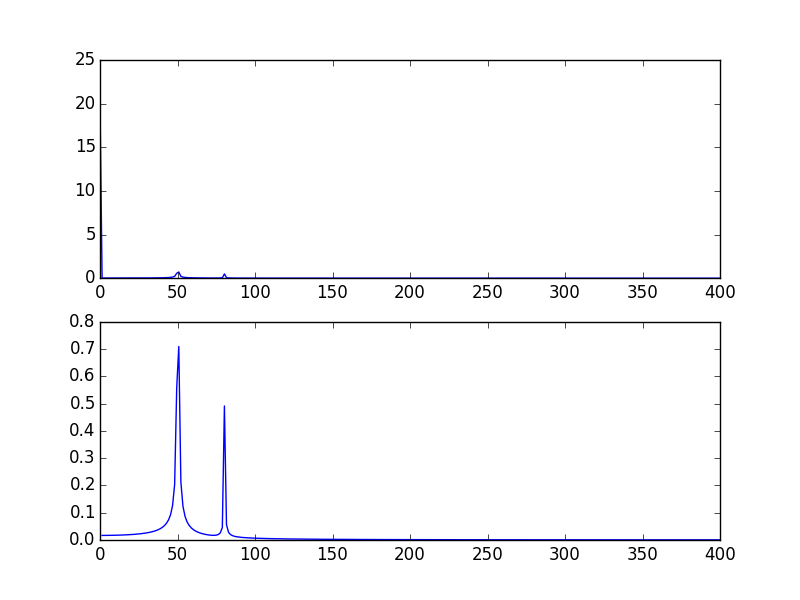

Другой способ - визуализировать данные в логарифмическом масштабе:

С помощью:

plt.semilogy(xf, 2.0/N * np.abs(yf[0:N/2]))

Покажет: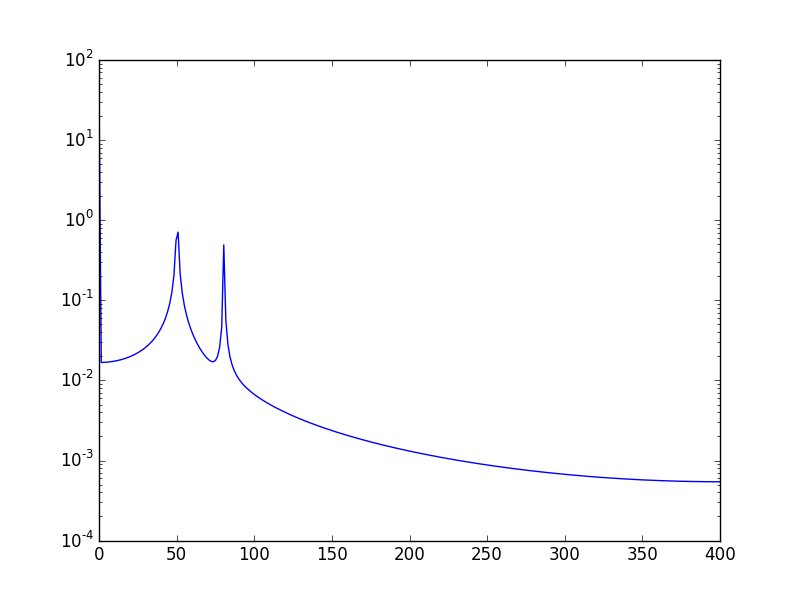

Answer 5

В качестве дополнения к уже приведенным ответам, я хотел бы отметить, что часто важно играть с размерами ячеек для БПФ. Было бы целесообразно протестировать набор значений и выбрать тот, который имеет больше смысла для вашего приложения. Часто это в той же величине количество образцов. Это было принято большинством данных ответов и дает отличные и разумные результаты. В случае, если кто-то хочет исследовать это, вот моя версия кода:

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack

fig = plt.figure(figsize=[14,4])
N = 600           # Number of samplepoints
Fs = 800.0
T = 1.0 / Fs      # N_samps*T (#samples x sample period) is the sample spacing.
N_fft = 80        # Number of bins (chooses granularity)
x = np.linspace(0, N*T, N)     # the interval
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)   # the signal

# removing the mean of the signal
mean_removed = np.ones_like(y)*np.mean(y)
y = y - mean_removed

# Compute the fft.
yf = scipy.fftpack.fft(y,n=N_fft)
xf = np.arange(0,Fs,Fs/N_fft)

##### Plot the fft #####
ax = plt.subplot(121)
pt, = ax.plot(xf,np.abs(yf), lw=2.0, c='b')
p = plt.Rectangle((Fs/2, 0), Fs/2, ax.get_ylim()[1], facecolor="grey", fill=True, alpha=0.75, hatch="/", zorder=3)
ax.add_patch(p)
ax.set_xlim((ax.get_xlim()[0],Fs))
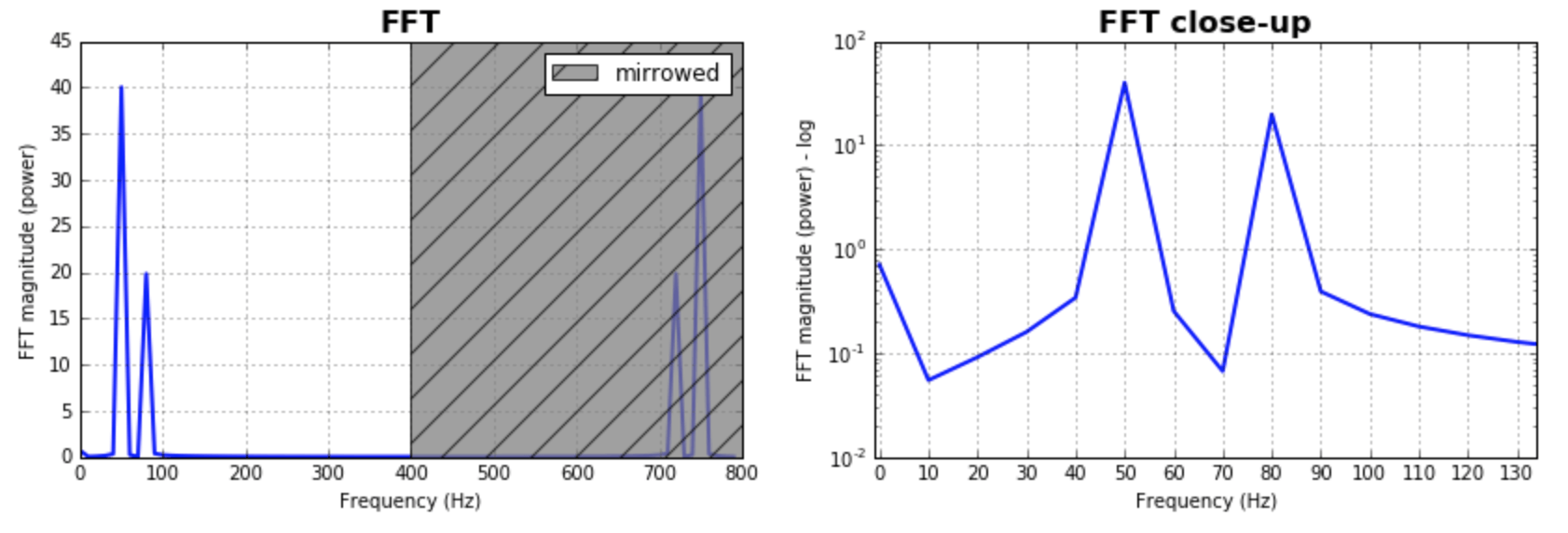
ax.set_title('FFT', fontsize= 16, fontweight="bold")
ax.set_ylabel('FFT magnitude (power)')
ax.set_xlabel('Frequency (Hz)')
plt.legend((p,), ('mirrowed',))
ax.grid()

##### Close up on the graph of fft#######
# This is the same histogram above, but truncated at the max frequence + an offset. 
offset = 1    # just to help the visualization. Nothing important.
ax2 = fig.add_subplot(122)
ax2.plot(xf,np.abs(yf), lw=2.0, c='b')
ax2.set_xticks(xf)
ax2.set_xlim(-1,int(Fs/6)+offset)
ax2.set_title('FFT close-up', fontsize= 16, fontweight="bold")
ax2.set_ylabel('FFT magnitude (power) - log')
ax2.set_xlabel('Frequency (Hz)')
ax2.hold(True)
ax2.grid()

plt.yscale('log')

выходные участки:

Answer 6

Я пишу этот дополнительный ответ, чтобы объяснить происхождение распространения всплесков при использовании fft, и особенно обсуждаю руководство scipy.fftpack, с которым я в какой-то момент не согласен.

В этом примере время записи tmax=N*T=0.75. Сигналsin(50*2*pi*x)+0.5*sin(80*2*pi*x). Частотный сигнал должен содержать 2 пика на частотах50 а также 80 с амплитудами 1 а также 0.5. Однако, если анализируемый сигнал не имеет целого числа периодов, диффузия может появиться из-за усечения сигнала:

• Щука 1: 50*tmax=37.5 => частота 50 не является кратным 1/tmax=> Наличие диффузии из-за усечения сигнала на этой частоте.
• Щука 2: 80*tmax=60 => частота 80 кратно 1/tmax=> Нет диффузии из-за усечения сигнала на этой частоте.

Вот код, который анализирует тот же сигнал, что и в учебнике (sin(50*2*pi*x)+0.5*sin(80*2*pi*x)), но с небольшими отличиями:

1. Исходный пример scipy.fftpack.
2. Исходный пример scipy.fftpack с целым числом периодов сигнала (tmax=1.0 вместо того 0.75 чтобы избежать распространения усечения).
3. Исходный пример scipy.fftpack с целым числом периодов сигнала, а даты и частоты взяты из теории БПФ.

Код:

import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack

# 1. Linspace
N = 600
# sample spacing
tmax = 3/4
T = tmax / N # =1.0 / 800.0
x1 = np.linspace(0.0, N*T, N)
y1 = np.sin(50.0 * 2.0*np.pi*x1) + 0.5*np.sin(80.0 * 2.0*np.pi*x1)
yf1 = scipy.fftpack.fft(y1)
xf1 = np.linspace(0.0, 1.0/(2.0*T), N//2)

# 2. Integer number of periods
tmax = 1
T = tmax / N # sample spacing
x2 = np.linspace(0.0, N*T, N)
y2 = np.sin(50.0 * 2.0*np.pi*x2) + 0.5*np.sin(80.0 * 2.0*np.pi*x2)
yf2 = scipy.fftpack.fft(y2)
xf2 = np.linspace(0.0, 1.0/(2.0*T), N//2)

# 3. Correct positionning of dates relatively to FFT theory (arange instead of linspace)
tmax = 1
T = tmax / N # sample spacing
x3 = T * np.arange(N)
y3 = np.sin(50.0 * 2.0*np.pi*x3) + 0.5*np.sin(80.0 * 2.0*np.pi*x3)
yf3 = scipy.fftpack.fft(y3)
xf3 = 1/(N*T) * np.arange(N)[:N//2]

fig, ax = plt.subplots()
# Plotting only the left part of the spectrum to not show aliasing
ax.plot(xf1, 2.0/N * np.abs(yf1[:N//2]), label='fftpack tutorial')
ax.plot(xf2, 2.0/N * np.abs(yf2[:N//2]), label='Integer number of periods')
ax.plot(xf3, 2.0/N * np.abs(yf3[:N//2]), label='Correct positionning of dates')
plt.legend()
plt.grid()
plt.show()

Выход:

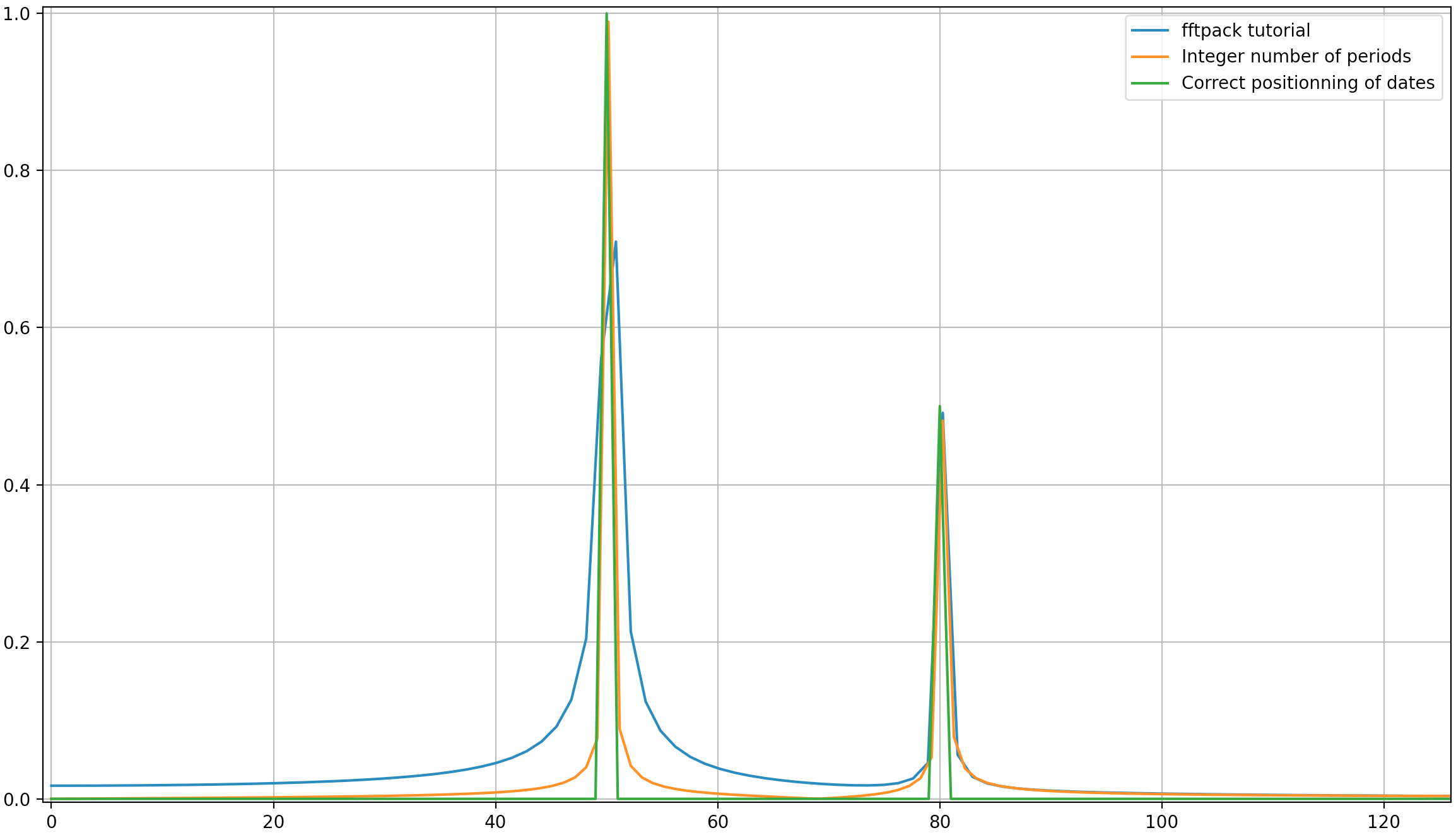
Как это может быть здесь, даже при использовании целого числа периодов некоторая диффузия все же остается. Такое поведение связано с неправильным расположением дат и частот в учебнике scipy.fftpack. Следовательно, в теории дискретных преобразований Фурье:

• сигнал должен быть оценен по датам t=0,T,...,(N-1)*T где T - период дискретизации, а общая длительность сигнала равна tmax=N*T. Обратите внимание, что мы останавливаемся наtmax-T.
• соответствующие частоты f=0,df,...,(N-1)*df где df=1/tmax=1/(N*T)- частота дискретизации. Все гармоники сигнала должны быть кратны частоте дискретизации, чтобы избежать диффузии.

В приведенном выше примере вы можете видеть, что использование arange вместо того linspaceпозволяет избежать дополнительной диффузии в частотном спектре. Более того, используяlinspace версия также приводит к смещению всплесков, которые расположены на немного более высоких частотах, чем они должны быть, как это видно на первом рисунке, где всплески немного справа от частот. 50 а также 80.

Я просто сделаю вывод, что пример использования следует заменить следующим кодом (который, на мой взгляд, менее вводит в заблуждение):

import numpy as np
from scipy.fftpack import fft
# Number of sample points
N = 600
T = 1.0 / 800.0
x = T*np.arange(N)
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = fft(y)
xf = 1/(N*T)*np.arange(N//2)
import matplotlib.pyplot as plt
plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.grid()
plt.show()

Вывод (второй шип уже не разлетается):

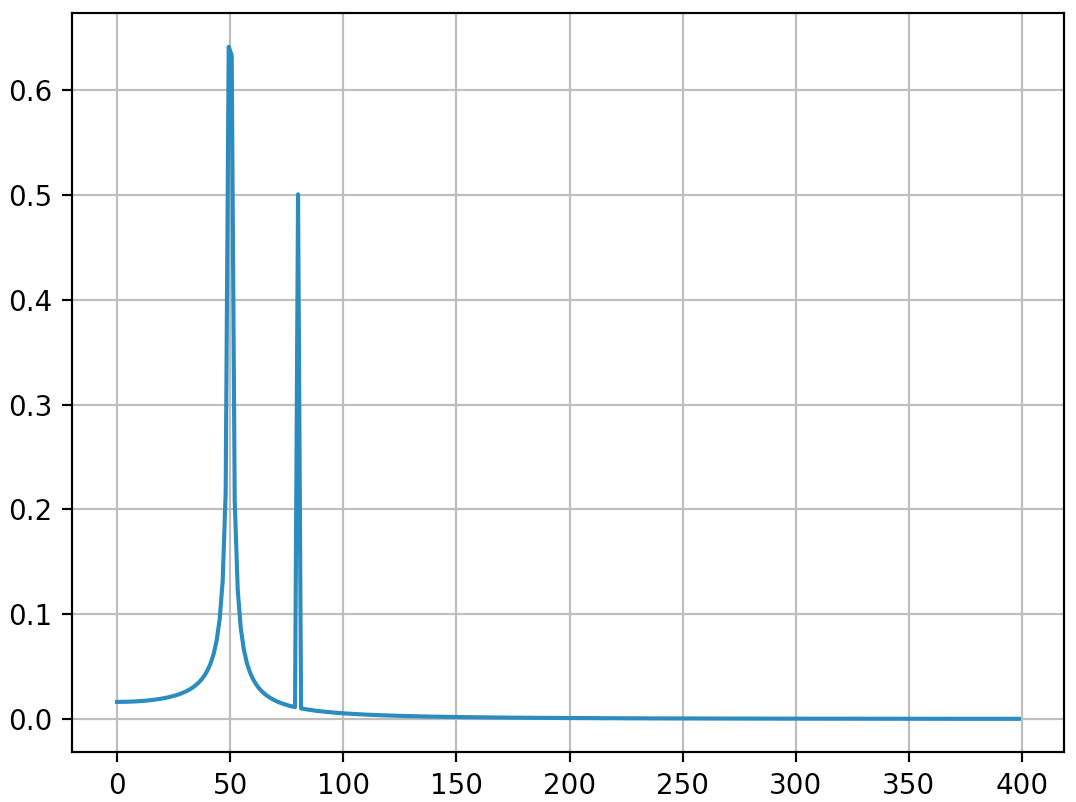
Я думаю, что этот ответ по-прежнему дает некоторые дополнительные объяснения о том, как правильно применять дискретное преобразование Фурье. Очевидно, мой ответ слишком длинный, и всегда есть что сказать (@ewerlopes, например, кратко говорил о псевдониме, и многое можно сказать об оконном режиме), поэтому я остановлюсь. Я думаю, что очень важно глубоко понимать принципы дискретного преобразования Фурье при его применении, потому что мы все знаем, как много людей добавляют факторы здесь и там, применяя его, чтобы получить то, что они хотят.

Answer 7

На этой странице уже есть отличные решения, но все предполагали, что набор данных распределен равномерно / равномерно. Я попытаюсь привести более общий пример случайных выборок данных. Я также буду использовать этот учебник MATLAB в качестве примера:

Добавление необходимых модулей:

import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack
import scipy.signal

Генерация образца данных:

N = 600 # number of samples
t = np.random.uniform(0.0, 1.0, N) # assuming the time start is 0.0 and time end is 1.0
S = 1.0 * np.sin(50.0 * 2 * np.pi * t) + 0.5 * np.sin(80.0 * 2 * np.pi * t) 
X = S + 0.01 * np.random.randn(N) # adding noise

Сортировка набора данных:

order = np.argsort(t)
ts = np.array(t)[order]
Xs = np.array(X)[order]

Resampling:

T = (t.max() - t.min()) / N # average period 
Fs = 1 / T # average sample rate frequency
f = Fs * np.arange(0, N // 2 + 1) / N; # resampled frequency vector
X_new, t_new = scipy.signal.resample(Xs, N, ts)

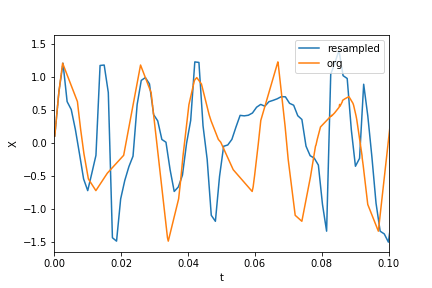
построение графиков данных и данных с повторной выборкой:

plt.xlim(0, 0.1)
plt.plot(t_new, X_new, label="resampled")
plt.plot(ts, Xs, label="org")
plt.legend()
plt.ylabel("X")
plt.xlabel("t")

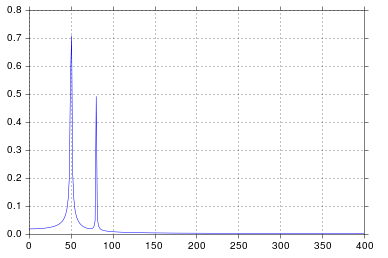
Теперь вычисляем FFT:

Y = scipy.fftpack.fft(X_new)
P2 = np.abs(Y / N)
P1 = P2[0 : N // 2 + 1]
P1[1 : -2] = 2 * P1[1 : -2]

plt.ylabel("Y")
plt.xlabel("f")
plt.plot(f, P1)