Расчет диаграммы Вороного для самолетов в 3D
Существует ли код / библиотека, которая может рассчитать диаграмму Вороного для плоскостей (параллелограммов) в 3D? Я проверил Qhull, и кажется, что он может работать только с точками, в его примерах Voro++ работает с сферами разного размера, но я ничего не мог найти для полигонов.
На этом изображении (образцы плоскостей в 3d) параллелограммы являются трехмерными, поскольку они имеют толщину, но в этом случае толщина будет равна нулю.!
2 ответа
Клетки Вороного не являются параллелограммами. Вы смущены здесь изображением, которое вы разместили. Границы ячейки Вороного являются частями гиперплоскостей, разделяющих отдельные средства.
Посетите этот сайт, где обсуждаются и визуализируются трехмерные диаграммы воронои:
http://www.wblut.com/2009/04/28/ooh-ooh-ooh-3d-voronoi/
Чтобы вычислить клетки вороной, наиболее распространенным способом является сначала построение триангуляции Делоне. Есть несколько алгоритмов, чтобы сделать это в 2D, в то время как в 3D это становится значительно более сложным. Но вы все равно должны быть в состоянии найти что-то. qhull может быть правильный путь.
Когда у вас есть триангуляция Делоне, вычислите центр каждого тетраэдера. Это углы многоугольников, которые вам нужно нарисовать. Для любого ребра в триангуляции Делоне нарисуйте многоугольник, соединяющий соседние центры. Это должна быть гиперплоскость. Теперь все, что вам нужно сделать, это также нарисовать Гиперплоскости для ребер, которые являются частью выпуклой оболочки. Для этого вам нужно продолжить гиперплоскости, которые у вас уже должны быть изнутри до бесконечности снаружи.
Я настоятельно рекомендую начать с 2d в первую очередь. Когда у вас есть рабочий код для 2D, посмотрите, как сделать то же самое в 3D. Это уже довольно сложно в 2D, если вы хотите, чтобы это было быстро.
Это рисунок из Википедии, на котором изображены диаграммы Делоне и Вороного: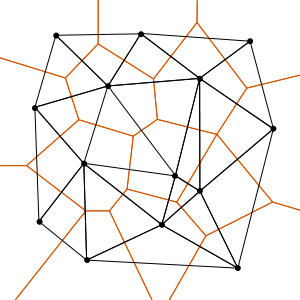
Черные линии - триангуляция Делоне. Коричневые линии ортогональны этому и образуют диаграмму Вороного. Триангуляция Делоне может использоваться для различных интересных задач визуализации: вычисления выпуклой оболочки, диаграмм вороного и альфа-форм: http://www.cgal.org/Manual/latest/doc_html/cgal_manual/Alpha_shapes_3/Chapter_main.html
Боуер-Ватсон обычно является рекомендуемым алгоритмом. Проблема с большинством работ / алгоритмов заключается в том, что они не решают сложные ситуации, возникающие, когда точки находятся близко друг к другу в пространстве (поэтому тетраэдры тонкие), когда клетки вороной должны быть в основном плоскими и когда несколько точек находятся на та же сфера. Добавьте к этому числовую сложность работы с неточной математикой и округлением, и вы получите рецепт бесконечной отладки. Я рекомендую сначала отфильтровать данные, если это приемлемо. В противном случае вы в конечном итоге закодируете огромное количество особых случаев в своем алгоритме.
Некоторое время назад была также японская газета, которая утверждала, что у нее есть другой подход к разрешению этих ситуаций, начиная с триангуляции Делоне и вырабатывая из нее клетки вороной, но она тоже была ошибочной. Должно быть, приятно быть исследователем, придумывая широкие линейки алгоритмов и позволяя научным сотрудникам беспокоиться о деталях...