Изменение дат начала графиков для оптимизации ресурсов

Question

У меня есть куча работы, которую нужно выполнять через определенные промежутки времени. Однако у нас ограниченные ресурсы для выполнения этой работы каждый день. Поэтому я пытаюсь оптимизировать даты начала (даты начала можно перемещать только вперед, а не назад), чтобы повседневные ресурсы были в большей степени похожи на те, на которые мы заложили средства.

Эти функции используются в примере ниже:

# Function to shift/rotate a vector
shifter <- function(x, n = 1) {
  if (n == 0) x else c(tail(x, -n), head(x, n))
}

# Getting a range of dates
get_date_range <- function(current_date = Sys.Date(), next_planned_date = Sys.Date() + 5)
{
  seq.Date(as.Date(current_date), as.Date(next_planned_date), "days")
}

Предположим, что пример набора данных игрушек:: Здесь задача P1 начинается 14-го числа, а P2 - 15-го. Значение "ноль" означает, что в этот день для этой задачи не выполняется никакой работы.

# EXAMPLE TOY DATASET 
datain = data.frame(dated = c("2018-12-14", "2018-12-15", "2018-12-16", "2018-12-17"), 
                    P1 = c(1,2,0,3), P2 = c(0,4,0,6)) %>%
  mutate(dated = as.character(dated)) 

#The amount of resources that can be  used in a day
max_work = 4

# We will use all the possible combination of start dates to 
# search for the best one
possible_start_dates <- do.call(expand.grid, date_range_of_all)

# Utilisation stores the capacity used during each 
# combination of start dates
# We will use the minimum of thse utilisation
utilisation <- NULL # utilisation difference; absolute value
utilisation_act <-  NULL # actual utilisation including negative utilisation

# copy of data for making changes
ndatain <- datain
# Move data across possible start dates and 
# calculate the possible utilisation in each movements
for(i in 1:nrow(possible_start_dates)) # for every combination
{
  for(j in 1:ncol(possible_start_dates)) # for every plan
  {
    # Number of days that are different
    days_diff = difftime(oriz_start_date[["Plan_Start_Date"]][j], 
                         possible_start_dates[i,j], tz = "UTC", units = "days" ) %>% as.numeric()
    # Move the start dates
    ndatain[, (j+1)] <- shifter(datain[, (j+1)], days_diff)
  }
  if(is.null(utilisation)) # first iteration
  {
    # calculate the utilisation
    utilisation = c(i, abs(max_work - rowSums(ndatain %>% select(-dated))))
    utilisation_act <- c(i, max_work - rowSums(ndatain %>% select(-dated)))
  }else{ # everything except first iteration
    utilisation = rbind(utilisation, c(i,abs(max_work - rowSums(ndatain %>% select(-dated)))))
    utilisation_act <- rbind(utilisation_act, c(i, max_work - rowSums(ndatain %>% select(-dated))))

  }
}

# convert matrix to dataframe 
row.names(utilisation) <-  paste0("Row", 1:nrow(utilisation))
utilisation <- as.data.frame(utilisation)

row.names(utilisation_act) <-  paste0("Row", 1:nrow(utilisation_act))
utilisation_act <- as.data.frame(utilisation_act)

# Total utilisation
tot_util = rowSums(utilisation[-1])

# replace negative utilisation with zero
utilisation_act[utilisation_act < 0]  <- 0
tot_util_act = rowSums(utilisation_act[-1])

# Index of all possible start dates producing minimum utilization changes
indx_min_all = which(min(tot_util) == tot_util)
indx_min_all_act = which(min(tot_util_act) == tot_util_act)

# The minimum possible dates that are minimum of actual utilisation
candidate_dates <- possible_start_dates[intersect(indx_min_all, indx_min_all_act), ]

# Now check which of them are closest to the current starting dates; so that the movement is not much
time_diff <- c()
for(i in 1:nrow(candidate_dates))
{
  # we will add this value in inner loop so here we 
  timediff_indv <- 0
  for(j in 1:ncol(candidate_dates))
  {
    diff_days <- difftime(oriz_start_date[["Plan_Start_Date"]][j], 
                          candidate_dates[i,j], tz = "UTC", units = "days" ) %>% as.numeric()
    # print(oriz_start_date[["Plan_Start_Date"]][j])
    # print(candidate_dates[i,j])
    # 
    # print(diff_days)

    timediff_indv <- timediff_indv + diff_days
  }
  time_diff <- c(time_diff, timediff_indv)
}


# Alternatives
fin_dates  <-  candidate_dates[min(time_diff) == time_diff, ]

Приведенный выше код работает хорошо и выдает ожидаемый результат; однако это не хорошо масштабируется. У меня очень большой набор данных (за два года работы и более тысячи различных задач, повторяющихся с интервалами), и поиск по каждой возможной комбинации не является жизнеспособным вариантом. Есть ли способы, которыми я могу сформулировать эту проблему как стандартную проблему оптимизации и использовать Rglpk или же Rcplex или какое-то еще лучшее решение. Спасибо за вклад.

Answer 1

Вот мой самый длинный ответ на Stackru, но мне действительно нравятся проблемы с оптимизацией. Это вариант так называемой проблемы с магазином вакансий с одной машиной, которую вы могли бы решить с помощью Rcplex если вы впервые сформулируете это как LP-модель. Однако эти составы часто плохо масштабируются, и время вычислений может расти в геометрической прогрессии, в зависимости от состава. Для больших проблем очень распространено использование эвристики, например, генетического алгоритма, который я часто использую в подобных случаях. Это не гарантирует оптимального решения, но дает нам больший контроль над производительностью по сравнению со временем выполнения, и решение обычно очень хорошо масштабируется. По сути, он работает путем создания большого набора случайных решений, называемых популяцией. Затем мы итеративно обновляем эту совокупность, комбинируя решения для создания "потомства", где лучшие решения должны иметь более высокую вероятность создания потомства.

В качестве функции оценки (чтобы определить, какие решения "лучше"), я использовал сумму квадратов избыточной мощности в день, которая наказывает очень большую избыточную емкость в день. Обратите внимание, что вы можете использовать любую функцию подсчета очков, которую захотите, поэтому вы можете также штрафовать за недостаточное использование емкости, если считаете это важным.

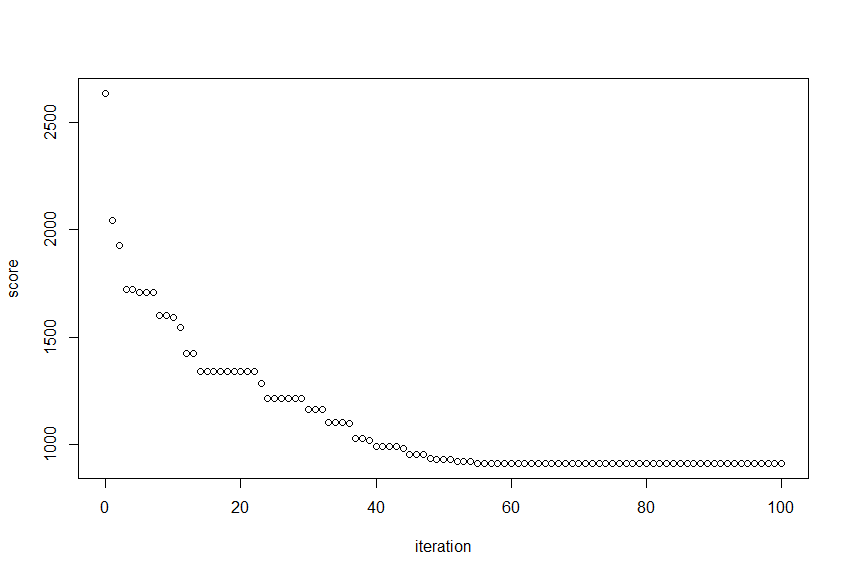
Код для примера реализации показан ниже. Я сгенерировал некоторые данные 200 дни и 80 задачи. Это работает около 10 секунд на моем ноутбуке, улучшив счет случайного решения более чем 65% от 2634 в 913, С вводом 700 дни и 1000 задач, алгоритм по-прежнему работает в течение нескольких минут с теми же параметрами.

Лучший результат решения за итерацию:

Я также включил use_your_own_sample_data, который вы можете установить TRUE чтобы алгоритм решил более простой и меньший пример, чтобы подтвердить, что он дает ожидаемый результат:

     dated P1 P2 P3 P4 P5                dated P1 P2 P3 P4 P5
2018-12-14  0  0  0  0  0           2018-12-14  0  0  3  1  0
2018-12-15  0  0  0  0  0           2018-12-15  0  3  0  0  1
2018-12-16  0  0  0  0  0   ---->   2018-12-16  0  0  3  1  0
2018-12-17  0  3  3  1  1           2018-12-17  0  3  0  0  1
2018-12-18  4  0  0  0  0           2018-12-18  4  0  0  0  0
2018-12-19  4  3  3  1  1           2018-12-19  4  0  0  0  0

Надеюсь, это поможет! Дайте мне знать, если у вас есть еще вопросы по этому поводу.

КОД

### PARAMETERS -------------------------------------------

n_population = 100 # the number of solutions in a population
n_iterations = 100 # The number of iterations
n_offspring_per_iter = 80 # number of offspring to create per iteration
max_shift_days = 20 # Maximum number of days we can shift a task forward
frac_perm_init = 0.25 # fraction of columns to change from default solution while creating initial solutions
early_stopping_rounds = 100 # Stop if score not improved for this amount of iterations
capacity_per_day = 4

use_your_own_sample_data = FALSE # set to TRUE to use your own test case


### SAMPLE DATA -------------------------------------------------
# datain should contain the following columns:
# dated: A column with sequential dates
# P1, P2, ...: columns with values for workload of task x per date

n_days = 200
n_tasks = 80

set.seed(1)
if(!use_your_own_sample_data)
{
  # my sample data:
  datain = data.frame(dated = seq(Sys.Date()-n_days,Sys.Date(),1))
  # add some random tasks
  for(i in 1:n_tasks)
  {
    datain[[paste0('P',i)]] = rep(0,nrow(datain))
    rand_start = sample(seq(1,nrow(datain)-5),1)
    datain[[paste0('P',i)]][seq(rand_start,rand_start+4)] = sample(0:5,5,replace = T)
  }
}  else 
{
  # your sample data:
  library(dplyr)
  datain = data.frame(dated = c("2018-12-14", "2018-12-15", "2018-12-16", "2018-12-17","2018-12-18","2018-12-19"), 
                      P1 = c(0,0,0,0,4,4), P2 = c(0,0,0,3,0,3), P3=c(0,0,0,3,0,3), P4=c(0,0,0,1,0,1),P5=c(0,0,0,1,0,1)) %>%
    mutate(dated = as.Date(dated,format='%Y-%m-%d')) 
}
tasks = setdiff(colnames(datain),c("dated","capacity")) # a list of all tasks
# the following vector contains for each task its maximum start date
max_date_per_task = lapply(datain[,tasks],function(x) datain$dated[which(x>0)[1]])



### ALL OUR PREDEFINED FUNCTIONS ----------------------------------

# helper function to shift a task
shifter <- function(x, n = 1) {
  if (n == 0) x else c(tail(x, n), head(x, -n))
}

# Score a solution
# We calculate the score by taking the sum of the squares of our overcapacity (so we punish very large overcapacity on a day)
score_solution <- function(solution,tasks,capacity_per_day)
{
  cap_left = capacity_per_day-rowSums(solution[,tasks]) # calculate spare capacity
  over_capacity = sum(cap_left[cap_left<0]^2) # sum of squares of overcapacity (negatives)
  return(over_capacity)
}

# Merge solutions
# Get approx. 50% of tasks from solution1, and the remaining tasks from solution 2.
merge_solutions <- function(solution1,solution2,tasks)
{
  tasks_from_solution_1 = sample(tasks,round(length(tasks)/2))
  tasks_from_solution_2 = setdiff(tasks,tasks_from_solution_1)
  new_solution = cbind(solution1[,'dated',drop=F],solution1[,tasks_from_solution_1,drop=F],solution2[,tasks_from_solution_2,drop=F])
  return(new_solution)
}

# Randomize solution
# Create an initial solution
randomize_solution <- function(solution,max_date_per_task,tasks,tasks_to_change=1/8)
{
  # select some tasks to reschedule
  tasks_to_change = max(1, round(length(tasks)*tasks_to_change))
  selected_tasks <- sample(tasks,tasks_to_change)
  for(task in selected_tasks)
  {
    # shift task between 14 and 0 days forward
    new_start_date <- sample(seq(max_date_per_task[[task]]-max_shift_days,max_date_per_task[[task]],by='day'),1)
    new_start_date <- max(new_start_date,min(solution$dated))
    solution[,task] = shifter(solution[,task],as.numeric(new_start_date-max_date_per_task[[task]]))
  }
  return(solution)
}

# sort population based on scores
sort_pop <- function(population)
{
  return(population[order(sapply(population,function(x) {x[['score']]}),decreasing = F)])
}

# return the scores of a population
pop_scores <- function(population)
{
  sapply(population,function(x) {x[['score']]})
}



### RUN SCRIPT -------------------------------

# starting score
print(paste0('Starting score: ',score_solution(datain,tasks,capacity_per_day)))

# Create initial population
population = vector('list',n_population)
for(i in 1:n_population)
{
  # create initial solutions by making changes to the initial solution 
  solution = randomize_solution(datain,max_date_per_task,tasks,frac_perm_init)
  score = score_solution(solution,tasks,capacity_per_day)
  population[[i]] = list('solution' = solution,'score'= score)
}

population = sort_pop(population)

score_per_iteration <- score_solution(datain,tasks,capacity_per_day)
# Run the algorithm
for(i in 1:n_iterations)
{
  print(paste0('\n---- Iteration',i,' -----\n'))

  # create some random perturbations in the population
  for(j in 1:10)
  {
    sol_to_change = sample(2:n_population,1)
    new_solution <- randomize_solution(population[[sol_to_change]][['solution']],max_date_per_task,tasks)
    new_score <- score_solution(new_solution,tasks,capacity_per_day)
    population[[sol_to_change]] <- list('solution' = new_solution,'score'= new_score)
  }

  # Create offspring, first determine which solutions to combine
  # determine the probability that a solution will be selected to create offspring (some smoothing)
  probs = sapply(population,function(x) {x[['score']]})
  if(max(probs)==min(probs)){stop('No diversity in population left')}
  probs = 1-(probs-min(probs))/(max(probs)-min(probs))+0.2
  # create combinations
  solutions_to_combine = lapply(1:n_offspring_per_iter, function(y){
    sample(seq(length(population)),2,prob = probs)})
  for(j in 1:n_offspring_per_iter)
  {
    new_solution <- merge_solutions(population[[solutions_to_combine[[j]][1]]][['solution']],
                                    population[[solutions_to_combine[[j]][2]]][['solution']],
                                    tasks)
    new_score <- score_solution(new_solution,tasks,capacity_per_day)
    population[[length(population)+1]] <- list('solution' = new_solution,'score'= new_score)
  }
  population = sort_pop(population)
  population= population[1:n_population]
  print(paste0('Best score:',population[[1]]['score']))
  score_per_iteration = c(score_per_iteration,population[[1]]['score'])
  if(i>early_stopping_rounds+1)
  {
    if(score_per_iteration[[i]] == score_per_iteration[[i-10]])
    {
      stop(paste0("Score not improved in the past ",early_stopping_rounds," rounds. Halting algorithm."))
    }
  }
}

plot(x=seq(0,length(score_per_iteration)-1),y=score_per_iteration,xlab = 'iteration',ylab='score')
final_solution = population[[1]][['solution']]
final_solution[,c('dated',tasks)]

---

И действительно, как мы и ожидали, алгоритм оказался очень хорошим в сокращении количества дней с очень высокой избыточностью:

final_solution = population[[1]][['solution']]

# number of days with workload higher than 10 in initial solution
sum(rowSums(datain[,tasks])>10)
> 19

# number of days with workload higher than 10 in our solution
sum(rowSums(final_solution[,tasks])>10)
> 1