Граница Парето (набор): порядок алгоритма

Question

Я должен выполнить задачу, которая включает в себя разработку алгоритма для вычисления границы Парето (множества). Заявление в основном:

Учитывая набор S из n точек в квадрате [0,1] x [0,1], составьте алгоритм для определения подмножества P, содержащегося в S, образованного недоминируемыми точками S.

Также говорят, что легко разработать алгоритм сравнения точек порядка n * n , который достигает этой цели. Ну, я придумал алгоритм, исследуя здесь и там. Задача по-прежнему состоит в том, чтобы реализовать алгоритм порядка n*log(n) . Как мне получить порядок этих алгоритмов?

Заранее спасибо!

      #data
set.seed(103)
x = runif(200)
y = runif(200)

#algorithm
pareto = 1:length(x)
for(i in 1:length(x)){
    cond1 = y[i]!=min(y[which(x==x[i])])
    cond2 = x[i]!=min(x[which(y==y[i])])
    for(k in 1:length(x)){
        if((x[i]>x[k]  &  y[i]>y[k]) | (x[i]==x[k] & cond1) | (y[i]==y[k] & cond2)){
            pareto[i] = NA
            break
        }
    }
}
xPareto = x[pareto[!is.na(pareto)]]
yPareto = y[pareto[!is.na(pareto)]]

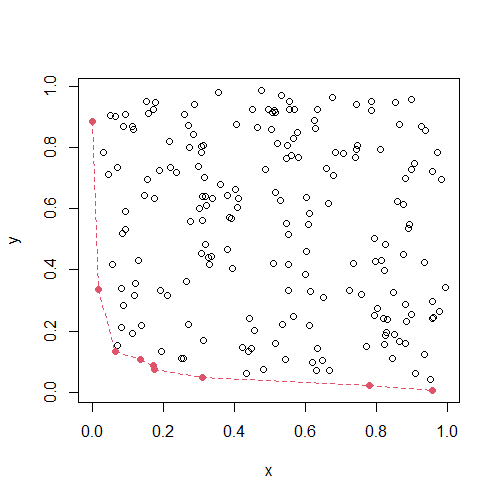
#graphic:
plot(x, y)
points(xPareto, yPareto, col=2, pch=16)
dat = data.frame(x=xPareto, y=yPareto)
dat = dat[order(dat$x),]
for(i in 1:(nrow(dat)-1)){
    segments(dat$x[i], dat$y[i], dat$x[i+1], dat$y[i+1], col=2, lty=2)
}

Answer 1

Интуиция, стоящая за эффективным жадным решением этой задачи, заключается в том факте, что точка доминирует над точкой тогда и только тогда, когда x[i] > x[j] а также y[i] > y[j], что означает, что это должно быть раньше, когда точки упорядочены по любой координате. Следовательно, если мы проходим точки в порядке возрастания их координат x, то точка (если есть), которая доминирует над точкой, должна быть пройдена до того , как точка пройдена. Другими словами, доминирующая точка не может идти после доминирующей точки в этом порядке.

Таким образом, с этим порядком обхода проблема доминирования (т. е. проверка того, доминирует ли точка над какой-либо другой точкой) сводится к проверке, видели ли мы уже точку с более низкой координатой y, поскольку порядок обхода уже обеспечивает выполнение условия координаты x . Это можно легко сделать, сверив координату y каждой точки с наименьшей (минимальной) координатой y, которую мы видели до сих пор — если минимальная координата y меньше, чем координата y текущей точки, то точка с минимальная координата y доминирует как x[j] < x[i]потому что jбыл замечен раньше i.

Сортировка по координате x требует времени, а проверка каждой точки (с сохранением частичного минимума координаты y) занимает O(n)время, в результате чего весь алгоритм занимает O(n log n)время.

      o = order(x)
minY = Inf

pareto = 1:n
for(j in 1:n){
    i = o[j]
    if (y[i] <= minY) {
        # Part of pareto boundary
        minY = y[i]
    } else {
        # Dominated by some point in pareto boundary
        pareto[i] = NA
    }
}